65537-gono para niños
Datos para niños 65537-gono |
||
|---|---|---|
 Un 65537-gono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 65 537 | |
| Vértices | 65 537 | |
| Grupo de simetría | Diedral (D65537), orden 2×65537 | |
| Símbolo de Schläfli | {65537} (65537-gono regular) | |
| Diagrama de Coxeter-Dynkin |       |
|
| Polígono dual | Autodual | |
| Área | 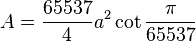 (lado  ) |
|
| Ángulo interior | 179.994507° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un 65537-gono es una figura plana con 65 537 lados rectos y 65 537 vértices (puntos donde se unen los lados). Este número, 65 537, es especial porque es un número de Fermat. Esto significa que tiene una propiedad muy interesante: ¡se puede dibujar usando solo una regla y un compás!
La suma de los ángulos interiores de un 65537-gono que no se cruza a sí mismo es de 11 796 300 grados.
Contenido
¿Qué es un 65537-gono regular?
Un 65537-gono regular es un tipo de polígono regular. Esto significa que todos sus 65 537 lados tienen la misma longitud. También, todos sus 65 537 ángulos interiores son iguales.
¿Cómo se ve un 65537-gono regular?
Aunque tiene lados rectos, un 65537-gono regular es tan grande y tiene tantos lados que, si lo dibujaras, ¡sería casi imposible distinguirlo de un círculo! Visualmente, se vería como un círculo perfecto. Su perímetro (la medida de su contorno) es casi idéntico al de un círculo que lo rodea.
¿Cómo se puede construir un 65537-gono?
La característica más sorprendente del 65537-gono regular es que es un polígono construible. Esto significa que se puede dibujar de forma precisa usando solo una regla (sin marcas) y un compás.
¿Por qué es construible este polígono?
La razón por la que se puede construir es que 65 537 es un número de Fermat. Los números de Fermat son números especiales que se pueden escribir de una forma particular: 2 elevado a (2 elevado a 'n'), más 1. En el caso de 65 537, 'n' es 4.
El famoso matemático Carl Friedrich Gauss ya sabía en 1801 que este polígono era construible. Sin embargo, la primera persona en mostrar cómo construirlo paso a paso fue Johann Gustav Hermes en 1894. Su trabajo fue increíblemente detallado y complejo. Hermes dedicó 10 años a escribir un manuscrito de 200 páginas explicando cómo hacerlo.
Un método más moderno para construirlo implica usar muchos "círculos de Carlyle". Estos círculos son herramientas geométricas que ayudan a resolver ciertos problemas matemáticos.
Simetría de un 65537-gono
Un 65537-gono regular tiene una simetría muy alta. Su simetría se llama "diedral Dih65537". Esto significa que si lo giras o lo volteas de ciertas maneras, se verá exactamente igual. Como 65 537 es un número primo, tiene varias formas de simetría más simples dentro de su estructura.
65537-grama: Una estrella de muchos picos
Un 65537-grama es una estrella que también tiene 65 537 lados. Imagina una estrella con muchísimos picos. Como 65 537 es un número primo, existen muchísimas formas diferentes de dibujar estas estrellas, cada una con un patrón único de conexión entre sus vértices.
Otros polígonos interesantes
- Triángulo equilátero (3 lados)
- Pentágono (5 lados)
- Heptadecágono (17 lados)
- 257-gono (257 lados)
Galería de imágenes
-
Las primeras etapas de la construcción de un 65537-gono regular usando círculos de Carlyle.
Véase también
En inglés: Regular polygon Facts for Kids
