Número de Fermat para niños
Datos para niños Primo de Fermat |
||
|---|---|---|
| Nombrado por | Pierre de Fermat | |
| No. de términos conocidos | 5 | |
| No. conjeturado de términos | 5 | |
| Subsecuencia de | Números de Fermat | |
| Primeros términos | 3, 5, 17, 257, 65537 | |
| Mayor término conocido | 65537 | |
| índice OEIS |
|
|
Un número de Fermat es un tipo especial de número natural. Reciben su nombre en honor a Pierre de Fermat, un famoso matemático francés. Estos números se calculan con una fórmula muy particular: 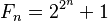 .
.
Aquí, la letra n representa un número natural (0, 1, 2, 3, y así sucesivamente). Los números de Fermat que también son números primos son especialmente interesantes y se llaman números primos de Fermat.
Contenido
La Conjetura de Fermat y el Descubrimiento de Euler
¿Qué Pensó Fermat sobre estos Números?
Pierre de Fermat estudió estos números y pensó que todos ellos serían números primos. Un número primo es aquel que solo se puede dividir por 1 y por sí mismo (como 3, 5, 7, 11, etc.).
Los primeros cinco números de Fermat son:
- Para n=0: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_{0} = 2^{2^0} + 1 = 2^1 + 1 = 3 (que es primo)
- Para n=1: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_{1} = 2^{2^1} + 1 = 2^2 + 1 = 5 (que es primo)
- Para n=2: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_{2} = 2^{2^2} + 1 = 2^4 + 1 = 17 (que es primo)
- Para n=3: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_{3} = 2^{2^3} + 1 = 2^8 + 1 = 257 (que es primo)
- Para n=4: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_{4} = 2^{2^4} + 1 = 2^{16} + 1 = 65537 (que es primo)
Como puedes ver, los primeros cinco números de Fermat son primos. Esto hizo que Fermat creyera que todos los números que se obtuvieran con su fórmula serían primos.
La Sorpresa de Euler
Sin embargo, en 1732, otro gran matemático llamado Leonhard Euler demostró que Fermat estaba equivocado. Euler calculó el sexto número de Fermat, cuando n=5: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_{5} = 2^{2^5} + 1 = 2^{32} + 1
Este número es 4.294.967.297. Euler descubrió que este número no es primo, sino que se puede dividir en 641 multiplicado por 6.700.417. Esto significa que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F_{5} es un número compuesto (un número que tiene más de dos divisores). Es el número de Fermat más pequeño que no es primo.
¿Cuántos Primos de Fermat Conocemos?
Hasta ahora, solo se conocen cinco números primos de Fermat. Son los mismos que ya conocía el propio Fermat: 3, 5, 17, 257 y 65537.
Los matemáticos aún tienen algunas preguntas sin respuesta sobre estos números:
- ¿Existen más números primos de Fermat además de los cinco que ya conocemos?
- ¿O son esos cinco los únicos que hay?
Estas son algunas de las preguntas sin resolver en el mundo de las matemáticas.
Ejemplos de Números de Fermat
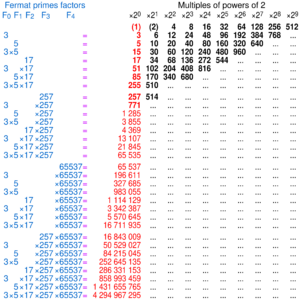
Aquí te mostramos los primeros números de Fermat y cómo se factorizan (si no son primos):
- F0 = 3 (es primo)
- F1 = 5 (es primo)
- F2 = 17 (es primo)
- F3 = 257 (es primo)
- F4 = 65.537 (es primo)
- F5 = 4.294.967.297 = 641 × 6.700.417 (es compuesto)
Como puedes ver, los números de Fermat crecen muy, muy rápido.
Propiedades Interesantes de los Números de Fermat
Relación entre Números de Fermat
Una propiedad curiosa es que cualquier número de Fermat es igual al producto de todos los números de Fermat anteriores, más 2. Por ejemplo:
- F1 = F0 + 2 (5 = 3 + 2)
- F2 = F0 × F1 + 2 (17 = 3 × 5 + 2)
- F3 = F0 × F1 × F2 + 2 (257 = 3 × 5 × 17 + 2)
Primos entre Sí
Dos números de Fermat diferentes siempre son primos entre sí. Esto significa que no tienen ningún factor común aparte del 1. Por ejemplo, F2 (17) y F3 (257) no comparten ningún divisor común. Esta propiedad es importante porque ayuda a demostrar que existen infinitos números primos.
Polígonos Construibles
El matemático Carl Friedrich Gauss descubrió una conexión fascinante entre los números primos de Fermat y la construcción de polígonos regulares usando solo una regla y compás.
El Teorema de Gauss-Wantzel dice que puedes construir un polígono regular de n lados con regla y compás si n es una potencia de 2 (como 2, 4, 8, 16...) o si n es el producto de una potencia de 2 y diferentes números primos de Fermat.
Por ejemplo:
- Un polígono de 3 lados (triángulo) se puede construir porque 3 es un primo de Fermat (F0).
- Un polígono de 5 lados (pentágono) se puede construir porque 5 es un primo de Fermat (F1).
- Un polígono de 17 lados se puede construir porque 17 es un primo de Fermat (F2).
- Un polígono de 15 lados (3 × 5) se puede construir porque 3 y 5 son primos de Fermat.
- Un polígono de 7 lados no se puede construir con regla y compás porque 7 no es un primo de Fermat ni un producto de ellos.
Aplicaciones de los Números de Fermat
Generación de Números Aleatorios en Computadoras
Los números primos de Fermat son útiles en la informática para crear secuencias de números que parecen aleatorios, llamadas números pseudoaleatorios. Esto es importante para muchas aplicaciones, como los videojuegos o la simulación de eventos.
Cuando las computadoras necesitan generar números "aleatorios" dentro de un rango específico (por ejemplo, de 1 a 256), pueden usar un método que involucra un número primo de Fermat. Esto es especialmente útil porque muchos datos en las computadoras se almacenan en bloques que son potencias de 2 (como un byte, que tiene 256 valores posibles).
Este método ayuda a que los números generados se distribuyan de manera uniforme, aunque no son verdaderamente aleatorios, ya que la secuencia se repite después de un tiempo.
Véase también
 En inglés: Fermat number Facts for Kids
En inglés: Fermat number Facts for Kids