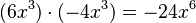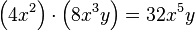Monomio para niños
En matemática, un monomio es una expresión algebraica que tiene un solo término. Imagina que es como una pieza de construcción en el mundo de las matemáticas. Está formado por números y letras que se multiplican entre sí.
Por ejemplo: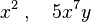 
Las letras en un monomio se llaman variables y pueden representar cualquier número. Los números pequeños que aparecen arriba de las letras (como el 2 en x²) se llaman exponentes y nos dicen cuántas veces se multiplica la letra por sí misma. En un monomio, los exponentes siempre son números naturales (1, 2, 3, etc.).
Cuando sumamos o restamos varios monomios, formamos algo más grande llamado polinomio. Un monomio es, de hecho, el tipo más simple de polinomio, ¡uno que solo tiene un término!
Contenido
¿Qué partes tiene un monomio?
Cada monomio tiene partes específicas que lo hacen único. Vamos a verlas con un ejemplo:
Dado el monomio: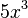 
Podemos identificar los siguientes elementos:
- Coeficiente: Es el número que acompaña a las letras. En este caso, es el 5. Este número también incluye el signo (si es negativo, como -5). Si no ves un número, el coeficiente es 1 (por ejemplo, en `x^2` el coeficiente es 1).
- Parte literal: Son las letras con sus exponentes. En nuestro ejemplo, es x³. Si no hay letras, se considera que la parte literal tiene un exponente cero, lo que hace que su valor sea 1.
- Grado: Es el exponente de la parte literal. En este caso, es el 3.
Si un monomio no tiene signo, se entiende que es positivo (+). El coeficiente nunca puede ser cero, porque si lo fuera, ¡todo el monomio valdría cero!
¿Qué es el grado de un monomio?
El grado de un monomio es la suma de todos los exponentes de sus letras. Nos dice qué tan "grande" es el monomio en términos de sus variables.
- El monomio
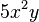tiene grado 3. Esto es porque `x` tiene un exponente de 2 y `y` tiene un exponente de 1 (cuando no se ve el exponente, es 1). Sumamos 2 + 1 = 3. - El monomio
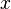tiene grado 1. Aquí, la `x` tiene un exponente de 1. - El monomio
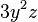tiene grado 3. Sumamos los exponentes de las letras: 2 (de `y`) + 1 (de `z`) = 3.
Monomios semejantes
Dos monomios son "semejantes" si tienen exactamente la misma parte literal, es decir, las mismas letras con los mismos exponentes. ¡No importa si sus coeficientes son diferentes!
Por ejemplo, estos monomios son semejantes: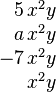 
Todos ellos tienen la parte literal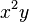 
.
Monomios heterogéneos
Los monomios heterogéneos son aquellos que no tienen el mismo grado absoluto. Por ejemplo:
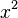(su grado es 2)
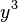(su grado es 3)
Como sus grados son diferentes, son monomios heterogéneos.
Operaciones con monomios
Podemos sumar, restar, multiplicar y dividir monomios, pero hay algunas reglas importantes.
Suma y resta de monomios
Solo podemos sumar o restar monomios que sean semejantes. Si no son semejantes, no se pueden combinar en un solo monomio.
Para sumarlos o restarlos, simplemente sumamos o restamos sus coeficientes y mantenemos la misma parte literal.
Ejemplo: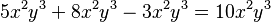 
Si los monomios no son semejantes, el resultado de la suma o resta será un polinomio (una expresión con varios términos).
Producto de monomios
Podemos multiplicar cualquier par de monomios. Para hacerlo, multiplicamos los coeficientes entre sí y luego multiplicamos las partes literales. Cuando multiplicamos letras iguales, sumamos sus exponentes.
Ejemplos:
(Multiplicamos 6 por -4 para obtener -24, y sumamos los exponentes de `x`: 3 + 3 = 6)
(Multiplicamos 4 por 8 para obtener 32. Sumamos los exponentes de `x`: 2 + 3 = 5. La `y` se mantiene igual).
Cociente de dos monomios
Para dividir dos monomios, dividimos los coeficientes y luego dividimos las partes literales. Cuando dividimos letras iguales, restamos sus exponentes. El resultado será un monomio solo si los exponentes de las letras en el resultado siguen siendo números naturales (o cero).
Ejemplo: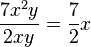 
(Dividimos 7 entre 2. Para `x`, restamos los exponentes: 2 - 1 = 1. Para `y`, restamos los exponentes: 1 - 1 = 0, y cualquier letra elevada a 0 es 1, así que la `y` desaparece).
Véase también
En inglés: Monomial Facts for Kids
