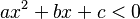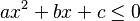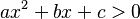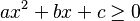Inecuación para niños
Una inecuación es como una balanza matemática que no está en equilibrio. En lugar de usar el signo de "igual" (=), que indica que ambos lados son exactamente lo mismo, las inecuaciones usan signos de desigualdad. Estos signos nos dicen si un lado es menor que (<), menor o igual que (≤), mayor que (>) o mayor o igual que (≥) el otro lado.
Por ejemplo, si ves la expresión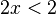 
, significa que "dos veces un número (x) es menor que dos". O 
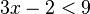significa "tres veces un número (x) menos dos es menor que nueve".
Las inecuaciones son verdaderas solo cuando los números que ponemos en lugar de las letras (variables) hacen que la desigualdad sea correcta.
Así como hay ecuaciones que siempre son ciertas (como 2=2) y otras que solo lo son para ciertos valores (como x+1=3, donde x debe ser 2), las inecuaciones también se dividen en dos tipos:
- Inecuaciones incondicionales: Son aquellas que son verdaderas para cualquier valor que le des a sus variables. Un ejemplo es
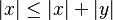. Esto significa que el valor absoluto de un número siempre es menor o igual que la suma de los valores absolutos de ese número y otro. - Inecuaciones condicionales: Son las que solo son verdaderas para algunos valores específicos de las variables. Por ejemplo, en
, solo algunos números para 'x' harán que la desigualdad sea cierta. Los números que hacen que la inecuación sea verdadera se llaman sus soluciones.
Contenido
Tipos de inecuaciones
Las inecuaciones se pueden clasificar de varias maneras, dependiendo de cuántas letras diferentes tengan o de la potencia más alta de esas letras.
Según el número de incógnitas
Las incógnitas son las letras (variables) que representan números desconocidos.
- De una incógnita: Solo tienen una letra, como
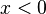. - De dos incógnitas: Tienen dos letras diferentes, como
. - De tres o más incógnitas: Pueden tener tres o más letras, como
.
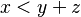Según la potencia de la incógnita
La potencia de una incógnita es el número pequeño que aparece arriba de la letra (exponente).
- De primer grado o lineales: La potencia más alta de la incógnita es uno. Por ejemplo:
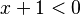. - De segundo grado o cuadráticas: La potencia más alta de cualquiera de sus incógnitas es dos. Por ejemplo:
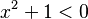. - De tercer grado o cúbicas: La potencia más alta de cualquiera de sus incógnitas es tres. Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^3 + 1 < 0 .
Inecuaciones de segundo grado con una incógnita
Estas inecuaciones tienen una sola letra y la potencia más alta de esa letra es dos. Se ven así (donde 'a', 'b' y 'c' son números, y 'a' no puede ser cero):
Sistemas de inecuaciones
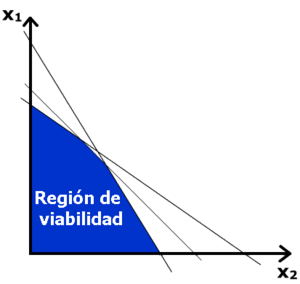
Un sistema de inecuaciones es cuando tienes dos o más inecuaciones que deben ser verdaderas al mismo tiempo. Imagina que tienes varias reglas y necesitas encontrar los números que cumplen con todas esas reglas a la vez. No todos los sistemas de inecuaciones tienen una solución.
Sistemas de inecuaciones de primer grado con una incógnita
Este tipo de sistema está formado por varias inecuaciones de primer grado. Por ejemplo: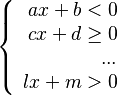 
La solución de un sistema de inecuaciones es el conjunto de todos los números que hacen que CADA inecuación del sistema sea verdadera al mismo tiempo.
Véase también
En inglés: Inequation Facts for Kids
- Ecuación
- Desigualdad matemática
- Sistema de ecuaciones
- Sistema de ecuaciones lineales
- Programación lineal
