Álgebra multilineal para niños

Enciclopedia para niños

La álgebra multilineal es una rama de las matemáticas que amplía las ideas del álgebra lineal. Se enfoca en el estudio de los productos tensoriales de espacios vectoriales y las transformaciones que trabajan con múltiples elementos a la vez.

Esta área de las matemáticas nos ayuda a entender objetos más complejos, como los tensores. Los tensores son como versiones avanzadas de los números simples (escalares) y las flechas con dirección (vectores). El álgebra multilineal es muy útil en campos como la física, la informática, la economía y el aprendizaje automático.

En la física, el álgebra multilineal es clave para estudiar los campos tensoriales. Estos campos describen propiedades físicas en el espacio y el tiempo, como las fuerzas internas en un material o los campos electromagnéticos. Por ejemplo, en la teoría de la relatividad, los tensores ayudan a describir cómo el espacio y el tiempo se curvan. También es importante en la mecánica cuántica para entender cómo interactúan muchas partículas.

En la informática, el álgebra multilineal es fundamental para el aprendizaje automático, especialmente en el aprendizaje profundo. Aquí, los tensores se usan para organizar grandes cantidades de datos en las redes neuronales. Las operaciones con tensores permiten encontrar patrones importantes en estos datos. Por ejemplo, las redes neuronales convolucionales (CNN) usan tensores para procesar y reconocer imágenes. También es vital en los gráficos por computadora para crear y manipular objetos en 3D.

En la economía, el álgebra multilineal se aplica en problemas de optimización. Ayuda a modelar decisiones en la teoría de juegos y a entender cómo se relacionan los diferentes sectores de una economía en los modelos de insumo-producto.

Las ciencias biológicas también se benefician. En la genómica, el álgebra multilineal ayuda a analizar grandes conjuntos de datos biológicos, como los niveles de actividad de los genes. En la biología de sistemas, estas técnicas permiten modelar redes complejas dentro de los seres vivos.

Contenido

¿Cómo surgió el álgebra multilineal?
¿Cómo se escribe el álgebra multilineal?
¿Qué es el producto tensorial?
Tensores y formas matemáticas
Uso en la topología algebraica
Aplicaciones importantes
- Física teórica
- Ingeniería
Conceptos relacionados
Galería de imágenes
Véase también

¿Cómo surgió el álgebra multilineal?

Aunque el álgebra lineal ya trabajaba con vectores simples, matemáticos como Hermann Grassmann comenzaron a pensar en estructuras más complejas. Él imaginó combinaciones de pares, tripletes y otros grupos de vectores, a los que llamó multivectores. Estas ideas expandieron el espacio de estudio a muchas más dimensiones.

El álgebra multilineal también ayuda a entender cómo los materiales responden a la fuerza y la deformación. El término "tensor" se usa para describir elementos en este espacio multilineal debido a su estructura especial. Aunque Grassmann publicó sus ideas en 1844, no fueron comprendidas de inmediato, ya que incluso el álgebra lineal era un desafío en esa época.

Los conceptos del álgebra multilineal se usan en el cálculo multivariante y en el estudio de las variedades. Por ejemplo, los pequeños cambios que se ven en el cálculo simple se convierten en formas diferenciales en el Cálculo multivariable, y se manejan con el álgebra exterior.

Después de Grassmann, otros matemáticos como Victor Schlegel y Elwin Bruno Christoffel continuaron desarrollando estas ideas. Gregorio Ricci-Curbastro y Tullio Levi-Civita hicieron avances importantes con el "cálculo diferencial absoluto". Más tarde, Marcel Grossmann y Michele Besso presentaron estas ideas a Albert Einstein. En 1915, Einstein usó el álgebra multilineal y los tensores en su teoría de la relatividad general, lo que demostró su gran importancia en la física.

En 1958, el grupo de matemáticos Nicolas Bourbaki incluyó un capítulo sobre álgebra multilineal en su serie de libros Éléments de mathématique. Este capítulo cubrió temas como las funciones bilineales y el producto tensorial.

¿Cómo se escribe el álgebra multilineal?

El álgebra multilineal usa una forma especial de escribir las cosas llamada notación multi-índice. Esto significa que se usan varios números pequeños (índices) para representar combinaciones de elementos.

Por ejemplo, un objeto simple llamado tensor de rango uno se escribe así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \scriptstyle X=X^se_s\, . Esto es una forma corta de decir que X es la suma de varios elementos:

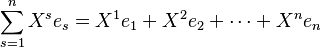
$\sum_{s=1}^{n}X^se_s=X^1e_1+X^2e_2+\cdots+X^ne_n$

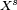Aquí, $\scriptstyle e_s\,$ son los "vectores básicos" y $\scriptstyle X^s\,$ son los "componentes" de X. La letra $n$ indica la dimensión del espacio.

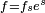También existen los "1-co tensores", que son funciones que transforman un espacio en números. Se escriben como $\scriptstyle f=f_se^s\,$ .

Los tensores de rango dos son más complejos:
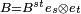- Un tensor de rango dos "contravariante" se escribe $\scriptstyle B=B^{st}e_s\otimes e_t$ .
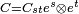- Un tensor de rango dos "covariante" se escribe $\scriptstyle C=C_{st}e^s\otimes e^t$ .
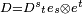- Un tensor de rango dos "mixto" se escribe $\scriptstyle D={D^s}_t e_s\otimes e^t$ .

Por ejemplo, si el espacio tiene dos dimensiones, un tensor B se vería así:

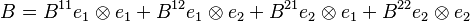
$B=B^{11}e_1\otimes e_1+B^{12}e_1\otimes e_2+B^{21}e_2\otimes e_1+B^{22}e_2\otimes e_2$

De forma general, para un tensor mixto A, se usa la notación 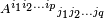$\scriptstyle {A^{i_1i_2...i_p}}_{j_1j_2...j_q}$ para sus componentes. La expresión completa es:

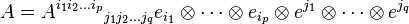
$A={A^{i_1i_2...i_p}}_{j_1j_2...j_q}e_{i_1}\otimes\cdots\otimes e_{i_p}\otimes e^{j_1}\otimes\cdots\otimes e^{j_q}$

Esta notación es una forma abreviada de representar sumas complejas.

Todo esto se aplica cuando el espacio vectorial tiene una dimensión finita, es decir, un número limitado de direcciones.

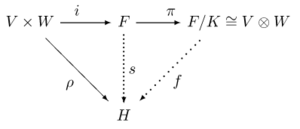
¿Qué es el producto tensorial?

El producto tensorial es una forma de combinar dos espacios vectoriales, digamos V y W, para crear un nuevo espacio. Si V tiene una base de elementos 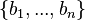$\{b_1,...,b_n\}$ y W tiene 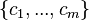$\{c_1,...,c_m\}$ , su producto tensorial Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V\otimes W es un espacio generado por nuevos símbolos como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b_i\otimes c_j .

Esto significa que cualquier objeto X que pertenezca a 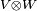$\scriptstyle V\otimes W$ se puede escribir como una combinación de estos nuevos símbolos:

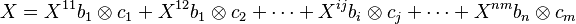
$X=X^{11}b_1\otimes c_1+X^{12}b_1\otimes c_2+\cdots+ X^{ij}b_i\otimes c_j+\cdots+X^{nm} b_n\otimes c_m$

Esta expresión se abrevia como 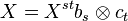$X=X^{st}b_s\otimes c_t$ . Cuando un índice se repite (uno arriba y uno abajo), significa que se está sumando sobre todos los posibles valores de ese índice.

Esta definición es muy abstracta, pero permite explorar muchas posibilidades. Al combinar un espacio vectorial V con su espacio dual 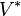$V^*$ (que es el espacio de funciones lineales), se obtienen otros espacios importantes como:

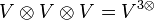
$V\otimes V\otimes V=V^{3\otimes}$

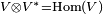
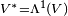
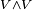
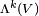
$\scriptstyle V\otimes V^*={\rm Hom}(V)$ $\scriptstyle V^*=\Lambda^1(V)\,$ $\scriptstyle V\wedge V$ $\scriptstyle \Lambda^k(V)\,$

Todos estos espacios se usan a diario en áreas avanzadas de las matemáticas y la física, como la geometría diferencial, la geometría algebraica, la relatividad y la cuántica.

Tensores y formas matemáticas

Consideremos un espacio V generado por elementos 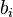$b_i$ . Su espacio dual 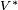$\scriptstyle V^*$ tiene una base 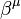$\beta^{\mu}$ . Cualquier elemento del espacio 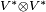$\scriptstyle V^*\otimes V^*$ se escribe como 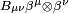$\scriptstyle B_{\mu\nu}\beta^{\mu}\otimes\beta^{\nu}$ . Esta expresión también puede verse como una función que toma dos elementos de V y produce un número real.

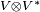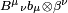Otro tipo de tensor de rango dos es $\scriptstyle V\otimes V^*$ . Sus elementos se ven como combinaciones de la forma $\scriptstyle {B^{\mu}}_\nu b_{\mu}\otimes \beta^{\nu}$ .

Uso en la topología algebraica

A mediados del siglo XX, los tensores se definieron de una manera más abstracta. El libro Álgebra multilineal del grupo Bourbaki fue muy importante y pudo haber dado origen al término "álgebra multilineal".

Una de las razones para este desarrollo fue una nueva área llamada álgebra homológica. El avance de la topología algebraica en la década de 1940 impulsó la necesidad de un tratamiento puramente algebraico del producto tensorial. Calcular los grupos de homología del producto de dos espacios topológicos implica el producto tensorial.

El objetivo era organizar una gran cantidad de ideas, incluyendo las de Hermann Grassmann, las formas diferenciales (que llevaron a la cohomología de De Rham) y conceptos más básicos como el producto de cuña.

La forma en que Bourbaki presentó el tema fue muy rigurosa. Rechazaron el enfoque del cálculo vectorial y, en su lugar, usaron un método basado en la teoría de categorías. Esto llevó a una explicación más clara y puramente matemática.

En esencia, el álgebra multilineal explica por qué los espacios tensoriales son las herramientas necesarias para transformar problemas complejos (multilineales) en problemas más sencillos (lineales). Este enfoque algebraico no se basa en la intuición geométrica, sino en propiedades matemáticas fundamentales.

Al usar el álgebra multilineal, se encuentra una "mejor solución" para los problemas. Las soluciones son precisas y no necesitan ideas adicionales o sistemas de coordenadas. En el lenguaje de la teoría de categorías, todo es "natural".

Aplicaciones importantes

Física teórica

En la física teórica, los tensores se usan para describir cantidades físicas como las fuerzas internas en los materiales, los campos electromagnéticos y la curvatura del espacio-tiempo en la Teoría General de la Relatividad.

Ingeniería

En las ciencias de la ingeniería, los tensores ayudan a describir las propiedades mecánicas de los materiales, el movimiento de los fluidos y otros fenómenos físicos.

Conceptos relacionados

Aquí hay algunos conceptos importantes que se desarrollan en el álgebra multilineal:

tensor
espacio dual
covector
geometría diferencial
cálculo tensorial
análisis vectorial
covariancia y contravariancia
tensor métrico
derivada covariante
conexión
tensor de curvatura de Riemann
símbolos de Christoffel
álgebra exterior
forma diferencial
curvatura
teorema de Stokes
Símbolo de Levi-Civita
Sección (matemática)
Campo vectorial
Campo tensorial
Pullback

Construcción de productos de tensores.

Galería de imágenes

Construcción de productos de tensores.

Véase también

En inglés: Multilinear algebra Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Álgebra_multilineal&oldid=4687739»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Álgebra multilineal para Niños. Enciclopedia Kiddle.