Teoría del caos para niños
La teoría del caos es una parte de las matemáticas, la física y otras ciencias, como la biología o la meteorología. Estudia sistemas complejos y dinámicos que son muy sensibles a pequeños cambios en sus condiciones iniciales.
Esto significa que una variación mínima al principio puede causar grandes diferencias en el futuro. Aunque estos sistemas son predecibles si se conocen sus condiciones iniciales, en la práctica es casi imposible predecirlos a largo plazo.
La teoría del caos nos ayuda a entender por qué algunos sistemas son tan difíciles de predecir. No solo se aplica a sistemas con muchos elementos, sino también a otros más sencillos.
El comportamiento caótico se ve en la naturaleza, como en el movimiento de los líquidos, el ritmo del corazón o el clima. También aparece en sistemas creados por el ser humano, como el tráfico. Esta teoría se usa en meteorología, informática, ingeniería y otras áreas.
Plantilla:Ficha de disciplina científica
Contenido
¿Cómo se clasifican los sistemas dinámicos?
Los sistemas dinámicos se pueden clasificar en tres tipos principales:
- Estables: Si dos soluciones empiezan cerca, se mantienen cerca con el tiempo. Un sistema estable tiende a un punto o a una órbita fija.
- Inestables: Si dos soluciones empiezan cerca, se separan mucho con el tiempo. Un sistema inestable se aleja de los puntos de atracción.
- Caóticos: No son inestables, pero sus soluciones, aunque se mantienen en una zona limitada, se mueven de forma irregular. Con el tiempo, dos soluciones cercanas se vuelven muy diferentes.
Una característica importante de los sistemas inestables y caóticos es que dependen mucho de las condiciones iniciales. Si conocemos las ecuaciones de un sistema y sus condiciones iniciales, podemos saber cómo evolucionará. Pero en los sistemas caóticos, un cambio mínimo al principio hace que la evolución sea totalmente distinta. Ejemplos son el Sistema Solar o el clima.
¿Qué es el caos determinista?
El caos determinista se refiere a fenómenos donde el movimiento parece aleatorio, pero en realidad está completamente determinado. Esto significa que, aunque podemos describir su comportamiento con reglas fijas, es casi imposible predecir su futuro.
¿Qué define el caos y los atractores?
Aunque no hay una definición única de caos, los científicos están de acuerdo en tres puntos clave:
- Movimiento oscilante: Las trayectorias no se quedan en un punto fijo ni se repiten de forma simple.
- Determinismo: El sistema no es aleatorio, sino que sigue reglas fijas. Su comportamiento irregular viene de su naturaleza no lineal.
- Sensibilidad a las condiciones: Trayectorias que empiezan muy cerca se separan rápidamente con el tiempo. Pequeñas diferencias iniciales llevan a resultados muy distintos.
Los sistemas caóticos suelen tener un "atractor". Un atractor es un conjunto de puntos hacia donde tienden todas las trayectorias cercanas. Hay tres características de los atractores:
- Cualquier trayectoria que esté en un atractor, permanecerá en él para siempre.
- Atraen a un grupo de condiciones iniciales.
- No hay condiciones iniciales que cumplan las dos reglas anteriores.
Un atractor se llama "extraño" o "caótico" si muestra una gran sensibilidad a las condiciones iniciales.
La importancia de la no linealidad
Hay dos tipos principales de sistemas dinámicos: las ecuaciones diferenciales (para el tiempo continuo) y los sistemas iterativos (para el tiempo discreto). Ambos son útiles para estudiar el caos.
Un sistema es no lineal cuando sus variables no tienen una potencia de uno, o cuando hay productos o funciones de las variables. Por ejemplo,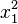 
o 
.
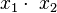La mayoría de los sistemas no lineales son difíciles de resolver de forma exacta. Se pueden hacer aproximaciones, pero se pierde precisión. Muchos fenómenos en la naturaleza son no lineales.
La importancia de los sistemas no lineales en el caos es que pequeños cambios en las condiciones iniciales pueden causar grandes cambios en el resultado final.
¿Por qué las trayectorias cercanas se separan?
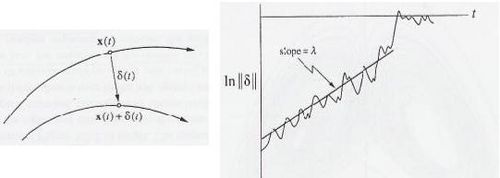
Los atractores caóticos son muy sensibles a las condiciones iniciales. Esto significa que dos trayectorias que empiezan muy cerca se separan rápidamente, y cada una tendrá un futuro muy diferente. Esta separación se puede medir con el exponente Lyapunov. Si este exponente es positivo, la predicción deja de ser válida después de un tiempo.
Aunque seamos muy precisos al medir las condiciones iniciales, el tiempo que podemos predecir no aumenta mucho. Por eso, Edward Lorenz dijo que era tan difícil predecir el tiempo. Este problema se conoce como el efecto mariposa. Lorenz lo explicó con la pregunta: ¿Puede el batir de las alas de una mariposa en Brasil dar lugar a un tornado en Texas?.
La sensibilidad es tan grande que se compara con la frase: "Por perder un clavo, el caballo perdió la herradura, el jinete perdió al caballo, el jinete no combatió, la batalla se perdió, y con ella perdimos el reino."
Si dibujamos la separación entre dos trayectorias a lo largo del tiempo, veremos que al principio aumenta rápidamente. Luego, como el atractor está limitado en un espacio, la distancia no puede crecer infinitamente.
Tipos de atractores
El movimiento de un sistema dinámico se puede ver en un diagrama de fases. Cuando el sistema tiende a un tipo de movimiento, decimos que hay un atractor.
Existen varios tipos de atractores:
- Atractor de punto fijo: El sistema tiende a estabilizarse en un solo punto. Un péndulo que se detiene por el roce con el aire es un ejemplo.
- Atractor de ciclo límite o atractor periódico: El sistema tiende a un movimiento que se repite en un ciclo fijo. Un péndulo que oscila sin parar (si se le da energía para compensar el roce) es un ejemplo.
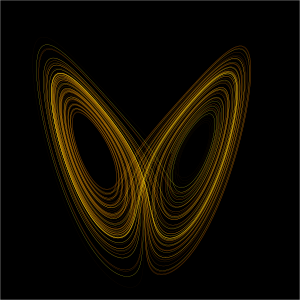
- Atractor caótico: Aparece en sistemas no lineales muy sensibles a las condiciones iniciales. El atractor de Lorenz es un ejemplo famoso.
Estos nombres describen el tipo de movimiento que causan en los sistemas. Un atractor periódico, por ejemplo, puede guiar el movimiento de un péndulo en oscilaciones regulares.
Ejemplos de atractores
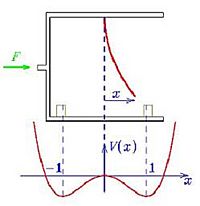
Un modelo matemático sencillo para explicar el caos es una varilla de acero que oscila entre dos imanes. La base de la varilla se mueve con una fuerza regular.
Cuando la varilla está vertical, hay un punto de equilibrio inestable entre dos puntos estables. Si añadimos el roce con el aire y una fuerza externa, obtenemos la ecuación de Duffing. El término no lineal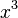 
en esta ecuación tiene efectos sorprendentes.
 |
 |
|
|
|
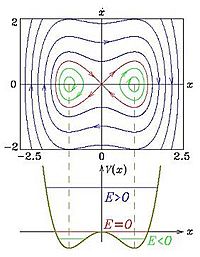
Si no hay roce ni fuerza externa, el sistema es conservador. Las trayectorias en el espacio de fases muestran oscilaciones periódicas.
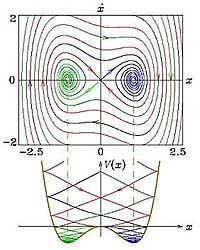
Si consideramos el roce, las oscilaciones se amortiguan y el sistema tiende a uno de los puntos fijos.
Si además del roce, añadimos una fuerza externa que lo contrarresta, el sistema ya no tiende al equilibrio. Se encuentran soluciones periódicas (ciclos límite) que dependen de la fuerza externa.
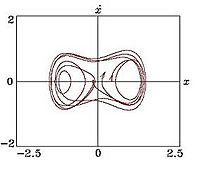
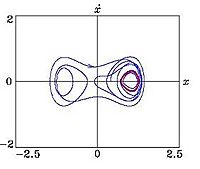
Pero si aumentamos la fuerza externa, las órbitas periódicas desaparecen y el sistema oscila sin regularidad. Además, muestra una gran sensibilidad a las condiciones iniciales, lo que indica un atractor caótico.
Para que haya caos en un sistema, se necesitan tres cosas:
- Debe ser no lineal.
- Debe tener al menos tres variables (o dos variables y no ser autónomo).
- Debe ser sensible a las condiciones iniciales.
 |
 |
|
|
|
En el modelo matemático, cuando 
, era no lineal. Al introducir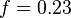 
, se añade una tercera variable (el tiempo). Es importante recordar que tener tres o más variables no siempre significa que habrá caos.
Una forma de ver el movimiento caótico es con un diagrama de fases. En este diagrama, el tiempo no se muestra directamente, y cada eje representa una parte del estado del sistema. Un sistema en reposo es un punto, y uno en movimiento periódico es un círculo.
Atractores extraños
Los atractores extraños son formas muy complejas en el espacio de fases. Describen el movimiento irregular de un sistema caótico. El atractor de Lorenz es un ejemplo famoso, con una forma parecida a las alas de una mariposa.
Estos atractores tienen una estructura de fractal, lo que significa que tienen patrones que se repiten a diferentes escalas.
Un teorema llamado teorema de Poincaré-Bendixson dice que un atractor extraño solo puede aparecer en sistemas continuos si tienen tres o más dimensiones. Sin embargo, en sistemas discretos, pueden aparecer en dos o incluso una dimensión.
Más sobre atractores
Los atractores extraños son curvas en el espacio de fases que muestran la trayectoria de un sistema caótico. Un sistema con estas características es impredecible; saber su estado en un momento no permite predecirlo con certeza más tarde. Sin embargo, el movimiento no es completamente aleatorio.
En la mayoría de los sistemas dinámicos, hay elementos que permiten un movimiento repetitivo. Los atractores hacen que las variables sigan una trayectoria establecida. Lo que no se puede predecir con exactitud son las pequeñas variaciones que las variables pueden tener al recorrer esas trayectorias. Por ejemplo, podemos prever la trayectoria de un satélite alrededor de la Tierra, pero no los pequeños movimientos o problemas que pueda tener.
La transformación del panadero
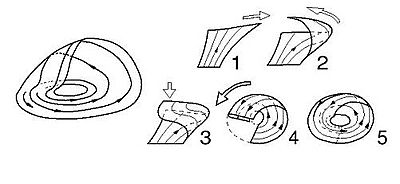
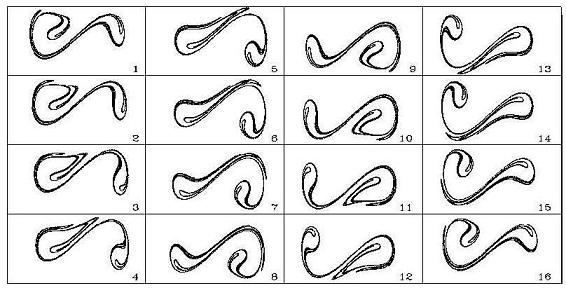
Los atractores extraños tienen órbitas irregulares, sus trayectorias se separan rápidamente y se mantienen en un espacio limitado. Para entender esto, se usa la "transformación del panadero". Consiste en un proceso doble de estirar y plegar.
Este proceso de estirar (para separar las trayectorias) y plegar (para mantenerlas en un espacio limitado) es clave en el caos determinista. Se llama "transformación del panadero" porque al amasar, se estira y se pliega la masa repetidas veces.
Al repetir este proceso infinitas veces, se forman infinitas capas, dando al atractor una estructura fractal. El atractor de Rössler es un ejemplo. En su gráfico, se ve cómo se estira y luego se pliega.
Otro ejemplo es la ecuación de Duffing. Como tiene una fuerza externa, su espacio de fases es tridimensional. Para verlo, se usan "secciones estroboscópicas" en momentos específicos.
Breve historia de la teoría del caos
El caos y los fractales son parte de la dinámica, una rama de la física que comenzó en el siglo XVII. Fue entonces cuando Isaac Newton descubrió las ecuaciones diferenciales, las leyes de movimiento y la gravitación universal. Newton pudo resolver problemas de dos cuerpos que interactúan por la gravedad. Sin embargo, el movimiento de la Luna y el problema de los tres cuerpos (cómo se mueven tres cuerpos que se atraen) eran mucho más difíciles.
El determinismo de Laplace
En 1776, el matemático francés Pierre Simon de Laplace publicó su obra Traité de Mécanique Céleste. Él afirmaba que si se conocieran la velocidad y la posición de todas las partículas del universo en un instante, se podría predecir su pasado y su futuro. Por más de 100 años, esta idea, conocida como determinismo laplaciano, parecía correcta.
El determinismo laplaciano decía que si conoces las leyes de un fenómeno, sus condiciones iniciales y puedes calcular la solución, entonces puedes predecir con total certeza el futuro del sistema.
Las preguntas de Poincaré
A finales del siglo XIX, Henri Poincaré (1854-1912), un matemático francés, empezó a cuestionar si el Sistema Solar sería estable para siempre. Poincaré fue el primero en pensar en la posibilidad del caos, es decir, un comportamiento que depende mucho de las condiciones iniciales. En 1903, Poincaré dijo:
El azar no es más que la medida de la ignorancia del hombre.
Reconoció que muchos fenómenos no eran completamente aleatorios, sino que pequeños cambios al principio llevaban a grandes cambios en el resultado.
Poincaré identificó propiedades que hacían imposible la predicción a largo plazo en sistemas como el clima, el flujo de la sangre en el corazón, las turbulencias, los atascos de vehículos y las epidemias.
La contribución de Lorenz
La historia reciente del caos comenzó en la década de 1950, con la invención de los ordenadores. Esto permitió estudiar el comportamiento de los sistemas no lineales de forma gráfica. En 1963, Edward Lorenz trabajaba con unas ecuaciones, las famosas ecuaciones de Lorenz, para predecir el tiempo en la atmósfera. Usó ordenadores para ver el comportamiento de sus ecuaciones.
Los ordenadores de esa época eran lentos. Lorenz dejó el suyo calculando y, al volver, encontró una figura que hoy se conoce como atractor de Lorenz. Pensó que había un error, pero al repetir el proceso, siempre obtenía el mismo resultado. Se dio cuenta de que algo especial pasaba con su sistema de ecuaciones simplificado.
Después de estudiar el problema, Lorenz concluyó que las simulaciones eran muy diferentes con condiciones iniciales muy parecidas. Recordó que su programa solo permitía introducir tres decimales para las condiciones iniciales, aunque el programa trabajaba con seis. Los últimos tres decimales se introducían al azar. Lorenz publicó sus descubrimientos en revistas de meteorología, pero pasaron desapercibidos por casi una década.
La década de 1970 fue el "auge del caos". En 1971, David Ruelle y Floris Takens propusieron una nueva teoría para la turbulencia de fluidos basada en un atractor extraño. Años después, Robert May encontró ejemplos de caos en la dinámica de poblaciones. Luego, Feigenbaum descubrió leyes universales que explican la transición entre el comportamiento regular y el caótico.
Ecuaciones de Lorenz
El primer sistema de ecuaciones que mostró un comportamiento caótico fue el propuesto por Lorenz:
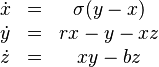
Aquí,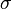 
es el número de Prandtl (relacionado con la viscosidad), 
es el número de Rayleigh (relacionado con la diferencia de temperatura) y 
es la relación entre la longitud y altura del sistema.
Lorenz notó dos cosas importantes en su ecuación:
- Cualquier diferencia, por pequeña que fuera, en las condiciones iniciales cambiaba drásticamente los resultados. Solo se podía predecir el sistema por periodos cortos. Esto llevó al efecto mariposa, la hipersensibilidad a las condiciones iniciales.
- A pesar de la impredecibilidad, el sistema tendía a evolucionar dentro de una zona muy específica del espacio de fases, como si tuviera un "pseudocentro de gravedad".
Las ecuaciones de Lorenz eran un modelo simplificado de la convección en la atmósfera terrestre. Las tres magnitudes en su sistema representan:
Velocidad de rotación del aire.
Diferencia de temperatura.
Desviación de la temperatura respecto a su valor normal.
Lorenz descubrió que su sistema tenía un comportamiento muy irregular. Las soluciones oscilaban sin repetirse, pero siempre dentro de una región limitada. Las trayectorias siempre rondaban lo que ahora se llama atractor extraño.
Aplicaciones de la teoría del caos
La teoría del caos y la teoría de sistemas dinámicos tienen muchas aplicaciones en ciencias naturales, tecnología y ciencias sociales. Se han usado para controlar, describir y modelar sistemas complejos. Desde los años 60, ha crecido mucho la investigación en este campo.
En el libro Teoría del Caos, el tercer paradigma, se explica cómo se usan modelos aleatorios para crear "series caóticas predictoras" y estudiar eventos que parecen caóticos en las ciencias sociales.
En meteorología: ¿Por qué es tan difícil predecir el tiempo?
El tiempo atmosférico es un sistema dinámico muy sensible a los cambios iniciales. Por eso, es adecuado para estudiarlo con la matemática caótica. La precisión de las predicciones meteorológicas es relativa.
A finales del siglo XX, se decía que las predicciones tenían una precisión de entre 80 y 85% para un día. Los modelos numéricos de la teoría del caos han mejorado mucho la exactitud de las previsiones, especialmente para periodos de más de un día. Hoy se pueden hacer predicciones fiables hasta por cinco días, y se han logrado algunos éxitos en predecir cambios anormales de temperatura y lluvia hasta por 30 días.
Antes de la teoría del caos, se pensaba que para predecir el tiempo con exactitud solo hacía falta introducir más variables en un ordenador potente. Sin embargo, aunque se han pasado de unas pocas variables a cientos de miles, no se ha logrado la predictibilidad esperada. El tiempo atmosférico, como sistema caótico, es impredecible a largo plazo, aunque sigue un cierto orden a través de las estaciones.
Se ha calculado que una predicción a dos meses vista requeriría conocer las condiciones iniciales con una precisión 100 mil veces mayor que la que se obtiene con la predicción. El clima, que es el promedio del tiempo atmosférico, no es tan sensible a las condiciones iniciales y no es caótico. Por lo tanto, la predicción del clima depende de conocer los factores que cambian la energía de la Tierra, no de una gran precisión en las medidas iniciales.
En economía: ¿Cómo se aplica el caos?
Es posible que los modelos económicos puedan mejorar con la teoría del caos. Sin embargo, predecir el estado de un sistema económico y qué factores influyen más es muy complejo.
Algunos dicen que los sistemas económicos y financieros son diferentes de los de las ciencias naturales. Son más bien aleatorios, ya que resultan de las interacciones de las personas. Por eso, los modelos puramente deterministas quizás no sean precisos. La investigación sobre el caos en economía y finanzas ha dado resultados variados.
El caos se puede encontrar en la economía usando el análisis de cuantificación de recurrencia. Por ejemplo, se han detectado cambios ocultos en series de tiempo económicas. Esta técnica también se ha usado para ver transiciones de fases regulares a caóticas y para entender mejor la dinámica económica. El caos podría ayudar a modelar la economía y a incluir eventos externos como el COVID-19.
En medicina: ¿Ayuda el caos a la salud?
El análisis de datos de electrocardiogramas y encefalogramas muestra detalles que parecen aleatorios. Sin embargo, estos datos parecen ser generados por un sistema caótico. Los parámetros matemáticos que describen estas series se han usado para diagnosticar algunas enfermedades. Esto permite un diagnóstico temprano de ciertas patologías.
Véase también
En inglés: Chaos theory Facts for Kids
- Oscilador de van der Pol
- Aleatoriedad
- Caos
- Fractal
- Dinámica de sistemas
- Problema de los tres cuerpos
- Problema de los n cuerpos
- Estabilidad del sistema solar
- Ilya Prigogine
- René Thom
