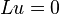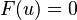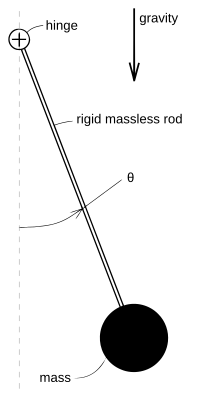Sistema no lineal para niños
Un sistema no lineal es un tipo de sistema en matemáticas, física o cualquier otra área, donde el resultado final no es simplemente la suma de sus partes. Imagina que tienes varios ingredientes para una receta; en un sistema lineal, si duplicas cada ingrediente, duplicas el resultado. Pero en un sistema no lineal, si duplicas los ingredientes, el resultado podría ser algo completamente diferente, no solo el doble.
En estos sistemas, las reglas o ecuaciones que describen su comportamiento no son "lineales". Esto significa que no siguen una línea recta o una proporción simple. Por eso, los sistemas no lineales pueden tener comportamientos muy complejos y, a menudo, difíciles de predecir. A veces, incluso un pequeño cambio al principio puede llevar a resultados muy diferentes más adelante, un fenómeno que se estudia en la teoría del caos.
La no linealidad es muy común en la naturaleza y en la tecnología. Por ejemplo, el clima, el movimiento de un péndulo o la forma en que se propagan las ondas de luz en ciertos materiales son ejemplos de sistemas no lineales. Gracias a las computadoras modernas, los científicos pueden estudiar estos sistemas complejos de maneras que antes eran imposibles.
Contenido
¿Qué son los Sistemas No Lineales?
Los sistemas no lineales son aquellos donde la relación entre la causa y el efecto no es directa ni proporcional. Esto significa que si cambias algo en el sistema, el resultado no será simplemente un cambio proporcional. Por ejemplo, si empujas un columpio un poco más fuerte, no necesariamente se moverá el doble de lejos. Su comportamiento es más complicado.
¿Cómo se diferencian de los Sistemas Lineales?
Para entender mejor los sistemas no lineales, es útil compararlos con los sistemas lineales.
Sistemas Lineales: Sencillos y Predecibles
Un sistema lineal es como una máquina simple donde la salida es directamente proporcional a la entrada. Si pones el doble de esfuerzo, obtienes el doble de resultado. En matemáticas, esto se conoce como el Principio de Superposición, que tiene dos reglas:
- Aditividad: Si sumas dos entradas, la salida es la suma de las salidas individuales.
- Homogeneidad: Si multiplicas una entrada por un número, la salida se multiplica por el mismo número.
Gracias a estas reglas, los sistemas lineales son fáciles de entender y predecir.
Sistemas No Lineales: Complejos y Sorprendentes
Los sistemas no lineales no siguen el Principio de Superposición. Esto los hace mucho más difíciles de analizar y predecir. Sus soluciones no se pueden simplemente "sumar" para obtener nuevas soluciones. Por esta razón, pueden mostrar fenómenos interesantes y a veces inesperados, como:
- Caos: Pequeños cambios iniciales pueden llevar a resultados muy diferentes a largo plazo.
- Solitones: Ondas que mantienen su forma mientras viajan.
- Singularidades: Puntos donde el comportamiento del sistema se vuelve extremo o indefinido.
¿Por qué son difíciles de estudiar?
Como las ecuaciones que describen los sistemas no lineales son complicadas, a menudo es difícil encontrar soluciones exactas. Los científicos a veces usan "aproximaciones lineales" para simplificar el problema, pero esto puede ocultar los comportamientos más interesantes y complejos del sistema.
El ejemplo del clima
El clima es un excelente ejemplo de un sistema no lineal. Un pequeño cambio en la temperatura del océano en un lugar puede tener efectos enormes y complejos en el clima de todo el mundo semanas después. Esta es una de las razones por las que es tan difícil predecir el clima con mucha antelación.
Ecuaciones No Lineales: Un Reto Matemático
En física y matemáticas, la mayoría de los problemas reales son no lineales. Las ecuaciones no lineales son un gran desafío para los científicos.
Una ecuación lineal se puede describir con un operador simple. Por ejemplo, algo como:
Donde L es un operador lineal y u es el valor que buscamos.
Una ecuación no lineal, en cambio, tiene una forma más general:
Aquí, F es una función más compleja que no sigue las reglas de linealidad.
Las soluciones de ecuaciones lineales son como piezas de un rompecabezas que encajan perfectamente. Puedes combinarlas para crear nuevas soluciones. Pero con las ecuaciones no lineales, las soluciones no se pueden combinar de esa manera, lo que las hace mucho más difíciles de resolver.
¿Qué son las Ecuaciones Diferenciales No Lineales?
Las ecuaciones diferenciales describen cómo cambian las cosas con el tiempo o el espacio. Si un sistema de estas ecuaciones no es lineal, se le llama "sistema de ecuaciones diferenciales no lineales". Resolverlas es muy variado y depende de cada problema.
Una de las mayores dificultades es que no puedes simplemente juntar soluciones conocidas para crear nuevas. En los problemas lineales, puedes usar varias soluciones simples para construir una solución general. Pero en los problemas no lineales, aunque a veces encuentres soluciones muy específicas, no puedes combinarlas fácilmente.
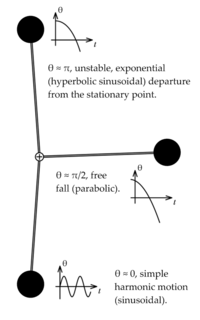
El caso del péndulo
Un ejemplo clásico de un sistema no lineal es el movimiento de un péndulo sin fricción. La ecuación que describe su movimiento es no lineal:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{d^2 \theta}{d t^2} + \sin(\theta) = 0
Aquí,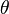 
es el ángulo del péndulo. El término 
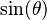(seno del ángulo) es lo que hace que la ecuación sea no lineal.
Para simplificar, los científicos a menudo usan "linealizaciones". Por ejemplo, si el péndulo se mueve solo un poquito (ángulos pequeños), 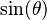es casi igual a 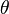. Entonces, la ecuación se vuelve lineal:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{d^2 \theta}{d t^2} + \theta = 0
Esta ecuación describe un movimiento armónico simple, como el de un resorte, que es mucho más fácil de entender. Sin embargo, esta simplificación solo funciona para ángulos pequeños y no muestra el comportamiento completo del péndulo.
Herramientas para entender los Sistemas No Lineales
Aunque son complejos, existen muchas herramientas para analizar los sistemas no lineales. Algunas de ellas son:
- Dinámica de sistemas: Ayuda a entender cómo cambian los sistemas con el tiempo.
- Teoría de la bifurcación: Estudia cómo el comportamiento de un sistema puede cambiar drásticamente cuando se modifican ciertos parámetros.
Ejemplos de Sistemas No Lineales en la Vida Real
Muchos fenómenos en la naturaleza y la tecnología se describen con ecuaciones no lineales. Algunos ejemplos importantes son:
- Las ecuaciones de campo de Einstein: Describen cómo funciona la gravedad en el universo, según la relatividad general.
- Las ecuaciones de Navier-Stokes: Describen el movimiento de los fluidos, como el agua o el aire. Son tan complejas que resolverlas es uno de los "problemas del milenio" en matemáticas.
- La óptica no lineal: Estudia cómo la luz se comporta de formas inesperadas en ciertos materiales.
- El sistema del tiempo atmosférico: Como ya mencionamos, el clima es un sistema no lineal.
- El balanceo de un uniciclo robot: Un robot que se mantiene en equilibrio sobre una sola rueda.
Galería de imágenes
-
Ilustración de un péndulo.
-
Linearizaciones de las ecuaciones del movimiento de un péndulo.
Véase también
En inglés: Nonlinear system Facts for Kids
- Aplicación lineal
- Ondas no lineales
