robot de la enciclopedia para niños

Período orbital para niños

Enciclopedia para niños
Archivo:Angular Parameters of Elliptical Orbit
Imagen que muestra cómo se miden la inclinación, la longitud del nodo ascendente y el argumento de la periapsis de un objeto en órbita.

El período orbital es el tiempo que tarda un objeto, como un planeta o una luna, en dar una vuelta completa alrededor de otro objeto más grande. Imagina que es el "año" de ese objeto.

Cuando hablamos de objetos que giran alrededor del Sol, hay dos tipos principales de períodos:

  • El período sideral es el tiempo real que tarda un objeto en completar una órbita alrededor del Sol. Se mide tomando como referencia una estrella lejana que parece fija en el espacio. Es como si lo vieras desde un lugar muy, muy lejano que no se mueve.
  • El período sinódico es el tiempo que tarda un objeto en volver a aparecer en el mismo lugar del cielo, visto desde la Tierra, en relación con el Sol. Este período es diferente porque la Tierra también se está moviendo alrededor del Sol. Es el tiempo que pasa entre dos momentos en que el objeto y el Sol están en la misma posición relativa para nosotros.

En general, el período orbital se refiere al tiempo que un cuerpo tarda en girar 360 grados alrededor de su cuerpo principal. Por ejemplo, la Tierra alrededor del Sol.

En astronomía, estos períodos se miden en unidades de tiempo como horas, días o años. Lo contrario del período orbital es la frecuencia orbital, que nos dice cuántas vueltas da un objeto en un tiempo determinado.

El período sideral y el sinódico son diferentes porque la Tierra también se mueve alrededor del Sol.

Otros Períodos Importantes

Además de los períodos sideral y sinódico, existen otros tipos de períodos que los científicos usan para estudiar las órbitas de los objetos en el espacio. Aquí te explicamos algunos:

Período Dracónico

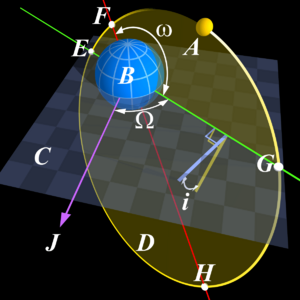
El período dracónico es el tiempo que tarda un objeto en pasar dos veces seguidas por su "nodo ascendente". El nodo ascendente es el punto donde la órbita del objeto cruza un plano de referencia (como el plano de la órbita de la Tierra alrededor del Sol) y se mueve del sur al norte. Este período es un poco diferente del sideral porque el plano de la órbita del objeto puede cambiar lentamente con el tiempo.

Período Anomalístico

El período anomalístico es el tiempo que pasa entre dos momentos en que un objeto está en su punto más cercano al cuerpo alrededor del cual orbita. Este punto se llama "periapsis" (o "perihelio" si orbita el Sol). Este período también es diferente del sideral porque la forma de la órbita del objeto puede girar lentamente.

Período Tropical

El período tropical de la Tierra es lo que conocemos como un "año". Es el tiempo que tarda la Tierra en volver a alinearse con el Sol de una manera específica, relacionada con el cambio de las estaciones. Es un poco más corto que el año sideral porque el eje de la Tierra se inclina y gira lentamente, lo que hace que se realinee con el Sol antes de completar una órbita sideral completa. Este giro lento del eje de la Tierra se llama precesión y tarda unos 25.770 años en completarse.

¿Cómo se calcula el Período Orbital?

Un cuerpo pequeño orbitando un cuerpo central

Archivo:Ellipse semi-major and minor axes
El semieje mayor (a) y el semieje menor (b) de una elipse.
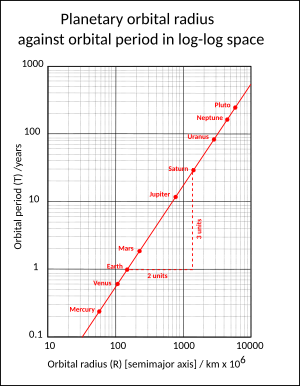
Archivo:SolarSystem Radii and Period
Gráfico que muestra la relación entre el período (T) y el semieje mayor (a) de una órbita.

Para calcular el período orbital de un objeto que gira alrededor de otro mucho más grande, usamos la tercera ley de Kepler. Esta ley nos dice que el período orbital (T) se puede calcular con la siguiente fórmula:

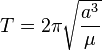
T=2\pi \sqrt{\frac{a^3}{\mu}}

Donde:

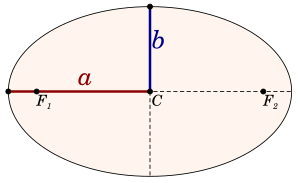
  • a es el semieje mayor de la órbita. Imagina que es la mitad del diámetro más largo de la elipse que forma la órbita.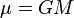
  • \mu = GM es el parámetro gravitacional estándar.

* G es la constante gravitacional, un número muy importante en física. * M es la masa del objeto más grande (el que está en el centro de la órbita).

Esta fórmula funciona para cualquier órbita cerrada, ya sea circular o elíptica.

También podemos usar esta fórmula al revés para calcular el semieje mayor de una órbita si conocemos su período orbital:

a=\sqrt[3]{\frac{\mu T^2}{4\pi^2}}=\sqrt[3]{\frac{GMT^2}{4\pi^2}}

El efecto de la densidad del cuerpo central

Si el cuerpo central es una esfera perfecta y tiene una densidad uniforme, podemos simplificar la fórmula del período orbital. Esto nos muestra que, para un objeto que orbita muy cerca de la superficie de una esfera, el período orbital depende principalmente de la densidad de esa esfera, no de su tamaño.

Por ejemplo, si un objeto pequeño orbita muy cerca de la Tierra, su período orbital sería de aproximadamente 1.41 horas. Si orbitara un cuerpo hecho de agua (como algunas lunas de Saturno), el período sería de unas 3.30 horas. Esto demuestra cómo la densidad del planeta o luna central afecta la velocidad de los objetos que lo orbitan de cerca.

Dos cuerpos orbitándose el uno al otro

Cuando dos cuerpos de tamaño similar se orbitan mutuamente (como en un sistema de estrellas binarias), la fórmula del período orbital cambia un poco. En este caso, debemos tener en cuenta las masas de ambos cuerpos:

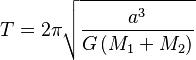
T= 2\pi\sqrt{\frac{a^3}{G \left(M_1 + M_2\right)}}

Donde:

  • a es la distancia entre los dos cuerpos (o el semieje mayor de la órbita relativa).
  • M1 + M2 es la suma de las masas de los dos cuerpos.
  • G es la constante gravitacional.

Es interesante notar que el período orbital no depende del tamaño de los cuerpos si sus densidades son las mismas.

Si la trayectoria de un objeto no es una órbita cerrada (como una parábola o una hipérbola), el movimiento no es periódico y no tiene un período orbital.

Calculando el Período Sideral y Sinódico

Imaginemos que las órbitas son círculos perfectos. La Tierra tarda aproximadamente 365.2425 días en dar una vuelta al Sol (este es su período sideral, T). Otro objeto (un planeta o la Luna) tarda un tiempo P en dar una vuelta completa al Sol (su período sideral). El tiempo que tarda en volver a aparecer en el mismo punto del cielo visto desde la Tierra es su período sinódico (S).

Podemos relacionar estos tres períodos con la siguiente fórmula:

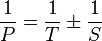
{1 \over P} = {1 \over T} \pm {1 \over S}

El signo de "más o menos" depende de si el objeto se mueve más rápido o más lento que la Tierra. Es una suma si el objeto es más rápido que la Tierra (como los planetas interiores o la Luna), y una resta si es más lento (como Marte o los planetas exteriores).

Si queremos calcular el período sinódico (S) de un planeta, conociendo el período sideral de la Tierra (T) y el del planeta (P), la fórmula es:

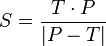
S=\dfrac{T \cdot P}{\vert P - T \vert}

Por ejemplo, los períodos sinódicos de los planetas son: Mercurio (115.88 días), Venus (583.92 días), Marte (779.94 días), Júpiter (398.88 días), Saturno (378.09 días), Urano (369.66 días) y Neptuno (367.49 días).

Y si queremos calcular el período sideral (P) de un planeta, conociendo su período sinódico (S) y el período sideral de la Tierra (T), la fórmula es:

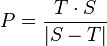
P=\dfrac{T \cdot S}{\vert S - T \vert}

Ejemplo con la Luna

Para entenderlo mejor, usemos el ejemplo de la Luna. Desde la Tierra, la Luna tarda unos 29.53 días en completar su ciclo de fases (su período sinódico, S). Sabemos que la Tierra tarda unos 365.256 días en dar una vuelta al Sol (su período sideral, T).

Usando la fórmula: 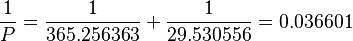{1 \over P} = {1 \over 365.256363} + {1 \over 29.530556} = 0.036601

El signo es positivo porque la Luna orbita la Tierra más rápido de lo que la Tierra orbita el Sol. Para encontrar P, hacemos 1 dividido por 0.036601, lo que nos da aproximadamente 27.321659 días.

El período sideral real de la Luna es de unos 27.321529 días, ¡así que nuestro cálculo es muy cercano!

Períodos Orbitales de los Cuerpos del Sistema Solar

Aquí tienes los períodos siderales (el tiempo que tardan en dar una vuelta completa al Sol) de algunos cuerpos de nuestro sistema solar:

Planetas

  • Mercurio: Aproximadamente 88 días
  • Venus: Aproximadamente 225 días
  • Tierra: Aproximadamente 365.256 días (1 año)
  • Marte: Aproximadamente 687 días (1 año y 321 días)
  • Júpiter: Aproximadamente 4.333 días (11 años y 315 días)
  • Saturno: Aproximadamente 10.759 días (29 años y 167 días)
  • Urano: Aproximadamente 30.685 días (84 años)
  • Neptuno: Aproximadamente 60.266 días (164 años y 280 días)

Planetas enanos y candidatos

  • Ceres: Aproximadamente 1.680 días (4.6 años)
  • Plutón: Aproximadamente 90.588 días (249 años)
  • Sedna: Aproximadamente 4.313.319 días (11.809 años)
  • Makemake: Aproximadamente 112.000 días (308 años)
  • Eris: Aproximadamente 203.450 días (557 años)

¿Cuántos Días Tiene un Año en Otros Planetas?

La siguiente tabla muestra cuánto dura un año en diferentes cuerpos celestes, pero no en días terrestres, sino en "días" de ese propio cuerpo (es decir, cuántas veces gira sobre sí mismo durante una órbita alrededor del Sol).

Es importante saber que un año terrestre tiene 366.256 rotaciones de la Tierra, no 365.256. Esto es porque un "día solar" (el tiempo que tarda el Sol en volver al mismo punto en el cielo) es un poco más largo que una rotación completa de la Tierra. La Tierra tiene que girar un poco más para que el Sol vuelva a estar en la misma dirección, ya que la Tierra también se mueve en su órbita.

Duración de la revolución de los cuerpos en número de rotaciones
Cuerpo Período de rotación

(en días terrestres)

 Período orbital

(en días terrestres)

 Período orbital

(en número de rotaciones)
Mercurio 58 65 días 87 96 días 1 499 rotaciones
Venus 243 01 días 224 69 días 0 924 rotaciones
Tierra 23 934 horas 365 256 días 365 256 rotaciones
Marte 24 630 horas 686 97 días 669 407 rotaciones
Júpiter 9 841 horas 4 332 589 días 10 566 21 rotaciones
Saturno 10 233 horas 10 759 23 días 25 234 19 rotaciones
Urano 17 9 horas 30 685 4 días 41 142 43 rotaciones
Neptuno 16 11 horas 60 216 8 días 89 708 45 rotaciones
Ceres 9 07 horas 1 680 días 4 445 42 rotaciones
Plutón 6 387 días 90 588 días 14 183 18 rotaciones
Sedna 10 273 horas 4 313 319 días 10 078 867 rotaciones
Makemake 22 83 horas 112 000 días 117 739 81 rotaciones
Eris 25 9 horas 203 450 días 188 525 09 rotaciones

Rotación Sincrónica

La rotación sincrónica ocurre cuando un cuerpo tarda el mismo tiempo en girar sobre sí mismo que en dar una vuelta completa alrededor de otro cuerpo.

El ejemplo más conocido es nuestra Luna, que siempre nos muestra la misma cara. Otro ejemplo es Caronte, la luna de Plutón. Caronte siempre le muestra la misma cara a Plutón, y Plutón también siempre le muestra la misma cara a Caronte.

Períodos Orbitales de Estrellas Binarias

Las estrellas binarias son sistemas de dos estrellas que se orbitan mutuamente. Aquí tienes algunos ejemplos de sus períodos orbitales:

Estrella binaria Período orbital
AM Canum Venaticorum 17.146 minutos
Beta Lyrae AB 12.9075 días
Alpha Centauri AB 79.91 años
Proxima Centauri – Alpha Centauri AB 500.000 años o más

Véase también

Kids robot.svg En inglés: Orbital period Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Período_orbital&oldid=4975119»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Período orbital para Niños. Enciclopedia Kiddle.