Serie de Taylor para niños
En matemática, una serie de Taylor es una forma de aproximar funciones complicadas usando una suma de polinomios más sencillos. Imagina que tienes una curva y quieres dibujarla con líneas rectas muy pequeñas. Una serie de Taylor hace algo parecido, pero con polinomios.
Estos polinomios se construyen a partir de las derivadas de la función original en un punto específico. Si ese punto es el cero (0), la serie se llama serie de Maclaurin.
Esta forma de aproximar funciones tiene varias ventajas:
- Es más fácil trabajar con los polinomios (sumarlos, restarlos, etc.) que con la función original.
- Puedes usarla para calcular valores aproximados de funciones que son difíciles de calcular directamente.
- Permite saber qué tan buena es la aproximación.
Algunas funciones no se pueden escribir como una serie de Taylor porque tienen "puntos problemáticos" (singularidades). La serie de Taylor lleva el nombre de Brook Taylor, quien la presentó en 1715.
Contenido
¿Qué es una Serie de Taylor?
Una serie de Taylor es una suma infinita de términos que se usan para representar una función. Cada término de la suma se calcula usando las derivadas de la función en un punto específico, llamado a.
La fórmula general de una serie de Taylor para una función f(x) alrededor de un punto a es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+\cdots
Donde:
- f(a) es el valor de la función en el punto a.
- f'(a), f(a), f'(a) son las derivadas de la función en el punto a.
- n! es el factorial de n (por ejemplo, 3! = 3 × 2 × 1 = 6).
- (x-a) son los términos del polinomio.
Cuando el punto a es igual a 0, la serie se llama serie de Maclaurin.
Ejemplos de Series de Maclaurin
Aquí te mostramos algunas series de Maclaurin de funciones comunes:
Función exponencial
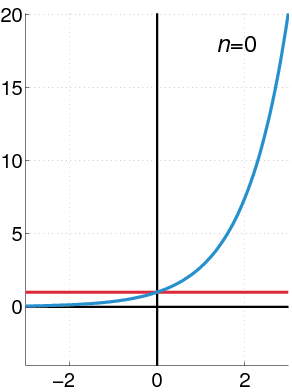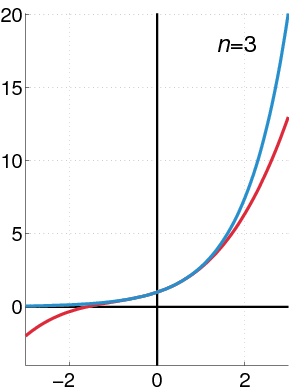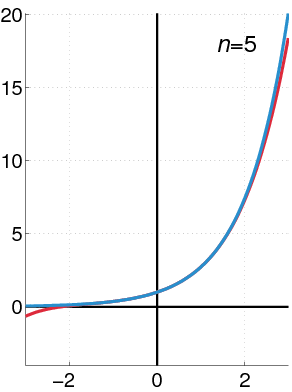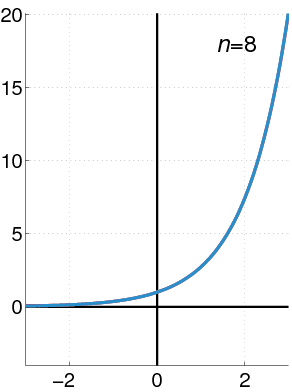
La función exponencial e^x se puede escribir como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{x} = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots Esta serie funciona para cualquier valor de x.
Logaritmo natural
El logaritmo natural de (1-x) se puede escribir como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ln(1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\cdots Esta serie funciona si el valor absoluto de x es menor que 1 (es decir, x está entre -1 y 1).
Funciones trigonométricas
Las funciones trigonométricas como el seno y el coseno también tienen sus series:
- Seno (sen x):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots Esta serie funciona para cualquier valor de x.
- Coseno (cos x):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots Esta serie también funciona para cualquier valor de x.
Historia de las Series de Taylor
La idea de sumar infinitos términos para obtener un resultado finito ha existido desde hace mucho tiempo. El filósofo Zenón de Elea ya pensaba en esto, aunque lo veía como algo imposible. Más tarde, matemáticos como Arquímedes usaron métodos similares para resolver problemas de geometría.
En el siglo XIV, un matemático hindú llamado Madhava de Sangamagrama fue uno de los primeros en usar series parecidas a las de Taylor para funciones como el seno y el coseno.
En el siglo XVII, James Gregory también trabajó en estas series. Pero fue en 1715 cuando Brook Taylor presentó una forma general para construir estas series para muchas funciones, y por eso llevan su nombre.
Las series de Maclaurin fueron nombradas así por Colin Maclaurin, un profesor de Edimburgo, quien publicó el caso especial de las series de Taylor en el siglo XVIII.
Funciones Analíticas
Una función se llama analítica si puede ser representada perfectamente por su serie de Taylor en un cierto rango de valores. Esto significa que la serie de Taylor de la función converge (se acerca cada vez más) al valor exacto de la función en ese rango.
Algunas funciones, como los polinomios, la función exponencial e^x, y las funciones seno y coseno, son analíticas en todo el plano complejo. Esto significa que sus series de Taylor siempre convergen a la función original, sin importar el valor de x.
Otras funciones, como el logaritmo o la tangente, no son analíticas en todas partes. Sus series de Taylor solo convergen en un rango limitado de valores.
Aplicaciones de las Series de Taylor
Las series de Taylor son muy útiles en matemáticas y ciencias. Algunas de sus aplicaciones incluyen:
- Aproximar funciones complejas: Permiten usar polinomios más sencillos en lugar de funciones muy complicadas para entender cómo se comportan.
- Calcular límites: Ayudan a resolver problemas de límites que de otra manera serían difíciles.
- Estimar valores: Se usan para calcular valores aproximados de números irracionales o de funciones en puntos específicos.
- Optimización: Ayudan a encontrar los puntos máximos o mínimos de una función.
- Resolver integrales: Facilitan el cálculo de algunas integrales.
Galería de imágenes
-
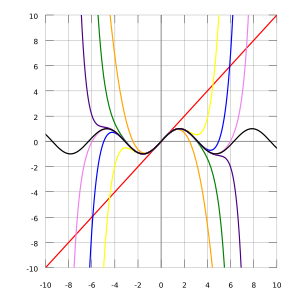
Una aproximación de octavo orden de la función coseno en el plano de los complejos
Véase también
 En inglés: Taylor series Facts for Kids
En inglés: Taylor series Facts for Kids