Astrodinámica para niños

La astrodinámica o mecánica orbital es el estudio de cómo se mueven los cohetes y las naves espaciales en el espacio. Utiliza las leyes de la física, como las leyes de movimiento y la gravedad de Isaac Newton, para calcular y predecir las trayectorias de estos objetos. Es una parte muy importante para diseñar y controlar las misiones espaciales.

Mientras que la mecánica celeste estudia el movimiento de cuerpos naturales como planetas, lunas y cometas bajo la influencia de la gravedad, la mecánica orbital se enfoca en las rutas de las naves espaciales. Esto incluye cómo cambiar su órbita, ajustar su dirección y viajar entre planetas. Los expertos en misiones espaciales usan la astrodinámica para saber qué pasará cuando una nave encienda sus motores. Aunque las leyes de Newton son muy útiles, a veces se necesita la teoría de la relatividad general para cálculos más exactos, especialmente cerca de objetos muy masivos como el Sol. La astrodinámica es la rama de la astronomía que se dedica a estudiar las órbitas, sobre todo las de los satélites artificiales y las sondas espaciales.

Astrodinámica: El Viaje de las Naves Espaciales

¿Qué es la Astrodinámica?

La astrodinámica es como la "hoja de ruta" para las naves espaciales. Nos ayuda a entender y predecir dónde estarán en el espacio y cómo podemos moverlas de un lugar a otro. Imagina que quieres enviar un mensaje a un amigo en otro continente; necesitas saber cómo se moverá el avión para llegar allí. De manera similar, la astrodinámica nos dice cómo se moverá una nave espacial para llegar a la Luna, a Marte o a cualquier otro destino.

Un Poco de Historia: ¿Quién Descubrió Esto?

Durante mucho tiempo, la mecánica orbital y la mecánica celeste eran casi lo mismo. Pero cuando empezaron los vuelos espaciales en el siglo XX, se hizo necesario diferenciarlas. Al principio, a este campo se le llamaba "dinámica espacial".

• Johannes Kepler fue el primero en describir con mucha precisión cómo se mueven los planetas alrededor del Sol, publicando sus famosas leyes en 1605.
• Isaac Newton luego explicó estas leyes de forma más general en 1687, mostrando cómo encontrar la órbita de un cuerpo a partir de solo tres observaciones. Edmund Halley usó este método para calcular las órbitas de varios cometas, incluyendo el que lleva su nombre.
• Más tarde, matemáticos como Leonhard Euler (1744) y Johann Lambert (1761-1777) mejoraron los métodos de Newton.
• Un gran avance ocurrió en 1801, cuando Carl Friedrich Gauss ayudó a "recuperar" el planeta enano Ceres. Usando solo tres observaciones, Gauss pudo determinar los seis elementos que describen completamente una órbita.
• Hoy en día, estos métodos se usan en los receptores GPS y para seguir satélites y sondas espaciales, ya que es vital saber su posición futura con mucha exactitud.
• La astrodinámica moderna fue desarrollada por el astrónomo Samuel Herrick a partir de la década de 1930. Él animó a Robert Goddard, un pionero de los cohetes, a seguir investigando las técnicas de navegación espacial. En los años 60, con la ayuda de potentes computadoras, la astrodinámica permitió que los humanos viajaran a la Luna y regresaran.

Reglas Básicas del Movimiento Orbital

Para entender cómo se mueven los satélites y las naves espaciales, podemos usar algunas reglas sencillas basadas en la física clásica. Imagina un satélite orbitando un planeta:

• Leyes de Kepler:

* Las órbitas son como elipses (óvalos), con el cuerpo más pesado (el planeta) en uno de sus puntos focales. Una órbita circular es un tipo especial de elipse. * Una línea imaginaria que une el planeta y el satélite cubre la misma área en el mismo tiempo, sin importar en qué parte de la órbita se encuentre el satélite. * El tiempo que tarda un satélite en completar una órbita (su período) está relacionado con su distancia promedio al planeta. Cuanto más lejos, más tiempo tarda.

• Si no se aplica ninguna fuerza (como encender un motor), la órbita de un satélite no cambiará.
• Un satélite en una órbita baja se mueve más rápido que uno en una órbita más alta, porque la gravedad es más fuerte cerca del planeta.
• Si un satélite enciende su motor en un solo punto de su órbita, volverá a pasar por ese mismo punto en cada órbita siguiente, aunque el resto de su trayectoria cambiará.
• Para cambiar una órbita circular a una elíptica, si el satélite empuja en dirección opuesta a su movimiento, bajará y alcanzará su punto más bajo (periapsis) a 180 grados del punto de encendido. Si empuja en la dirección de su movimiento, subirá y alcanzará su punto más alto (apoapsis) a 180 grados del punto de encendido.

A veces, estas reglas pueden parecer extrañas. Por ejemplo, si dos naves espaciales están en la misma órbita circular y quieren unirse, la nave de atrás no puede simplemente acelerar. Si lo hiciera, su órbita cambiaría, subiría y, de hecho, se ralentizaría con respecto a la nave de adelante. Por eso, unirse en el espacio requiere cálculos muy precisos y a menudo varios encendidos de motores durante horas o días.

Además, en la realidad, hay otros factores que afectan las órbitas, como la resistencia del aire en órbitas bajas.

Velocidad de Escape

La velocidad de escape es la velocidad mínima que un objeto necesita para "escapar" de la gravedad de un cuerpo celeste y no volver a caer. Imagina lanzar una pelota hacia arriba: si la lanzas muy fuerte, podría salir de la Tierra.

La energía total de un objeto en el espacio es la suma de su energía de movimiento (cinética) y su energía de posición (potencial). Para escapar, la energía total debe ser cero o positiva. Esto significa que la velocidad debe ser al menos:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ v = \sqrt{\frac{2 G M}{r}} \,

Donde:

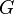• es la constante de la gravedad.
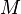• es la masa del planeta o cuerpo del que se quiere escapar.
• es la distancia desde el centro del cuerpo.

Desde la superficie de la Tierra, la velocidad de escape es de unos 11 kilómetros por segundo. Pero para escapar del sistema solar desde la Tierra, se necesita una velocidad de unos 42 kilómetros por segundo, aunque la velocidad de la Tierra en su órbita ayuda un poco.

Fórmulas para Órbitas Libres

Las órbitas son formas geométricas llamadas secciones cónicas (círculos, elipses, parábolas o hipérbolas). La distancia de un cuerpo en órbita se puede describir con una fórmula:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r = \frac{ p }{1 + e \cos \theta}

Donde:

• es la distancia.
• es la excentricidad (qué tan "estirada" es la elipse).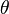
• es el ángulo del cuerpo en su órbita.
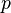• es un parámetro de la órbita.

Órbitas Circulares

Una órbita circular es un caso especial de elipse donde la excentricidad es cero. La velocidad de un cuerpo en una órbita circular a una distancia de un cuerpo de masa 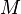se calcula así:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \ v = \sqrt{\frac{GM} {r}\ }

Donde 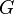es la constante de gravitación universal.

Órbitas Elípticas

Si la excentricidad está entre 0 y 1, la órbita es elíptica. En estas órbitas, el cuerpo tiene un punto más cercano al centro (periapsis) y un punto más lejano (apoapsis).

El tiempo que tarda un cuerpo en completar una órbita elíptica (su período orbital) se calcula con:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T=2\pi\sqrt{a^3\over{\mu}}

Donde:

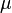• es el parámetro gravitacional estándar.
• es la longitud del semieje mayor (la mitad del eje más largo de la elipse).

La velocidad de un cuerpo en una órbita elíptica se calcula con la ecuación de Vis-viva:

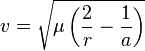
Órbitas Parabólicas

Si la excentricidad es exactamente 1, la órbita es parabólica. Esto significa que el objeto tiene la velocidad justa para escapar de la gravedad, pero no más. Su energía orbital es cero.

La velocidad en cualquier punto de una trayectoria parabólica es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v=\sqrt{2\mu\over{r}}

Órbitas Hiperbólicas

Si la excentricidad es mayor que 1, la órbita es hiperbólica. Esto significa que el objeto tiene más que la velocidad de escape y se alejará para siempre del cuerpo central. Su energía orbital es positiva.

La velocidad de un cuerpo en una trayectoria hiperbólica cuando está muy lejos del cuerpo central se llama "exceso de velocidad hiperbólica" ():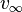

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): v_\infty=\sqrt{\mu\over{-a}}\,\!

Cálculo de Trayectorias

Para calcular las trayectorias de las naves espaciales, se usan diferentes métodos:

• Ecuación de Kepler: Es una forma clásica de calcular la posición de un cuerpo en una órbita elíptica en un momento dado. Es un poco complicada de resolver directamente, por lo que a menudo se usan métodos numéricos (con computadoras) para encontrar la solución.
• Aproximación Cónica Parcheada: Para viajes interplanetarios, esta técnica simplifica el problema. Se divide el viaje en fases, y en cada fase se considera solo la gravedad del cuerpo celeste más cercano. Por ejemplo, al ir de la Tierra a Marte, primero se considera la gravedad de la Tierra, luego la del Sol, y finalmente la de Marte. Esta aproximación es útil para estimar el combustible necesario, pero no es lo suficientemente precisa para guiar una nave espacial.
• Formulación de Variable Universal: Este método es más moderno y funciona bien para todo tipo de órbitas (circulares, elípticas, parabólicas e hiperbólicas). Es muy útil para cálculos precisos y cuando se consideran pequeñas fuerzas adicionales que afectan la órbita.

Perturbaciones: Cuando las Órbitas Cambian

En la realidad, las órbitas no son perfectas elipses o círculos. Hay otras fuerzas, llamadas perturbaciones, que hacen que las órbitas cambien con el tiempo. Algunas de estas fuerzas son:

• Las protuberancias de la Tierra (no es una esfera perfecta) causan pequeños cambios en la órbita de los satélites.
• La gravedad de la Luna y el Sol también afecta las órbitas de los satélites terrestres.
• El arrastre de la atmósfera (incluso muy tenue) frena a los satélites en órbitas bajas, haciendo que pierdan altura.

Aunque estas perturbaciones son pequeñas, con el tiempo pueden acumularse y hacer que el comportamiento de una órbita sea impredecible (caótico). Sin embargo, los ingenieros espaciales pueden usar estas perturbaciones a su favor para mantener las naves en su lugar o para ajustar sus trayectorias.

Leyes Fundamentales de la Astrodinámica

Las leyes principales de la astrodinámica son la ley de la gravitación universal de Newton y las leyes de movimiento de Newton. La herramienta matemática clave para estudiarlas es el cálculo.

Una característica interesante es que, en principio, cada órbita y trayectoria fuera de las atmósferas es reversible. Esto significa que si pudieras "rebobinar" el tiempo, la nave espacial seguiría la misma trayectoria en sentido contrario.

Para simplificar los cálculos, a menudo se hacen algunas suposiciones: que no hay interferencia de otros cuerpos, que la masa de un cuerpo es mucho mayor que la del otro, y que otras fuerzas (como el viento solar o el arrastre atmosférico) son insignificantes. Aunque se pueden hacer cálculos más precisos sin estas suposiciones, a menudo la diferencia no es lo suficientemente grande como para justificar la complejidad adicional.

Las leyes de Kepler del movimiento planetario se pueden obtener de las leyes de Newton si solo se considera la fuerza de gravedad del cuerpo central. Si un cohete enciende sus motores, las leyes de Newton siguen siendo válidas, pero las leyes de Kepler ya no describen la órbita hasta que el motor se apaga y se establece una nueva órbita. Las tres leyes de Kepler son:

1. La órbita de cada planeta es una elipse con el Sol en uno de sus focos.
2. Una línea que une un planeta y el Sol barre áreas iguales en tiempos iguales.
3. Los cuadrados de los períodos orbitales de los planetas son proporcionales a los cubos del semieje mayor de sus órbitas.

Maniobras Orbitales

En el vuelo espacial, una maniobra orbital es cuando se usan los motores de una nave espacial para cambiar su órbita. Si la nave está lejos de la Tierra (por ejemplo, orbitando el Sol), se le llama maniobra en el espacio profundo.

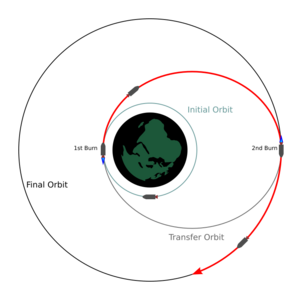
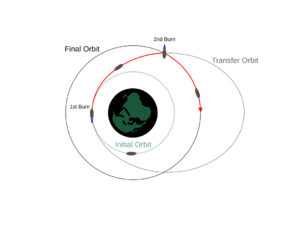
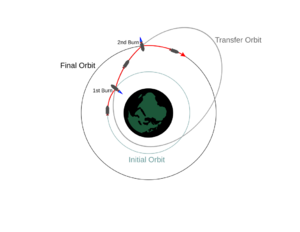
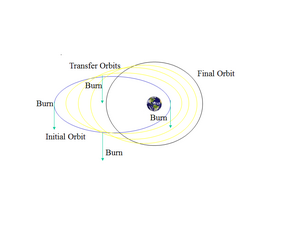
Transferencia Orbital

Las órbitas de transferencia son rutas elípticas que permiten a las naves espaciales moverse de una órbita a otra. Generalmente, necesitan un impulso al principio, otro al final, y a veces más impulsos intermedios.

• Transferencia de Hohmann: Es la forma más eficiente de cambiar de una órbita circular a otra, usando la menor cantidad de combustible.
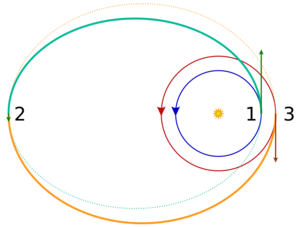
• Transferencia Bielíptica: A veces puede requerir menos energía que la de Hohmann, pero tarda más tiempo.
• Transferencias más rápidas: Se pueden usar otras órbitas que crucen las órbitas de origen y destino, pero esto gasta más combustible.
• Si las órbitas no están en el mismo plano, el cambio de plano debe hacerse en el punto donde los planos se cruzan.

Una transferencia de Hohmann de una órbita circular baja a una órbita circular más alta.

Una transferencia bi-elíptica de una órbita de partida circular baja (azul oscuro), a una órbita circular más alta (roja).

Transferencia genérica de dos impulsos elípticos entre dos órbitas circulares.

Una transferencia general desde una órbita circular baja a una órbita circular superior.

Una secuencia óptima para transferir un satélite de una órbita supersincrónica a una órbita geosincrónica usando la propulsión eléctrica.

Asistencia Gravitatoria y Efecto Oberth

• Asistencia Gravitatoria: Una nave espacial puede pasar cerca de un planeta y usar su gravedad para cambiar de dirección y velocidad. Esto es como un "tirachinas" cósmico que ayuda a acelerar o frenar la nave sin gastar mucho combustible. El planeta pierde una cantidad mínima de energía, pero debido a su enorme masa, el efecto en su órbita es insignificante.
• Efecto Oberth: Este efecto dice que los motores de propulsión funcionan mejor cuando la nave se mueve a alta velocidad. Por eso, es más eficiente encender los motores cuando la nave está cerca de un cuerpo gravitatorio, donde su velocidad es mayor. Esto puede multiplicar la efectividad del combustible.

Red de Transporte Interplanetario y Órbitas Difusas

Hoy en día, las computadoras pueden encontrar rutas muy complejas usando las interacciones gravitatorias de los planetas y lunas del sistema solar. Estas rutas, llamadas Red de Transporte Interplanetario, pueden ser muy eficientes en cuanto a combustible, pero a menudo tardan muchos años en completarse. Un ejemplo es la misión Génesis, que visitó un punto especial entre la Tierra y el Sol y regresó usando muy poco propulsor.

Galería de imágenes

• 

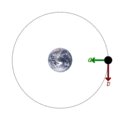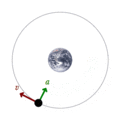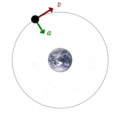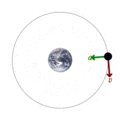
  Un satélite en órbita alrededor de la Tierra tiene una velocidad tangencial y una aceleración hacia dentro.

Véase también

En inglés: Astrodynamics Facts for Kids