Regla y compás para niños
La construcción con regla y compás es una forma especial de dibujar figuras geométricas. Para hacer estas construcciones, solo puedes usar dos herramientas: una regla y un compás que son "ideales". Esto significa que no son como los que usamos en la escuela, sino versiones perfectas y con reglas muy estrictas.
Los antiguos griegos fueron los primeros en establecer estas reglas. Querían saber qué figuras se podían dibujar usando solo estos dos instrumentos.
La regla ideal es muy larga, no tiene marcas para medir distancias y solo tiene un borde. El compás ideal se cierra solo cuando lo levantas del papel, así que no puede "recordar" la distancia que tenías entre sus puntas. Aunque esto parece difícil, los matemáticos encontraron formas de mover distancias de manera indirecta.
Curiosamente, cualquier figura que puedas dibujar con regla y compás, también puedes dibujarla usando solo el compás.
Algunos de los problemas más famosos que los griegos intentaron resolver con regla y compás son:
- La cuadratura del círculo: dibujar un cuadrado con la misma área que un círculo dado.
- La duplicación del cubo: dibujar el lado de un cubo que tenga el doble de volumen que otro cubo dado.
- La trisección del ángulo: dividir un ángulo en tres partes iguales.
- La construcción del heptágono regular: dibujar un polígono de siete lados iguales.
¡Lo interesante es que se demostró que estos problemas son imposibles de resolver usando solo la regla y el compás ideales! A pesar de esto, muchas personas siguen intentándolo.
Contenido
- La regla y el compás ideales
- Los tres problemas clásicos imposibles
- Historia de las construcciones
- Las construcciones básicas
- Construcciones clásicas con regla y compás
- Puntos y longitudes que se pueden construir
- Ángulos que se pueden construir
- Construcción de polígonos regulares
- Construcciones de figuras inscritas
- Construcciones con otras herramientas
- Investigaciones recientes
- Galería de imágenes
- Véase también
La regla y el compás ideales

La regla y el compás que se usan en estas construcciones son ideas matemáticas, no herramientas físicas. Son como los números o las formas geométricas que estudias en matemáticas.
- El compás puede dibujar círculos de cualquier tamaño. Pero, a diferencia de los compases reales, no tiene marcas para fijar una abertura. Solo puedes abrirlo entre dos puntos que ya hayas dibujado. Además, este compás "ideal" se cierra en cuanto lo levantas del papel, olvidando el tamaño del círculo que acaba de trazar.
- La regla no tiene marcas para medir y solo tiene un borde. Su única función es dibujar una línea recta que pase por dos puntos que ya existen en el papel, o alargar una línea ya dibujada tanto como quieras.
Las construcciones con regla y compás se hacen en la mente, con una precisión perfecta, como si fueran cálculos de álgebra. No son dibujos con imperfecciones como los que hacemos en un papel.
Durante más de dos mil años, los matemáticos se preguntaron qué se podía y qué no se podía hacer con estas herramientas. El verdadero interés científico surgió al descubrir los límites de lo que era posible.
Los tres problemas clásicos imposibles
Estos tres problemas clásicos de la geometría resistieron miles de intentos de solución con regla y compás. A mediados del siglo XIX, se demostró matemáticamente que son imposibles de resolver con estas herramientas.
- Cuadratura del círculo: El objetivo es dibujar un cuadrado que tenga exactamente la misma superficie que un círculo que ya está dibujado. Se ha demostrado que esto es imposible porque requiere encontrar un tipo de número especial llamado "número trascendente" (como el número pi,
 ), y con regla y compás solo se pueden construir números "algebraicos". Por eso, la frase "cuadrar el círculo" se usa para decir que algo es imposible.
), y con regla y compás solo se pueden construir números "algebraicos". Por eso, la frase "cuadrar el círculo" se usa para decir que algo es imposible.
- Duplicación del cubo: Aquí se pide dibujar el lado de un cubo que tenga el doble de volumen que otro cubo dado. Esto es imposible porque para resolverlo necesitarías construir la raíz cúbica de 2 (
![\sqrt[3]{2}](/images/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) ). Aunque este es un número algebraico, no se puede obtener solo con las operaciones que permite la regla y el compás (sumas, restas, multiplicaciones, divisiones y raíces cuadradas).
). Aunque este es un número algebraico, no se puede obtener solo con las operaciones que permite la regla y el compás (sumas, restas, multiplicaciones, divisiones y raíces cuadradas).
- Trisección del ángulo: Consiste en dividir un ángulo dado en tres ángulos más pequeños, todos del mismo tamaño. Se ha demostrado que esto es imposible en general. Por ejemplo, si intentaras trisecar un ángulo de 60 grados, necesitarías construir un ángulo de 20 grados. Pero el coseno de 20 grados es un número que no se puede construir con regla y compás.
Estos problemas sí se pueden resolver si se usan otras herramientas o métodos que van más allá de la regla y el compás ideales.
Historia de las construcciones
Los matemáticos griegos fueron los primeros en explorar las construcciones con regla y compás. Descubrieron cómo sumar, restar, multiplicar, dividir y sacar raíces cuadradas de longitudes. También sabían cómo dividir ángulos por la mitad, duplicar cuadrados (hacer un cuadrado con el doble de área) y construir polígonos regulares de 3, 4 y 5 lados, o uno con el doble de lados que otro ya dado.
Sin embargo, no pudieron trisecar ángulos (excepto en casos especiales como el ángulo recto) ni cuadrar el círculo o duplicar el cubo.
Con el tiempo, otros matemáticos como Hipócrates y Menecmo mostraron que la duplicación del cubo era posible usando curvas especiales que no se podían dibujar con regla y compás. Hipias y Nicomedes también usaron curvas para resolver la trisección del ángulo y la cuadratura del círculo.
Pasaron dos mil años sin que se resolviera el misterio de estos problemas, hasta que en 1796, Gauss demostró que un polígono regular de 17 lados sí podía construirse con estas herramientas. En 1837, Pierre Wantzel probó la imposibilidad de la trisección del ángulo y la duplicación del cubo. Finalmente, en 1882, Lindemann demostró que el número  es trascendente, lo que confirmó la imposibilidad de la cuadratura del círculo.
es trascendente, lo que confirmó la imposibilidad de la cuadratura del círculo.
Las construcciones básicas
Todas las construcciones que se hacen con regla y compás se basan en cinco pasos muy simples. En cada paso, usas los puntos, líneas y círculos que ya has creado.
Las cinco construcciones básicas son:
- Dibujar la línea recta que une dos puntos que ya existen.
- Dibujar un círculo con centro en un punto dado y que pase por otro punto dado.
- Encontrar el punto donde se cruzan dos líneas rectas que no son paralelas.
- Encontrar el punto o los puntos donde se cruzan una línea y un círculo (si se cruzan).
- Encontrar el punto o los puntos donde se cruzan dos círculos (si se cruzan).
Por ejemplo, si tienes dos puntos, puedes dibujar una línea recta que los una. O puedes dibujar dos círculos, usando cada punto como centro. Si estos círculos se cruzan, obtendrás dos puntos nuevos. Si unes los puntos originales con uno de los puntos nuevos, ¡habrás construido un triángulo equilátero! Así, construir un triángulo equilátero a partir de uno de sus lados es muy fácil con regla y compás.
Construcciones clásicas con regla y compás
Las construcciones más comunes que se pueden hacer con regla y compás incluyen:
- Construir la mediatriz de un segmento (la línea que lo divide en dos partes iguales y es perpendicular a él).
- Encontrar el punto medio de un segmento.
- Dibujar una línea perpendicular a otra que pase por un punto dado.
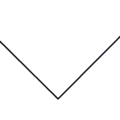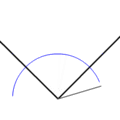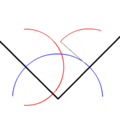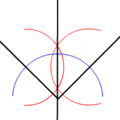
- Dividir un ángulo por la mitad (bisecar un ángulo).
- Reflejar un punto respecto a una línea.
- Construir la línea tangente a un círculo que pasa por un punto dado.
- Construir la circunferencia que pasa por tres puntos que no están en la misma línea.
- Construir la línea paralela a otra que pase por un punto dado.
Puntos y longitudes que se pueden construir
Para entender por qué algunos problemas son imposibles, los matemáticos estudian qué tipos de números se pueden "construir" con regla y compás.
Imagina que tienes dos puntos. Puedes llamar a uno "0" y al otro "1". Así, puedes crear un sistema de coordenadas como el que usas en matemáticas. Con la regla y el compás, puedes dibujar el eje X y el eje Y, y definir una unidad de medida.
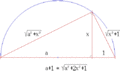
Los puntos que puedes construir con regla y compás son aquellos cuyas coordenadas se pueden expresar usando números racionales (como fracciones) y raíces cuadradas de esos números, o de combinaciones de ellos. Por ejemplo, puedes construir 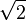 o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{3+\sqrt{5}} .
o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{3+\sqrt{5}} .
Esto significa que cualquier número que se pueda construir con regla y compás es un "número algebraico" (es decir, es la solución de una ecuación polinómica con coeficientes enteros), y el grado de esa ecuación debe ser una potencia de 2 (como 2, 4, 8, etc.).
La clave para demostrar que algo es imposible es mostrar que para resolver el problema, necesitarías construir un número que no se puede expresar de esta manera. Por ejemplo, para duplicar el cubo, necesitas ![\sqrt[3]{2}](/images/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) , que no se puede obtener solo con raíces cuadradas.
, que no se puede obtener solo con raíces cuadradas.
Ángulos que se pueden construir
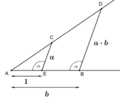
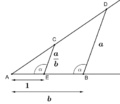
Los ángulos que se pueden construir con regla y compás son aquellos cuyo coseno (o seno o tangente) es un número que se puede construir.
Por ejemplo, el polígono regular de 17 lados (llamado heptadecágono) se puede construir. Esto se debe a que el coseno del ángulo central de un heptadecágono es un número muy complejo que, sin embargo, se puede expresar usando solo raíces cuadradas. ¡Esto fue descubierto por Gauss!
Si el coseno de un ángulo es construible, puedes dibujar un segmento con esa longitud en el eje X. Luego, con el compás, puedes encontrar el punto en un círculo unitario que corresponde a ese coseno, y así construir el ángulo deseado.
Construcción de polígonos regulares
Algunos polígonos regulares, como el hexágono (6 lados) y el pentágono (5 lados), son fáciles de construir con regla y compás. Otros, como el heptágono (7 lados), no lo son.
Gauss descubrió en 1801 que un polígono regular de n lados se puede construir con regla y compás si los números primos impares que dividen a n son "primos de Fermat" distintos. Los primos de Fermat son números primos muy especiales.
Algunos de los primeros polígonos regulares que se pueden construir son los de: 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272...
Se sabe que hay infinitos polígonos construibles con un número par de lados. Sin embargo, solo se conocen 31 polígonos regulares construibles con un número impar de lados.
Construcciones de figuras inscritas
Es común en geometría buscar cómo dibujar una figura dentro de otra, por ejemplo, un círculo dentro de un triángulo, o al revés. Para esto, se usan pasos como dividir los ángulos de un triángulo por la mitad para encontrar su centro.
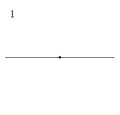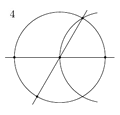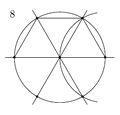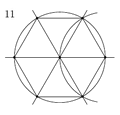
Un ejemplo más complejo es construir un círculo dentro de un segmento circular (una parte de un círculo cortada por una línea recta). Para esto, se toman en cuenta las condiciones de tangencia (que las figuras se toquen en un solo punto).
Construcciones con otras herramientas
Aunque la regla y el compás tienen límites, otras herramientas o métodos pueden resolver los problemas "imposibles":
- Solo con compás: El teorema de Mohr-Mascheroni dice que cualquier construcción que se pueda hacer con regla y compás (excepto dibujar una línea recta) también se puede hacer solo con compás.
- Reglas marcables: Algunos matemáticos antiguos usaban reglas con marcas para medir distancias. Con estas reglas, se podían resolver problemas como la trisección del ángulo y la duplicación del cubo. Sin embargo, la cuadratura del círculo seguía siendo imposible.
- Origami: La papiroflexia, o el arte de doblar papel, es sorprendentemente poderosa. Las reglas del origami permiten resolver ecuaciones cúbicas, lo que significa que también puede resolver la duplicación del cubo y la trisección del ángulo. Pero, al igual que con las reglas marcables, el origami no puede cuadrar el círculo.
- Trisectar un segmento de recta: Es posible dividir un segmento de recta en tres partes iguales (o en cualquier número de partes) usando el Teorema de Tales.
Para ello, se dibuja otro segmento desde uno de los extremos del primero. Luego, se marcan puntos equidistantes en el nuevo segmento. Al unir el último punto con el extremo opuesto del segmento original y trazar líneas paralelas, el segmento original quedará dividido en partes iguales.
Investigaciones recientes
Simon Plouffe ha investigado cómo la regla y el compás pueden usarse como una especie de "computadora" simple, mostrando su sorprendente capacidad de cálculo.
Galería de imágenes
-
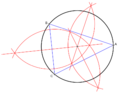
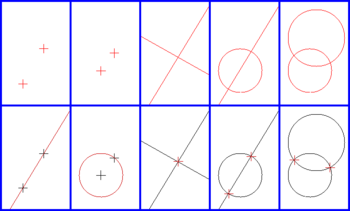
Recta tangente a un círculo con centro en
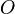 que pasa por
que pasa por  . Se construye una circunferencia de diámetro
. Se construye una circunferencia de diámetro 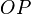 . Las rectas que determinadas por
. Las rectas que determinadas por  y las intersecciones
y las intersecciones 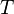 son tangentes al círculo inicial (ver en enlace en la lista anterior)
son tangentes al círculo inicial (ver en enlace en la lista anterior)
Véase también
 En inglés: Compass and straightedge construction Facts for Kids
En inglés: Compass and straightedge construction Facts for Kids
- Historia de la geometría
- Inversión en el plano
- Las matemáticas del origami
- Número trascendente
- Politopo regular (construcción de polígonos y poliedros)
- El problema de Apolonio
- Proporción áurea







 y su punto medio
y su punto medio 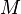 .
.
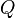 es la reflexión de
es la reflexión de