Rectángulo para niños
Datos para niños Rectángulo |
||
|---|---|---|
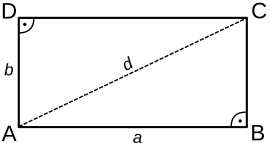
Rectángulo, con sus lados paralelos e iguales dos a dos y sus cuatro ángulos rectos
|
||
| Características | ||
| Tipo | Cuadrilátero, paralelogramo, hiperrectángulo | |
| Lados | 4 | |
| Vértices | 4 | |
| Grupo de simetría | Diedral (D2), [2], (*22), orden 4 | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Rombo | |
| Propiedades | ||
| Convexo, isogonal, cíclico Ángulos opuestos y lados cogruentes. |
||
En geometría plana, un rectángulo es una figura con cuatro lados. Todos sus ángulos son rectos, es decir, miden 90 grados. Los lados opuestos de un rectángulo siempre tienen la misma longitud y son paralelos entre sí. Si un rectángulo tiene sus cuatro lados iguales, entonces es un cuadrado.
La palabra "rectángulo" viene del latín rectangulus. Esta palabra se forma de rectus, que significa "recto" o "correcto", y angulus, que significa "ángulo". Así, un rectángulo es una figura con "ángulos rectos".
Los rectángulos son muy comunes en nuestra vida diaria. Los vemos en puertas, ventanas, libros y pantallas de televisión. También son importantes en problemas de teselado, que es cuando cubrimos una superficie con figuras sin dejar huecos.
Contenido
¿Qué es un Rectángulo?
Un rectángulo es un tipo especial de cuadrilátero, que es cualquier figura geométrica con cuatro lados. Se define por tener cuatro ángulos rectos (de 90°). También es un paralelogramo, lo que significa que sus lados opuestos son paralelos.
¿Cómo se define un Rectángulo?
Un rectángulo se puede entender como un paralelogramo que tiene al menos un ángulo recto. Como es un paralelogramo, si tiene un ángulo recto, automáticamente los otros tres también serán rectos. Esto se debe a que los ángulos opuestos en un paralelogramo son iguales, y los ángulos consecutivos suman 180°.
¿Cómo se calcula el Perímetro y el Área?
Para entender mejor un rectángulo, podemos calcular su perímetro y su área.
Perímetro de un Rectángulo
El perímetro es la medida del contorno de una figura. Para un rectángulo, se suman las longitudes de sus cuatro lados. Si llamamos 'a' a la longitud de un lado y 'b' a la longitud del otro lado (los lados adyacentes), la fórmula es:
- P = 2 × a + 2 × b
- O también: P = 2 × (a + b)
Área de un Rectángulo
El área es la medida de la superficie que cubre una figura. Para un rectángulo, se multiplica la longitud de un lado por la longitud del lado adyacente. Usando las mismas letras 'a' y 'b':
- A = a × b
Propiedades Importantes de los Rectángulos
Los rectángulos tienen varias propiedades interesantes que los hacen únicos:
- Sus lados opuestos no solo son paralelos, sino que también tienen la misma longitud.
- Las dos diagonales de un rectángulo (líneas que conectan vértices opuestos) siempre tienen la misma longitud.
- Las diagonales se cruzan justo en el centro del rectángulo. Este punto es el centro de simetría de la figura.
- Un rectángulo tiene dos ejes de simetría. Estos ejes son líneas imaginarias que dividen el rectángulo en dos partes iguales y pasan por el centro, siendo paralelas a sus lados.
- Cualquier rectángulo puede dibujarse dentro de una circunferencia. Las diagonales del rectángulo son los diámetros de esa circunferencia.
- Si unes los puntos medios de los lados de un rectángulo, la figura que se forma en el centro es un rombo.
Simetría de un Rectángulo
Los rectángulos tienen dos tipos de simetría:
- Simetría axial: Hay dos líneas (ejes) que dividen el rectángulo en dos mitades idénticas. Estas líneas son perpendiculares entre sí y pasan por el centro del rectángulo.
- Simetría central: El punto donde se cruzan las diagonales es el centro de simetría. Si giras el rectángulo 180 grados alrededor de este punto, se verá exactamente igual.
Clasificación de los Rectángulos
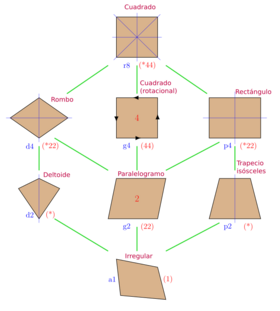
Un rectángulo es parte de una familia de figuras geométricas:
- Un rectángulo es un tipo especial de paralelogramo donde todos sus ángulos son rectos.
- Un paralelogramo es un tipo especial de trapecio donde ambos pares de lados opuestos son paralelos.
- Un trapecio es un cuadrilátero convexo que tiene al menos un par de lados opuestos paralelos.
- Un cuadrilátero es cualquier figura con cuatro lados.
Tipos Especiales de Rectángulos
Existen algunos rectángulos famosos por sus proporciones:
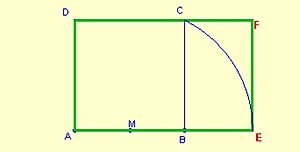
- El rectángulo áureo: También conocido como rectángulo de oro o rectángulo Φ (Phi). La relación entre su lado más largo y su lado más corto es un número especial llamado razón áurea (aproximadamente 1.618). Se considera que tiene proporciones muy agradables a la vista y se ha usado mucho en arte y arquitectura.
- El rectángulo raíz de 2: Este rectángulo tiene una relación entre sus lados igual a la raíz cuadrada de dos (aproximadamente 1.414). Lo interesante de este rectángulo es que si lo divides por la mitad a lo largo de su lado más largo, obtienes dos rectángulos más pequeños que tienen exactamente la misma proporción que el original. Por eso, se usa para los tamaños de papel estándar, como los de las normas ISO 216 (por ejemplo, el tamaño A4).
- Doble cuadrado: Es un rectángulo donde un lado es el doble de largo que el otro (relación 2:1).
- Pantallas de televisión: Las pantallas de televisión y monitores son rectángulos. Antes, la mayoría tenían una proporción de 4:3 (cuatro unidades de ancho por tres de alto). Hoy en día, las pantallas de alta definición suelen tener una proporción de 16:9.
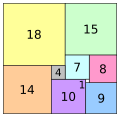
Teselados con Rectángulos
Los rectángulos son muy útiles para crear teselados, que son patrones que cubren una superficie sin dejar huecos ni superponerse. Aquí tienes algunos ejemplos de cómo se usan los rectángulos en mosaicos:
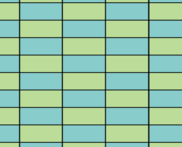 Unión apilada. |
 Unión desplazada. |
 Trenzado de cesta. |
 Trenzado de cesta. |
 Espina de pez. |
Galería de imágenes
Véase también
 En inglés: Rectangle Facts for Kids
En inglés: Rectangle Facts for Kids
- Anexo:Ecuaciones de figuras geométricas
- Cuadrilátero
- Paralelogramo
- Cuadrado