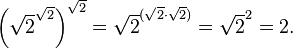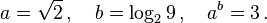Prueba constructiva para niños
En matemáticas, una prueba constructiva es una forma de demostrar que algo existe, pero no solo diciendo que existe, sino también mostrando cómo construirlo o cómo encontrarlo. Imagina que quieres demostrar que existe un tesoro: una prueba constructiva te daría un mapa exacto para llegar a él.
Esto es diferente de una prueba no constructiva (también llamada prueba de existencia), que solo te dice que el tesoro existe, pero sin darte ninguna pista de dónde está o cómo encontrarlo. Es como si alguien te dijera "hay un tesoro", pero no te da un mapa.
A veces, una prueba constructiva también se refiere a un tipo de prueba que sigue las reglas de la matemática constructiva. Esta forma de pensar en las matemáticas es un poco especial porque solo acepta cosas que se pueden "construir" o encontrar de forma clara. Por ejemplo, no usan la idea de que algo "es o no es" sin una forma de saber cuál de las dos opciones es la correcta.
Algunas pruebas no constructivas funcionan mostrando que si algo fuera falso, entonces habría un problema o una contradicción. Por lo tanto, la afirmación original debe ser verdadera.
Las pruebas constructivas son importantes porque nos ayudan a crear algoritmos, que son como recetas paso a paso para resolver problemas.
Contenido
¿Cómo surgieron estas ideas?
Hasta finales del siglo XIX, casi todas las demostraciones en matemáticas eran constructivas. Esto significa que los matemáticos siempre mostraban cómo encontrar o construir lo que estaban demostrando.
Las primeras pruebas que no eran constructivas aparecieron con las ideas de Georg Cantor sobre los conjuntos infinitos y la forma en que se definen los números reales.
Uno de los primeros ejemplos importantes de una prueba no constructiva fue el teorema de los ceros de Hilbert. Este teorema decía que existían ciertos objetos matemáticos sin mostrar cómo encontrarlos. Esto sorprendió mucho a los matemáticos de la época. Uno de ellos, Paul Gordan, incluso dijo: "esto no es matemática, es teología".
Veinticinco años después, una matemática llamada Grete Hermann encontró una forma de calcular esos objetos, lo que dio un método para encontrarlos, aunque su prueba se basó en el resultado de Hilbert.
Ejemplos de pruebas
Pruebas no constructivas: ¿Existe sin mostrar cómo?
Pensemos en el teorema que dice que hay una cantidad infinita de números primos. La demostración original de Euclides es constructiva, porque te da una forma de encontrar un nuevo número primo.
Pero hay una forma más sencilla de explicarlo que es no constructiva: Imagina que solo hay una cantidad limitada de números primos, y que el más grande es n. Ahora, piensa en el número que se obtiene al multiplicar todos esos primos y sumarle 1 (n! + 1). Este nuevo número o es primo, o sus factores primos son más grandes que n. Esto demuestra que siempre hay un primo más grande que n, lo cual contradice la idea de que n era el primo más grande. Esta prueba no te dice cuál es ese nuevo primo, solo que existe.
Ahora, veamos otro ejemplo: "existen números irracionales  y
y  tales que
tales que 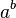 es un número racional". Este teorema se puede probar de forma no constructiva.
es un número racional". Este teorema se puede probar de forma no constructiva.
Una prueba de 1953 de Dov Jarden es un buen ejemplo:
CURIOSA
Dov Jarden Jerusalén
339. Una prueba simple de que una potencia de un número irracional elevado a un exponente irracional puede ser racional.
es racional o irracional. Si es racional, nuestro enunciado está probado. Si es irracional,
prueba nuestra afirmación.
Explicado con más detalle:
- Sabemos que
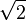 es un número irracional (no se puede escribir como una fracción simple), y que 2 es racional (se puede escribir como 2/1).
es un número irracional (no se puede escribir como una fracción simple), y que 2 es racional (se puede escribir como 2/1). - Consideremos el número
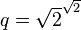 . Este número puede ser racional o irracional.
. Este número puede ser racional o irracional. - Si
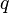 es racional, entonces ya encontramos nuestro ejemplo:
es racional, entonces ya encontramos nuestro ejemplo:  y
y  serían ambos
serían ambos 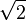 .
. - Si
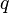 es irracional, entonces el teorema también es verdadero. En este caso,
es irracional, entonces el teorema también es verdadero. En este caso,  sería
sería 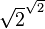 y
y  sería
sería 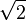 . Si elevamos
. Si elevamos  a la potencia
a la potencia  , obtenemos:
, obtenemos:
Como 2 es un número racional, hemos encontrado un ejemplo.
Esta prueba es no constructiva porque no nos dice cuál de los dos casos es el verdadero. Solo nos asegura que uno de ellos debe serlo, y en ambos casos, el teorema se cumple.
Pruebas constructivas: ¡Aquí está el ejemplo!
Una prueba constructiva para el teorema anterior (sobre potencias irracionales que dan un resultado racional) nos daría un ejemplo específico. Por ejemplo:
Aquí, 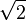 es irracional y 3 es racional.
es irracional y 3 es racional. 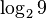 también es irracional. Si fuera racional, digamos
también es irracional. Si fuera racional, digamos  , entonces 9n sería igual a 2m. Pero 9n siempre es un número impar, y 2m (para m>0) siempre es un número par. Un número impar no puede ser igual a un número par, así que
, entonces 9n sería igual a 2m. Pero 9n siempre es un número impar, y 2m (para m>0) siempre es un número par. Un número impar no puede ser igual a un número par, así que 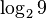 debe ser irracional.
debe ser irracional.
Otro ejemplo más complejo es el teorema del menor de un grafo. Este teorema dice que puedes dibujar un grafo (una red de puntos y líneas) en una forma de dona (un toro) si no tiene ciertas "piezas" prohibidas. Sin embargo, la prueba de que estas "piezas" existen no es constructiva, y aún no se sabe exactamente cuáles son.
Contraejemplos especiales
En la matemática constructiva, se puede demostrar que una afirmación es falsa dando un ejemplo que la contradice, igual que en las matemáticas normales. Pero también se puede usar un contraejemplo brouweriano para mostrar que una afirmación no es "constructiva".
Este tipo de contraejemplo muestra que la afirmación implica algo que se sabe que no se puede probar de forma constructiva. Por ejemplo, si una afirmación implica que "algo es o no es" sin una forma de saber cuál, entonces esa afirmación no es constructiva.
Galería de imágenes
Véase también
 En inglés: Constructive proof Facts for Kids
En inglés: Constructive proof Facts for Kids
- Constructivismo
- Teorema de existencia
- Método probabilístico