Inducción matemática para niños
La inducción matemática es una forma especial de razonamiento que se usa en matemáticas para demostrar que una afirmación o "proposición" es verdadera para una cantidad infinita de números. Imagina que tienes una fila muy larga de fichas de dominó. Si empujas la primera ficha y sabes que cada ficha, al caer, empujará a la siguiente, entonces todas las fichas caerán.
De manera similar, la inducción matemática funciona así:
- Primero, demuestras que la afirmación es cierta para el primer número (como la primera ficha de dominó).
- Luego, demuestras que si la afirmación es cierta para cualquier número, también lo será para el siguiente número.
Si logras hacer estas dos cosas, entonces la afirmación es verdadera para todos los números a partir del primero.
Este método se basa en un principio fundamental llamado el principio de la inducción matemática. Es como subir una escalera: si puedes subir el primer escalón y sabes que desde cualquier escalón puedes subir al siguiente, entonces puedes subir tan alto como quieras.
Contenido
Historia de la Inducción Matemática
Aunque la idea de la inducción matemática se ha usado desde hace mucho tiempo, no siempre se explicó de forma clara.
En la antigua Grecia, el filósofo Platón pudo haber usado una idea parecida en sus escritos alrededor del año 370 antes de Cristo. También, el matemático griego Euclides, en el siglo III antes de Cristo, usó un razonamiento similar para demostrar que hay infinitos números primos.
En la India, el matemático Bhaskara I también usó un método parecido en el siglo VII. Más tarde, alrededor del año 1000 después de Cristo, el matemático árabe Al-Karaji usó una forma de inducción para trabajar con secuencias de números y el teorema del binomio.
Sin embargo, la primera vez que alguien explicó claramente el principio de inducción fue el famoso filósofo y matemático francés Blaise Pascal en su libro Traité du triangle arithmétique (Tratado del triángulo aritmético) en 1665. Otros matemáticos como Fermat y Jakob Bernoulli también usaron ideas relacionadas.
Fue en el siglo XIX cuando matemáticos como George Boole, Augustus De Morgan, Charles Sanders Peirce, Giuseppe Peano y Richard Dedekind le dieron un tratamiento más completo y riguroso a la inducción matemática.
¿Cómo funciona una Demostración por Inducción?
Para demostrar una afirmación `P(n)` (donde `n` es un número) usando inducción, seguimos dos pasos principales:
El Caso Base
Primero, debes demostrar que la afirmación `P(n)` es verdadera para el primer valor posible de `n`. Este valor suele ser 1, pero a veces puede ser 0 o cualquier otro número, dependiendo de lo que quieras demostrar. Es como asegurarte de que la primera ficha de dominó realmente cae.
El Paso Inductivo
En este paso, asumes que la afirmación `P(n)` es verdadera para un número cualquiera `n` (a esto se le llama "hipótesis inductiva"). Luego, usando esa suposición, demuestras que la afirmación también debe ser verdadera para el siguiente número, `n+1`. Esto es como demostrar que si una ficha de dominó cae, la siguiente también caerá.
Si logras demostrar estos dos pasos, entonces la afirmación `P(n)` es verdadera para todos los números a partir del caso base.
Un Ejemplo Sencillo: La Suma de Números
Vamos a demostrar que la suma de los primeros `n` números naturales (1 + 2 + 3 + ... + `n`) siempre es igual a `n` multiplicado por `(n+1)` y luego dividido por 2. La fórmula es: 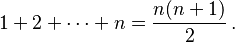
Paso 1: El Caso Base (n=1)
Primero, comprobamos si la fórmula funciona para el primer número, `n = 1`.
- El lado izquierdo de la fórmula es solo 1.
- El lado derecho es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1(1 + 1)}{2} = \frac{1 \cdot 2}{2} = 1 .
Como ambos lados son iguales (1 = 1), la fórmula es verdadera para `n = 1`. ¡El caso base está demostrado!
Paso 2: El Paso Inductivo (de k a k+1)
Ahora, vamos a suponer que la fórmula es verdadera para un número cualquiera `k`. Esto significa que: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 + 2 + \cdots + k = \frac{k(k + 1)}{2}\,. Esta es nuestra "hipótesis inductiva".
Nuestro objetivo es demostrar que, si esta hipótesis es cierta, entonces la fórmula también debe ser cierta para `k+1`. Es decir, queremos demostrar que: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1 + 2 + \cdots + k) + (k+1) = \frac{(k+1)((k+1) + 1)}{2}.
Empezamos con el lado izquierdo de esta nueva ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1 + 2 + \cdots + k) + (k+1)
Según nuestra hipótesis inductiva, sabemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 + 2 + \cdots + k es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{k(k + 1)}{2} . Así que podemos reemplazar esa parte: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{k(k + 1)}{2} + (k+1)
Ahora, vamos a simplificar esta expresión:
- Podemos sacar `(k+1)` como factor común:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (k+1) \left( \frac{k}{2} + 1 \right)
- Dentro del paréntesis, sumamos las fracciones:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (k+1) \left( \frac{k + 2}{2} \right)
- Esto es lo mismo que:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{(k+1)(k+2)}{2}
- Y podemos escribir `(k+2)` como `((k+1) + 1)`:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{(k+1)((k+1) + 1)}{2}
¡Hemos llegado exactamente al lado derecho de la fórmula para `k+1`! Esto demuestra que si la fórmula es verdadera para `k`, también lo es para `k+1`.
Como hemos demostrado el caso base y el paso inductivo, la fórmula Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 + 2 + \cdots + n = \frac{n(n + 1)}{2} es verdadera para todos los números naturales `n`.
Variantes de la Inducción
La inducción matemática tiene algunas variaciones que se usan dependiendo de la situación:
Caso Base Diferente
A veces, una afirmación no es cierta para todos los números naturales desde 1, sino solo a partir de un número específico (por ejemplo, desde 5). En ese caso, el "caso base" sería demostrar que la afirmación es cierta para ese número (en este ejemplo, para `n=5`). El paso inductivo seguiría siendo el mismo: si es cierto para `n`, es cierto para `n+1`, pero solo para `n` mayor o igual a 5.
Inducción Fuerte
En la "inducción fuerte", el paso inductivo es un poco diferente. En lugar de asumir que la afirmación es cierta solo para `n` para demostrarla para `n+1`, asumimos que la afirmación es cierta para *todos* los números menores o iguales a `n`. Con esta "hipótesis más fuerte", a veces es más fácil demostrar que la afirmación es cierta para `n+1`. Aunque se llama "fuerte", este método puede demostrar lo mismo que la inducción normal; simplemente ofrece otra forma de abordar la prueba.
El Principio del Buen Orden
La razón por la que la inducción matemática funciona se basa en una propiedad muy importante de los números naturales (los números enteros positivos, como 1, 2, 3, etc., o a veces incluyendo el 0). Esta propiedad se llama el "principio de buena ordenación":
Cualquier conjunto de números enteros no negativos que no esté vacío siempre tiene un elemento mínimo.
Esto significa que si tienes un grupo de números enteros positivos, siempre habrá uno que sea el más pequeño de todos. Este principio es fundamental para que la inducción matemática sea una herramienta de demostración válida.
Véase también
 En inglés: Mathematical induction Facts for Kids
En inglés: Mathematical induction Facts for Kids
- Recurrencia
- Número natural
- Axiomas de Peano


