Pentadecágono para niños
Datos para niños Pentadecágono |
||
|---|---|---|
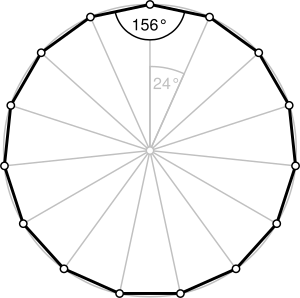
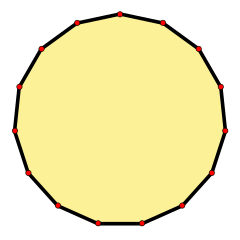 Un pentadecágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 15 | |
| Vértices | 15 | |
| Grupo de simetría |  , orden 2x15 , orden 2x15 |
|
| Símbolo de Schläfli | {15} (pentadecágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | 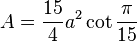 (lado  ) ) |
|
| Ángulo interior | 156° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un pentadecágono es una figura plana con 15 lados rectos y 15 puntos de esquina o vértices. Es un tipo de polígono, que son formas cerradas hechas de líneas rectas.
Contenido
¿Qué propiedades tiene un pentadecágono?
Un pentadecágono tiene 90 diagonales. Una diagonal es una línea que conecta dos vértices no adyacentes (que no están uno al lado del otro). Puedes calcular esto con una fórmula especial para polígonos.
La suma de todos los ángulos internos de cualquier pentadecágono siempre es 2340 grados. Esto significa que si sumas la medida de cada ángulo dentro de la figura, el total será 2340 grados.
¿Qué es un pentadecágono regular?
Un pentadecágono regular es un tipo especial de pentadecágono. En esta figura, todos sus lados miden lo mismo y todos sus ángulos internos son iguales.
Cada ángulo interno de un pentadecágono regular mide 156 grados. Esto es bastante grande, ¡casi un ángulo recto y medio! Cada ángulo externo (el ángulo que se forma al extender uno de sus lados) mide 24 grados.
¿Cómo se calcula el perímetro y el área?
El perímetro P de un pentadecágono regular se calcula multiplicando la longitud de uno de sus lados (llamémosla t) por el número de lados, que es 15.
- P = 15 × t
El área A de un pentadecágono regular se puede calcular con una fórmula que usa la longitud de su lado t. También se puede calcular si conoces la longitud de la apotema a, que es la distancia desde el centro del polígono hasta el punto medio de uno de sus lados.
- A = (Perímetro × apotema) / 2
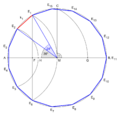
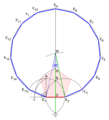
¿Cómo se puede construir un pentadecágono?
Un pentadecágono regular se puede dibujar usando solo una regla y compás. Esto es posible porque el número 15 se puede obtener multiplicando 3 y 5, que son números especiales llamados "números de Fermat".
Existen diferentes métodos para construir un pentadecágono. Uno de ellos es dibujarlo dentro de un círculo. Otro método es construirlo a partir de una longitud de lado ya conocida.
¿Qué es la simetría en un pentadecágono?
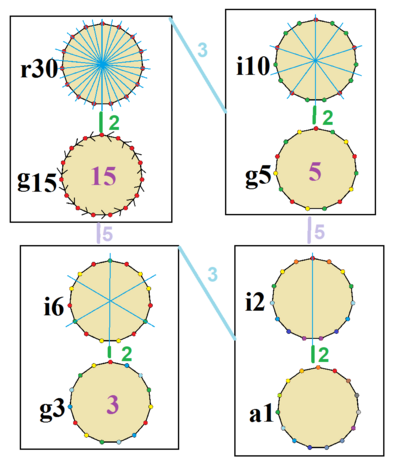
Un pentadecágono regular tiene mucha simetría. Esto significa que puedes girarlo o voltearlo y seguirá luciendo igual. Tiene 15 líneas de simetría, lo que significa que puedes doblarlo por esas líneas y las dos mitades coincidirán perfectamente. También tiene simetría de rotación, lo que significa que puedes girarlo y se verá igual en varias posiciones.
Hay diferentes tipos de simetrías que se pueden encontrar en los pentadecágonos, incluso en los que no son regulares.
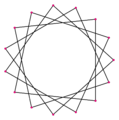
¿Qué son los pentadecagramas?
Los pentadecagramas son figuras con forma de estrella que se pueden crear usando los mismos 15 puntos (vértices) de un pentadecágono regular. En lugar de conectar cada punto con el siguiente, se saltan algunos puntos.
Hay varios tipos de pentadecagramas:
- Algunos son estrellas "regulares", como {15/2}, {15/4} y {15/7}. Esto significa que conectas cada segundo, cuarto o séptimo vértice, respectivamente.
- Otros son estrellas "compuestas", como {15/3}, {15/5} y {15/6}. Estas están formadas por la unión de polígonos más pequeños. Por ejemplo, {15/3} está hecha de tres pentágonos, y {15/5} está hecha de cinco triángulos equiláteros.
Galería de imágenes
Véase también
 En inglés: Pentadecagon Facts for Kids
En inglés: Pentadecagon Facts for Kids