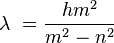Johann Jakob Balmer para niños
Datos para niños Johann Jakob Balmer |
||
|---|---|---|
 |
||
| Información personal | ||
| Nacimiento | 1 de mayo de 1825 Lausen (Suiza) |
|
| Fallecimiento | 12 de marzo de 1898 Basilea (Suiza) |
|
| Sepultura | Wolfgottesacker | |
| Nacionalidad | Suiza | |
| Educación | ||
| Educado en |
|
|
| Información profesional | ||
| Ocupación | Físico, matemático y profesor universitario | |
| Área | Matemáticas y física | |
| Empleador | Universidad de Basilea | |
Johann Jakob Balmer (nacido el 1 de mayo de 1825 en Lausen, Suiza y fallecido el 12 de marzo de 1898 en Basilea, Suiza) fue un importante matemático y físico suizo. Es conocido por crear una fórmula que ayuda a entender la luz que emite el átomo de hidrógeno.
Esta fórmula, llamada la fórmula de Balmer, es muy útil en la astronomía moderna. Permite a los científicos estudiar la luz de las estrellas y otros objetos en el espacio. Así, pueden aprender sobre cómo están hechos y cómo cambian con el tiempo. Sin esta fórmula, sería mucho más difícil encontrar hidrógeno en el cosmos y saber más sobre él.
Contenido
Johann Jakob Balmer: El Científico de la Luz
¿Quién fue Johann Jakob Balmer?
Johann Jakob Balmer fue el hijo mayor de un magistrado, que también se llamaba Johann Jakob Balmer, y de Elizabeth Rolle Balmer. Desde joven, mostró un gran talento para las matemáticas. Por eso, decidió estudiar esta materia en la universidad.
Estudió en la Universidad de Karlsruhe y en la Universidad de Berlín. En 1849, obtuvo su doctorado en la Universidad de Basilea. Su trabajo de doctorado fue sobre una curva matemática llamada cicloide. Después de terminar sus estudios, vivió el resto de su vida en Basilea. Allí, trabajó como profesor en una escuela para niñas y también en la Universidad de Basilea.
En 1868, cuando tenía 43 años, se casó con Christine Pauline Rinck. Tuvieron seis hijos juntos.
La Fórmula de Balmer: Descubriendo el Hidrógeno
Aunque Balmer era matemático, su descubrimiento más famoso no fue en matemáticas. Su gran aporte, que hizo a los sesenta años en 1885, fue una fórmula para entender las líneas de luz que se ven en el espectro del átomo de hidrógeno.
Un amigo, Eduard Hagenbach, le sugirió que estudiara este tema. Balmer usó las mediciones de las líneas de hidrógeno que había hecho otro científico, Anders Jonas Ångström. Con esos datos, Balmer creó su famosa fórmula de Balmer. Esta fórmula permite calcular la longitud de onda de la luz emitida por el hidrógeno:
En esta fórmula, n es igual a 2, h es un número fijo (3,6456 × 10−7 metros), y m puede ser 3, 4, 5, 6, y así sucesivamente.
Balmer llamó a h el "número fundamental del hidrógeno". Usó su fórmula para predecir una nueva línea de luz para m = 7. Poco después, le informaron que Ångström ya había observado esa línea con una longitud de onda de 397 nm. Otros científicos, Hermann Wilhelm Vogel y William Huggins, confirmaron que existían más líneas de la serie de Balmer en la luz de las estrellas blancas.
Más tarde, se descubrió que la fórmula de Balmer era un caso especial de una fórmula más general, la fórmula de Rydberg, creada por Johannes Rydberg. La explicación completa de por qué estas fórmulas funcionaban llegó en 1913, con el modelo atómico de Bohr de Niels Bohr.
La Importancia de la Fórmula de Balmer en la Astronomía
La fórmula de Balmer es muy importante para los astrónomos. Les ayuda a entender el universo de muchas maneras.
Estrellas y Galaxias
La serie de Balmer permite a los astrónomos saber si hay hidrógeno en las estrellas, nebulosas y otras partes de las galaxias. Como el hidrógeno es el elemento más común en el universo, conocer sus líneas de luz ayuda a saber de qué están hechos los objetos celestes.
También se usan las líneas de Balmer para medir el desplazamiento al rojo (redshift) de las galaxias. Cuando una galaxia se aleja de la Tierra, la luz que emite se estira y se ve más roja. Esto ayuda a los científicos a entender cómo se expande el universo y a qué velocidad se mueven las galaxias. Por ejemplo, al estudiar galaxias en el cúmulo de Coma, las líneas de Balmer ayudaron a confirmar la expansión del universo.
Las líneas de Balmer en la luz de una estrella también pueden decirnos su temperatura y de qué está hecha. Las estrellas muy calientes muestran líneas de Balmer más fuertes. Esto ayuda a clasificar las estrellas y entender cómo evolucionan.
Estudiar la luz de los átomos de hidrógeno en diferentes condiciones también ayuda a crear modelos de cómo funcionan las estrellas, nebulosas y galaxias. Las zonas donde nacen estrellas, como las nebulosas de emisión, muestran muchas líneas de Balmer. Esto da pistas sobre la actividad estelar y el ciclo de vida de las estrellas. Un ejemplo es la Nebulosa de Orión, donde las líneas de Balmer han sido clave para entender cómo se forman las estrellas jóvenes.
Exoplanetas y Agujeros Negros
Las líneas de Balmer también se han usado para estudiar las atmósferas de los exoplanetas (planetas fuera de nuestro sistema solar). Cuando un exoplaneta pasa por delante de su estrella, los astrónomos pueden analizar la luz que atraviesa su atmósfera. Así, pueden identificar hidrógeno y otros elementos, y saber cómo es el clima en esos planetas lejanos. Por ejemplo, en el exoplaneta KELT-9b, las líneas de Balmer ayudaron a detectar hidrógeno en su atmósfera extremadamente caliente.
Además, las líneas de Balmer han sido útiles para estudiar objetos cerca de los agujeros negros, como los discos de acreción. Analizando estas líneas, los científicos pueden aprender sobre los efectos de la gravedad extrema y las condiciones en esos discos, donde el material se calienta y emite luz. En el agujero negro supermasivo en el centro de la galaxia M87, las líneas de Balmer dieron información sobre el gas que lo rodea.
Reconocimientos y Legado
El trabajo de Johann Jakob Balmer ha sido reconocido de varias maneras:
- Las líneas de Balmer, la serie de Balmer y la constante de Balmer llevan su nombre.
- Un cráter en la Luna fue nombrado Balmer en su honor.
- El asteroide (12755) Balmer también lleva su nombre.
- La discontinuidad de Balmer es una característica en la luz de las estrellas que ayuda a los astrónomos a clasificarlas.
Galería de imágenes
-
Líneas espectrales del átomo de hidrógeno.
Véase también
 En inglés: Johann Jakob Balmer Facts for Kids
En inglés: Johann Jakob Balmer Facts for Kids