Heptadecágono para niños
Datos para niños Heptadecágono |
||
|---|---|---|
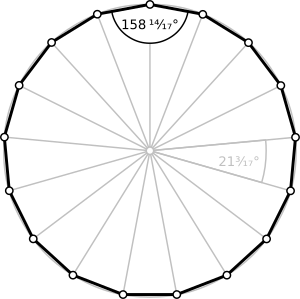
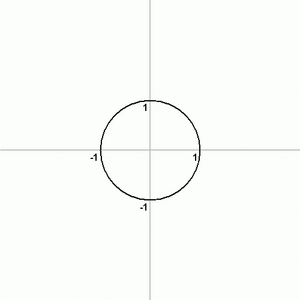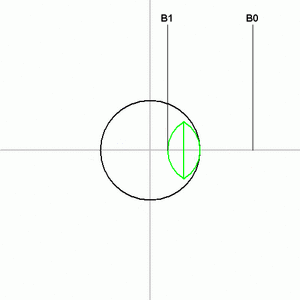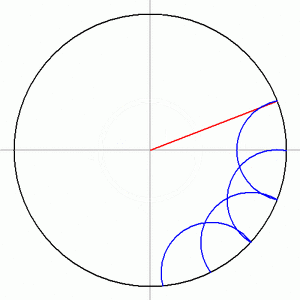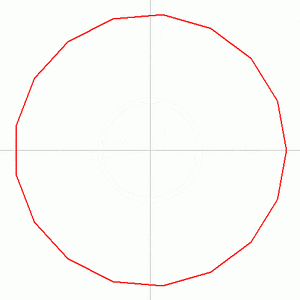
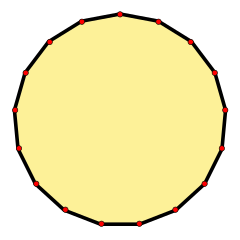 Un heptadecágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 17 | |
| Vértices | 17 | |
| Grupo de simetría | 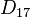 , orden 2x17 , orden 2x17 |
|
| Símbolo de Schläfli | {17} (heptadecágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | 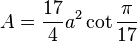 (lado  ) ) |
|
| Ángulo interior | 158+14/17° ≈ 158.8235294117647058 | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un heptadecágono es una figura plana que tiene 17 lados rectos y 17 esquinas. Es un tipo de polígono, que son formas cerradas hechas con líneas rectas.
Un hecho muy interesante sobre el heptadecágono es que el famoso matemático Carl Friedrich Gauss demostró que un heptadecágono regular (con todos sus lados y ángulos iguales) se puede dibujar usando solo una regla y compás. ¡Lo hizo cuando solo tenía 19 años! Este fue un gran avance en las matemáticas, ya que resolvió un problema que había existido desde la Grecia clásica.
Contenido
- El Heptadecágono: Una Figura de 17 Lados
- Galería de imágenes
- Véase también
El Heptadecágono: Una Figura de 17 Lados
¿Qué es un Heptadecágono?
Un heptadecágono es un polígono con 17 lados y 17 vértices. Los vértices son los puntos donde se unen dos lados. Como todos los polígonos, es una figura cerrada.
¿Cuántas Diagonales Tiene?
Una diagonal es una línea que conecta dos esquinas (vértices) de un polígono, pero que no es uno de sus lados. Un heptadecágono tiene 119 diagonales.
Podemos calcular esto con una fórmula sencilla:
- La fórmula es D = n(n-3)/2, donde 'n' es el número de lados.
- Para un heptadecágono, n = 17.
- Así, D = 17(17-3)/2 = 17(14)/2 = 238/2 = 119.
La suma de todos los ángulos internos de cualquier heptadecágono siempre es 2700 grados.
El Heptadecágono Regular: Lados y Ángulos Iguales
Un heptadecágono regular es especial porque todos sus 17 lados miden lo mismo y todos sus 17 ángulos internos son iguales.
- Cada ángulo interno de un heptadecágono regular mide aproximadamente 158.82 grados.
- Cada ángulo externo (el ángulo que se forma al extender uno de sus lados) mide aproximadamente 21.18 grados.
Cómo Calcular su Perímetro y Área
El perímetro de un heptadecágono regular es fácil de calcular. Solo tienes que multiplicar la longitud de uno de sus lados por 17 (el número total de lados).
- P = 17 × t (donde 't' es la longitud de un lado).
Para calcular el área de un heptadecágono regular, si conoces la longitud de uno de sus lados ('t'), puedes usar esta fórmula:
- A = (17 × t²) / (4 × tan(π/17))
- Aquí, π (pi) es una constante matemática (aproximadamente 3.14159) y tan es la función tangente.
Si conoces la longitud de la apotema ('a'), que es la distancia desde el centro del polígono hasta el punto medio de uno de sus lados, puedes usar esta otra fórmula para el área:
- A = (Perímetro × apotema) / 2 = (17 × t × a) / 2
El Descubrimiento de Gauss: Un Gran Avance
Carl Friedrich Gauss fue un matemático muy importante. Cuando tenía solo 19 años, en 1796, demostró que el heptadecágono regular se podía construir con regla y compás. Este fue un descubrimiento asombroso porque, durante más de 2000 años, nadie había logrado construir un polígono regular con un número de lados que no fuera 3, 4, 5, 6, 8, 10, 12, 15 o sus múltiplos por potencias de 2.
Se dice que Gauss quería que un heptadecágono regular fuera grabado en su lápida, pero el artesano no lo hizo porque era muy complicado y se parecería a un círculo.
¿Qué Significa "Construible con Regla y Compás"?
Significa que puedes dibujar la figura usando solo dos herramientas:
- Una regla (sin marcas de medida, solo para trazar líneas rectas).
- Un compás (para dibujar círculos y arcos).
Gauss demostró que un polígono regular es construible si el número de sus lados es un número de Fermat primo (como 3, 5, 17, 257, 65537) o un producto de estos números primos de Fermat distintos, multiplicado por cualquier potencia de 2. Como 17 es un número primo de Fermat, el heptadecágono es construible.
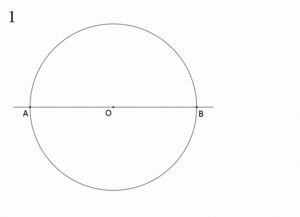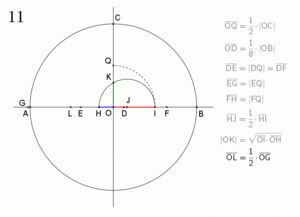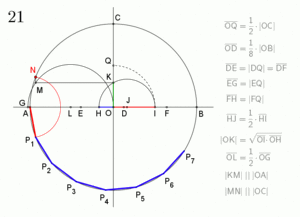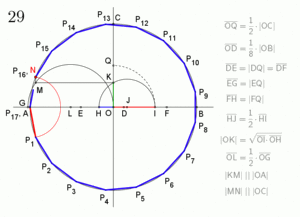
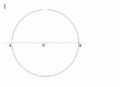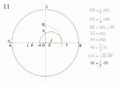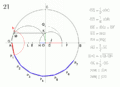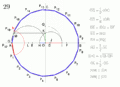
Cómo Construir un Heptadecágono Regular
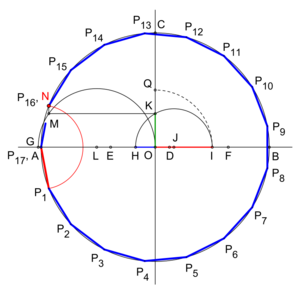
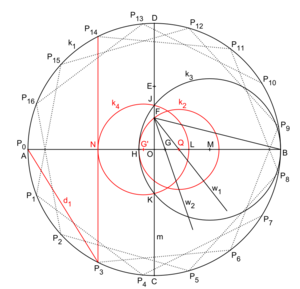
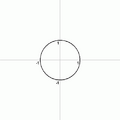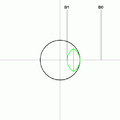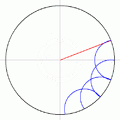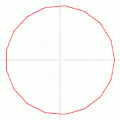
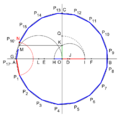
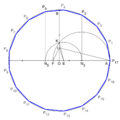
Aunque la idea matemática es compleja, se han desarrollado métodos para dibujar un heptadecágono regular. Uno de los más conocidos fue dado por Herbert William Richmond en 1893. Estos métodos usan una serie de pasos con regla y compás para encontrar los puntos exactos de los vértices.
Otro método de construcción fue descrito por T. P. Stowell en 1874.
Aquí hay otra construcción de Herbert William Richmond de 1893:
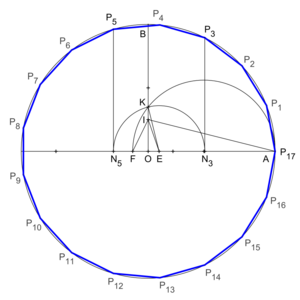
Y una variante de la construcción de Richmond:
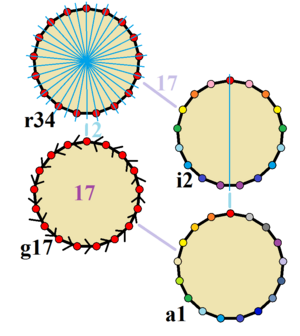
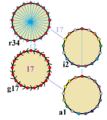
Simetría del Heptadecágono
Un heptadecágono regular tiene una simetría especial llamada simetría diedral. Esto significa que si lo giras o lo volteas, puede verse exactamente igual. Como 17 es un número primo, tiene un tipo de simetría muy específico.
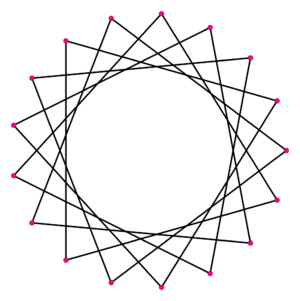
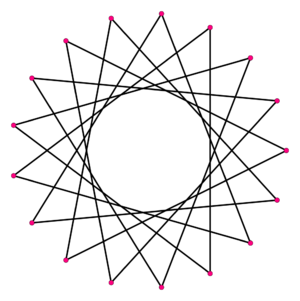
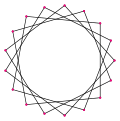
Heptadecagramas: Estrellas de 17 Puntas
Un heptadecagrama es una estrella que tiene 17 puntas. Se forman conectando los vértices de un heptadecágono regular de una manera específica, saltándose algunos vértices. Hay siete tipos diferentes de heptadecagramas regulares.
| Imagen | |||||||
|---|---|---|---|---|---|---|---|
| Ángulo interior | ≈137.647° | ≈116.471° | ≈95.2941° | ≈74.1176° | ≈52.9412° | ≈31.7647° | ≈10.5882° |
Galería de imágenes
Véase también
 En inglés: Heptadecagon Facts for Kids
En inglés: Heptadecagon Facts for Kids