Conjunto de Julia para niños

Los conjuntos de Julia son formas geométricas muy interesantes y complejas, que se repiten a sí mismas en diferentes escalas. Se les llama así en honor al matemático Gaston Julia, quien los estudió. Estos conjuntos se forman al analizar cómo se comportan ciertos números especiales, llamados números complejos, cuando se les aplica una operación matemática una y otra vez.

Imagina que tienes una regla matemática (una función) y un número. Aplicas la regla al número, luego aplicas la regla al resultado, y así sucesivamente. Los puntos que forman un conjunto de Julia son aquellos donde este proceso se vuelve "caótico" o impredecible. Es decir, los números resultantes saltan de un lado a otro sin un patrón claro.

Por otro lado, existe el conjunto de Fatou, nombrado por el matemático Pierre Fatou. Este conjunto incluye los puntos donde el proceso matemático es "estable" y predecible. Los puntos del conjunto de Fatou se quedan cerca unos de otros o siguen un patrón regular. El conjunto de Fatou es lo opuesto al conjunto de Julia.

Polinomios cuadráticos y cómo se forman

Una forma muy común de crear conjuntos de Julia es usando una operación matemática sencilla: elevar un número al cuadrado y luego sumarle otro número fijo. Esta operación se escribe como: 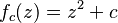, donde es un número complejo que elegimos al principio. El conjunto de Julia que se forma con esta operación se llama .

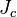Para saber si un punto pertenece a un conjunto de Julia, se sigue un proceso paso a paso:

• Empiezas con un número .
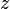• Luego, calculas el siguiente número usando la fórmula: .
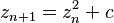• Repites este cálculo muchas veces.

Si los números que obtienes en esta secuencia se mantienen dentro de un límite (no se hacen infinitamente grandes), entonces el punto original 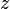pertenece al conjunto de Julia 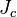. Si los números se disparan y se hacen enormes, entonces el punto no es parte del conjunto.

En las imágenes que ves, los puntos de color negro son los que pertenecen al conjunto de Julia. Los puntos de color no pertenecen. Los colores nos dicen qué tan rápido los números se hicieron grandes: los rojos oscuros se salieron del límite muy rápido, mientras que los blancos tardaron mucho más. Como no podemos hacer infinitos cálculos, se pone un límite de veces que se repite la operación. Si después de muchos cálculos el número sigue sin salirse del límite, se considera que el punto pertenece al conjunto.

Conjunto de Julia en 3D.

Se ha descubierto que si un número en la secuencia se hace más grande que 2 (su valor absoluto es mayor que 2), entonces ya sabemos que ese punto no pertenece al conjunto de Julia. Esto nos ayuda a saber rápidamente si un punto está o no en el conjunto.

Existe una conexión muy interesante entre los conjuntos de Julia y el conjunto de Mandelbrot. La relación es que un número pertenece al conjunto de Mandelbrot si y solo si el conjunto de Julia 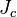que se forma con ese es una forma "conectada" (no tiene partes separadas).

Los conjuntos de Julia más llamativos y con formas más complejas aparecen cuando el número se elige en el borde del conjunto de Mandelbrot. Si está dentro del conjunto de Mandelbrot, el conjunto de Julia suele ser más simple, como un círculo, y solo sus bordes tienen esa apariencia fractal tan detallada. Por ejemplo, si , el conjunto de Julia es simplemente un círculo.

Los conjuntos de Julia se pueden crear con otras operaciones matemáticas más complejas, no solo con Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z^2 + c\, . También se pueden explorar en diferentes dimensiones o usando varias operaciones a la vez.

Ejemplos de Conjuntos de Julia

• 

  f(z) = z² + 0.279
• 

  f(z) = z³ + 0.400
• 

  f(z) = z⁴ + 0.484
• 

  f(z) = z⁵ + 0.544
• 

  f(z) = z⁶ + 0.590
• 

  f(z) = z⁷ + 0.626
• 

  f(z) = exp(z) - 0.65
• 

  f(z) = exp(z³) - 0.59
• 

  f(z) = exp(z³) - 0.621
  Zoom x9
• 

  f(z) = z * exp(z) + 0.04
• 

  f(z) = z² * exp(z) + 0.21
• 

  f(z) = z³ * exp(z) + 0.33
• 

  f(z) = z⁴ * exp(Z) + 0.41
• 

  f(z) = Sqr[Sinh(z²)] + (0.065,0.122i)
• 

  f(z) = [(z²+z)/Ln(z)] +(0.268,0.060i)
• 

  f(z) = Cosh(Z) +(-0.45,0.00i)
• 

  f(z) = Sin(Z) +(4.0,0.88i)

Véase también

En inglés: Julia set Facts for Kids

• Anexo:Fractales por dimensión de Hausdorff