Endecágono para niños
Datos para niños Endecágono |
||
|---|---|---|
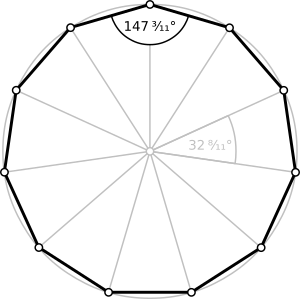
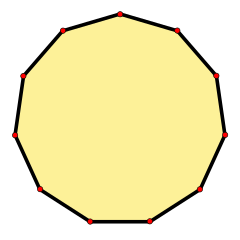 Un endecágono regular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 11 | |
| Vértices | 11 | |
| Diagonaless | 44 | |
| Grupo de simetría | 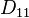 , orden 2x11 , orden 2x11 |
|
| Símbolo de Schläfli | {11} (endecágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | 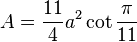 (lado (lado  ) ) |
|
| Ángulo interior | ≈147,273° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un endecágono o undecágono es una figura plana con once lados rectos y once vértices (puntos donde se unen los lados).
El nombre endecágono viene de las palabras griegas "hendeka" (que significa once) y "gono" (que significa esquina). A veces también se usa el término undecágono, que combina una palabra latina "undecim" (once) con la parte griega "gono".
Contenido
¿Qué es un Endecágono?
Un endecágono es un polígono que siempre tiene 11 lados y 11 vértices. No importa la forma que tenga, siempre tendrá estas características.
¿Cuántas Diagonales Tiene un Endecágono?
Un endecágono tiene 44 diagonales. Una diagonal es una línea que conecta dos vértices no consecutivos de un polígono. Puedes calcular el número de diagonales de cualquier polígono con una fórmula especial.
Para un polígono con n lados, la fórmula es: D = n(n-3)/2. Si sustituimos n por 11 (porque un endecágono tiene 11 lados), obtenemos: D = 11(11-3)/2 = 11(8)/2 = 88/2 = 44.
¿Cuál es la Suma de los Ángulos Interiores?
La suma de todos los ángulos internos de cualquier endecágono es siempre 1620 grados. Esto es igual a 9π radianes si usas esa unidad de medida.
Endecágono Regular: Lados y Ángulos Iguales
Un endecágono regular es un tipo especial de endecágono. En esta figura, todos sus lados miden lo mismo y todos sus ángulos internos son iguales.
Cada ángulo interno de un endecágono regular mide aproximadamente 147.27 grados. Cada ángulo externo (el ángulo que se forma al extender uno de sus lados) mide alrededor de 32.73 grados.
¿Se Puede Construir un Endecágono Regular con Regla y Compás?
No es posible dibujar un endecágono regular de forma perfecta usando solo una regla y un compás. Esto se debe a una propiedad matemática relacionada con el número 11. Sin embargo, se pueden hacer dibujos muy cercanos a un endecágono regular.
Algunos métodos más avanzados, como el "método neusis" o el "origami doble", sí permiten construirlo de forma exacta.
¿Cómo Calcular el Perímetro de un Endecágono Regular?
El perímetro es la medida del contorno de una figura. Para un endecágono regular, como todos sus lados son iguales, solo necesitas saber la longitud de uno de sus lados.
Si la longitud de un lado es t, el perímetro P se calcula multiplicando esa longitud por 11 (el número de lados): P = 11 × t
¿Cómo Calcular el Área de un Endecágono Regular?
El área es la medida de la superficie que cubre una figura. Para un endecágono regular, puedes calcularla de varias maneras.
Si conoces la longitud de un lado t, el área A se puede calcular con la siguiente fórmula: 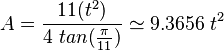 Aquí,
Aquí,  es la constante pi (aproximadamente 3.14159) y
es la constante pi (aproximadamente 3.14159) y 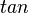 es la función tangente (una operación matemática que se usa en trigonometría).
es la función tangente (una operación matemática que se usa en trigonometría).
Otra forma de calcular el área es si conoces la longitud de la apotema a (la distancia desde el centro del polígono hasta el punto medio de uno de sus lados) y la longitud del lado t: 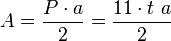 Donde P es el perímetro.
Donde P es el perímetro.
Construcciones Aproximadas de un Endecágono
Aunque no se puede construir un endecágono regular de forma perfecta con regla y compás, se han desarrollado métodos para hacer aproximaciones muy precisas.
Un ejemplo es el método descrito por T. Drummond en el año 1800. Este método permite dibujar un endecágono que es "suficientemente exacto para usos prácticos", es decir, muy, muy cercano a la forma ideal. Si dibujaras un endecágono de 10 metros de lado con este método, el error sería de solo unos 2.3 milímetros.
¿Dónde Vemos Endecágonos?
Los endecágonos no son tan comunes como los cuadrados o los triángulos, pero se pueden encontrar en algunos lugares interesantes.
Endecágonos en Monedas
Algunas monedas tienen formas que se parecen a un endecágono. Por ejemplo, la moneda de un dólar canadiense, conocida como loonie, tiene una forma que se asemeja a un endecágono. La moneda de dos rupias de la India también tiene una forma similar.
La moneda de un dólar de Susan B. Anthony de los Estados Unidos tiene un contorno endecagonal en el interior de sus bordes.
Formas Estrelladas de Endecágonos
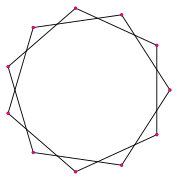
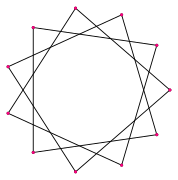
- Los cuatro endecágonos regulares estrellados
Así como existen polígonos regulares, también hay polígonos estrellados. Un endecágono estrellado es una figura con once puntas que se forma conectando los vértices de un endecágono regular de una manera específica, saltándose algunos vértices. Hay varias formas de hacer esto, creando diferentes patrones de estrellas.
Véase también
 En inglés: Hendecagon Facts for Kids
En inglés: Hendecagon Facts for Kids