Distribución de probabilidad para niños
La distribución de probabilidad es una herramienta matemática que nos ayuda a entender qué tan probable es que ocurran diferentes resultados en un evento. Imagina que lanzas una moneda o mides la altura de tus compañeros; la distribución de probabilidad nos dice cómo se espera que se repartan esos resultados.
En pocas palabras, es como un mapa que muestra las posibilidades de que algo suceda. Nos dice la probabilidad de que una variable (algo que puede cambiar de valor) tome un valor específico o esté dentro de un rango de valores.
La distribución de probabilidad se describe completamente con una "función de distribución". Esta función nos dice la probabilidad de que una variable sea menor o igual que un cierto número.
Contenido
¿Qué son las variables aleatorias?
Para entender las distribuciones, primero necesitamos saber qué es una variable aleatoria.
Tipos de variables aleatorias
- Variable aleatoria: Es un valor que obtenemos de un evento donde el resultado es incierto, es decir, depende del azar. Por ejemplo, el número que sale al lanzar un dado.
- Variable aleatoria discreta: Es aquella que solo puede tomar ciertos valores específicos, a menudo números enteros. Piensa en contar cosas, como el número de caras al lanzar una moneda varias veces. No puedes tener "2.5 caras".
- Variable aleatoria continua: Es aquella que puede tomar cualquier valor dentro de un rango. Piensa en medir cosas, como tu altura o el tiempo que tardas en correr. Puedes medir 1.65 metros o 1.657 metros.
¿Cómo se dividen las distribuciones de probabilidad?
Las distribuciones se dividen según el tipo de variable que estemos estudiando. Las dos categorías principales son:
Distribuciones discretas
Si la variable es discreta (toma valores enteros o contables), usamos una distribución discreta. Algunas de las más conocidas son:
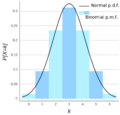
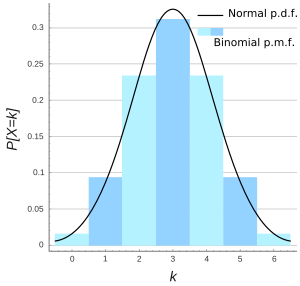
- Distribución binomial: Se usa cuando hay dos resultados posibles (como "sí" o "no", "éxito" o "fracaso") en una serie de intentos independientes. Por ejemplo, la probabilidad de obtener 3 caras en 5 lanzamientos de moneda.
- Distribución de Poisson: Describe el número de veces que ocurre un evento en un período de tiempo o en un espacio determinado. Por ejemplo, el número de llamadas que recibe un centro de atención en una hora.
- Distribución hipergeométrica: Se usa cuando sacamos elementos de un grupo sin devolverlos, y queremos saber la probabilidad de obtener un cierto número de elementos de una clase específica. Por ejemplo, sacar cartas de una baraja sin reemplazo.
A veces, podemos usar la distribución de Poisson para aproximar la binomial si tenemos muchos intentos y la probabilidad de éxito es muy pequeña.
Distribuciones continuas
Si la variable es continua (puede tomar cualquier valor en un rango), usamos una distribución continua. Algunos ejemplos importantes son:
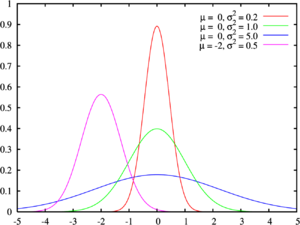
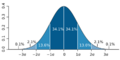
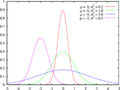
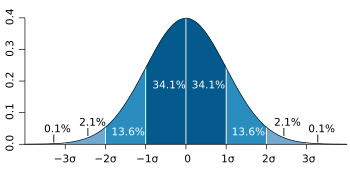
- Distribución normal o gaussiana: Es una de las más importantes y se ve como una "campana". Muchos fenómenos naturales, como la altura de las personas o los errores de medición, siguen esta distribución.
- Distribución exponencial: Describe el tiempo que pasa entre dos eventos consecutivos en un proceso donde los eventos ocurren de forma constante e independiente. Por ejemplo, el tiempo que tarda en fallar un componente electrónico.
¿Qué es la función de distribución?
La función de distribución, que se representa como F(x), nos da la probabilidad de que una variable aleatoria (X) sea menor o igual que un valor específico (x). En otras palabras, acumula las probabilidades hasta ese punto.
Características de la función de distribución
- Siempre va aumentando o se mantiene igual, nunca disminuye.
- Su valor siempre está entre 0 y 1.
- Cuando el valor de x es muy pequeño (tiende a menos infinito), la probabilidad es 0.
- Cuando el valor de x es muy grande (tiende a más infinito), la probabilidad es 1.
Si conocemos esta función, podemos calcular la probabilidad de que la variable esté en un rango determinado. Por ejemplo, la probabilidad de que X esté entre 'a' y 'b' es simplemente F(b) - F(a).
Más sobre las distribuciones discretas
Una distribución de variable discreta tiene una "función de masa de probabilidad" que nos dice la probabilidad de cada valor específico. La función de distribución para una variable discreta es la suma de las probabilidades de todos los valores hasta un punto dado.
Ejemplos de distribuciones discretas
- Distribución de Bernoulli: Es un caso muy simple de la binomial, donde solo hay un intento. Por ejemplo, el resultado de un solo lanzamiento de moneda (cara o cruz).
- Distribución uniforme discreta: Todos los valores posibles tienen la misma probabilidad de ocurrir. Un ejemplo clásico es el lanzamiento de un dado justo, donde cada número (1, 2, 3, 4, 5, 6) tiene la misma probabilidad de salir.
Más sobre las distribuciones continuas
Para las variables continuas, no podemos hablar de la probabilidad de un valor exacto (porque hay infinitos valores). En su lugar, usamos una "función de densidad de probabilidad". La función de distribución para una variable continua se calcula integrando esta función de densidad.
Ejemplos de distribuciones continuas
- Distribución uniforme continua: Similar a la discreta, pero para un rango continuo. Cualquier valor dentro de un intervalo dado tiene la misma probabilidad de ocurrir. Por ejemplo, el tiempo de espera de un autobús que pasa cada 10 minutos.
- Distribución beta: Se usa a menudo para modelar probabilidades o proporciones, ya que sus valores están entre 0 y 1.
- Distribución de Weibull: Se utiliza para describir la vida útil de productos o el tiempo hasta que ocurre un fallo.
- Distribución t de Student: Es útil cuando queremos estimar la media de una población pequeña y no conocemos su desviación estándar.
Galería de imágenes
-
La función de densidad de probabilidad de la distribución normal suele conocerse como la «campana de Gauss».
-
Gráfica de distribución binomial
Véase también
 En inglés: Probability distribution Facts for Kids
En inglés: Probability distribution Facts for Kids