Determinante (matemática) para niños
En matemáticas, el determinante es un número especial que se calcula a partir de una tabla cuadrada de números, llamada matriz. Este número nos da información importante sobre la matriz y sobre los problemas que representa.
Imagina que tienes un paralelogramo (una figura de cuatro lados con lados opuestos paralelos) o un paralelepípedo (una figura 3D como un ladrillo inclinado). El determinante puede decirte cuál es el "volumen" o "área" de estas figuras, incluso si están "torcidas" en el espacio. También es muy útil para saber si un sistema de ecuaciones tiene una solución única.
Contenido
Historia de los determinantes
Los determinantes se empezaron a usar en Occidente alrededor del siglo XVI, mucho antes que las matrices, que aparecieron en el siglo XIX. Sin embargo, en China, en un libro antiguo llamado Jiuzhang Suanshu, ya se usaban tablas de números y un método similar al que hoy conocemos como Eliminación de Gauss-Jordan.
El nombre "matriz" fue inventado por James Joseph Sylvester, quien quería dar a entender que las matrices eran como la "madre" de los determinantes.
Grandes matemáticos de los siglos siglo XVIII y siglo XIX ayudaron a desarrollar las propiedades de los determinantes. Muchos historiadores creen que la teoría de los determinantes comenzó con el matemático alemán Gottfried Leibniz en 1693, cuando los usó para resolver sistemas de ecuaciones. Pero algunos piensan que el matemático japonés Seki Kowa hizo algo similar unos años antes.
Augustin Louis Cauchy, un matemático francés, hizo muchas contribuciones importantes en 1812. Él demostró por primera vez una fórmula clave sobre cómo se comportan los determinantes cuando multiplicas matrices.
Otro matemático francés, Pierre-Simon Laplace, fue el primero en usar un método para calcular determinantes llamado "desarrollo por cofactores".
Carl Gustav Jakob Jacobi, un matemático alemán, fue quien hizo que la palabra "determinante" fuera ampliamente aceptada.
Primeros cálculos de determinantes
Al principio, el determinante se usaba para saber si un sistema de ecuaciones lineales tenía una solución única. En 1545, Gerolamo Cardano lo introdujo para sistemas de dos ecuaciones con dos incógnitas en su libro Ars Magna.
Los determinantes de órdenes más grandes tardaron más de cien años en aparecer. Curiosamente, el japonés Kowa Seki y el alemán Gottfried Leibniz encontraron los primeros ejemplos casi al mismo tiempo.
Leibniz estudió diferentes tipos de sistemas de ecuaciones. Como no tenía la notación de matrices que usamos hoy, representaba los números con dos índices. En 1678, trabajó con un sistema de tres ecuaciones y encontró una fórmula para calcular su determinante. Aunque no publicó este trabajo, sus ideas fueron redescubiertas más tarde.
En el mismo periodo, Kowa Seki publicó un manuscrito sobre determinantes. Parece que encontró fórmulas correctas para determinantes de orden 3 y 4. Sin embargo, sus descubrimientos no se difundieron mucho debido a que Japón estaba aislado del mundo exterior en ese momento.
Determinantes de cualquier dimensión
En 1748, Colin Maclaurin publicó una regla para resolver sistemas de ecuaciones con 2, 3 o 4 incógnitas usando determinantes. En 1750, Gabriel Cramer dio la regla general, aunque sin una demostración.
Matemáticos como Étienne Bézout y Alexandre-Théophile Vandermonde ayudaron a que los determinantes fueran más conocidos. En 1772, Pierre-Simon Laplace estableció reglas importantes para calcularlos. Al año siguiente, Joseph-Louis Lagrange descubrió la relación entre los determinantes y el cálculo de volúmenes.
Carl Friedrich Gauss usó por primera vez el término "determinante" en 1801. Lo aplicó a un concepto relacionado llamado discriminante.
Aparición de la noción moderna de determinante
Augustin Louis Cauchy fue el primero en usar el término "determinante" con el significado que le damos hoy. En 1812, publicó una demostración de la fórmula del determinante de un producto de matrices, lo que fue un gran avance.
En 1841, Carl Gustav Jakob Jacobi hizo que los determinantes fueran muy famosos con sus trabajos. Él presentó métodos sistemáticos para calcularlos. También definió el jacobiano, que es un tipo de determinante para funciones.
Arthur Cayley inventó la forma de escribir los determinantes con barras verticales en 1841 y también encontró la fórmula para calcular la matriz inversa usando determinantes en 1858.
¿Qué es un determinante? Volumen de figuras
Para entender qué es un determinante, podemos pensar en el volumen de figuras geométricas.
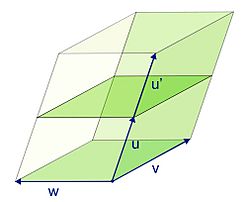
Imagina un paralelogramo en un plano (como un cuadrado o un rectángulo, pero inclinado). Este paralelogramo puede ser formado por dos vectores (flechas que tienen dirección y longitud). El determinante de estos dos vectores te dará el área de ese paralelogramo.
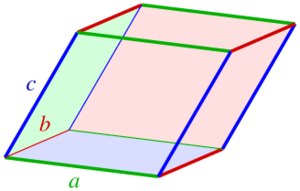
Si estás en un espacio 3D, puedes imaginar un paralelepípedo (como un ladrillo inclinado). Este paralelepípedo puede ser formado por tres vectores. El determinante de estos tres vectores te dará el volumen de ese paralelepípedo.
El determinante tiene algunas propiedades que se parecen a cómo se comportan las áreas y los volúmenes:
- Si "estiras" uno de los lados de tu figura (multiplicas un vector por un número), el área o volumen de la figura también se multiplica por ese número.
- Si dos de los vectores que forman tu figura son iguales, la figura se "aplana" y su volumen o área es cero.
El determinante generaliza esta idea de "volumen orientado". "Orientado" significa que el determinante puede ser positivo o negativo, lo que nos dice algo sobre la "dirección" o "sentido" de los vectores que forman la figura.
Determinante de una matriz
Ahora, hablemos del determinante de una matriz. Una matriz es una tabla cuadrada de números. Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=\left [ \begin{array}{cc} a & b \\ c & d \end{array} \right ]
Podemos pensar en las columnas de la matriz como si fueran vectores. Entonces, el determinante de la matriz es el determinante de esos vectores.
El determinante de una matriz 
se escribe como 
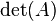o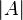 
.
Métodos de cálculo
La definición de determinante nos dice qué propiedades tiene, pero no nos da una fórmula directa para calcularlo. Sin embargo, existen varias formas de hacerlo.
Una forma general es el teorema de Laplace, que nos permite calcular un determinante grande dividiéndolo en varios determinantes más pequeños. Este proceso se repite hasta que llegamos a determinantes muy pequeños que son fáciles de calcular.
También existe la Fórmula de Leibniz para el cálculo de determinantes, que es una definición matemática más compleja. Aunque es importante para entender el determinante, no se usa mucho para calcularlo en la práctica si la matriz es muy grande, porque implica muchísimas operaciones.
Matrices de orden inferior
Para matrices pequeñas (de orden 1, 2 o 3), calcular el determinante es bastante sencillo.
- Matriz de orden 1:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \left [ \begin{array}{c} a_{11} \end{array} \right ] El determinante es simplemente el número: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \det A = a_{11}
- Matriz de orden 2:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \left [ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right ] El determinante se calcula así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): | A | = a_{11} a_{22} - a_{12} a_{21} Es decir, multiplicas los números en la diagonal principal y le restas la multiplicación de los números en la otra diagonal.
- Matriz de orden 3:
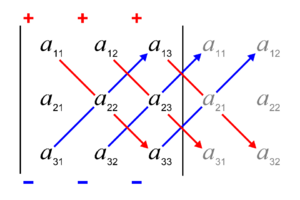
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \left [ \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right ] Para matrices de orden 3, se usa la regla de Sarrus, que es una forma fácil de recordar la fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A| = (a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32}) - (a_{31} a_{22} a_{13} + a_{32} a_{23} a_{11} + a_{33} a_{21} a_{12}) En resumen, sumas los productos de las diagonales que van de arriba izquierda a abajo derecha, y restas los productos de las diagonales que van de abajo izquierda a arriba derecha.
Determinantes de orden superior
Para matrices más grandes, como las de orden 4 o más, se sigue usando el teorema de Laplace. Esto significa que un determinante de orden 4 se convierte en 4 determinantes de orden 3, y así sucesivamente. Esto puede ser mucho trabajo. Por ejemplo, para un determinante de orden 10, tendrías que calcular muchísimos determinantes de orden 3.
Para hacer esto más fácil, a menudo se usa el Método de eliminación Gaussiana para transformar la matriz en una matriz triangular (una matriz donde todos los números por debajo o por encima de la diagonal principal son cero). El determinante de una matriz triangular es simplemente el producto de los números en su diagonal principal.
Primeros ejemplos: áreas y volúmenes
Como ya mencionamos, los determinantes están muy relacionados con el cálculo de áreas y volúmenes.
Determinante de dos vectores en el plano euclídeo
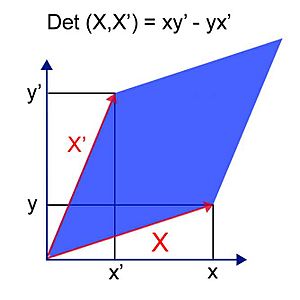
En un plano, si tienes dos vectores (flechas) X y X', el determinante de estos vectores se calcula con sus coordenadas: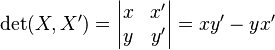 
Este número es el área del paralelogramo que forman los dos vectores. Si el determinante es cero, significa que los vectores están en la misma línea y no forman un paralelogramo (su área es cero). El signo del determinante te dice la "orientación" de los vectores.
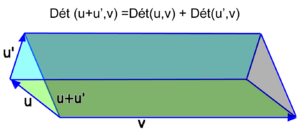
La figura 2 muestra cómo el determinante se comporta con la suma de vectores. Si tienes dos paralelogramos que comparten un lado, el área del paralelogramo grande que forman la suma de los lados es igual a la suma de las áreas de los dos paralelogramos pequeños.
Determinante de tres vectores en el espacio euclídeo
En un espacio 3D, si tienes tres vectores X, X y X, el determinante de estos vectores se llama producto mixto. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \det(X,X ',X '')=\begin{vmatrix} x & x' &x''\\ y & y'&y''\\ z&z'&z'' \end{vmatrix} El valor absoluto de este determinante es el volumen del paralelepípedo que forman los tres vectores. Si el determinante es cero, significa que los tres vectores están en el mismo plano y no forman un volumen (el paralelepípedo es "plano").
La figura 3 ilustra cómo el determinante se comporta con la suma de vectores en 3D, de manera similar al ejemplo de los paralelogramos.
Propiedades importantes
- El determinante de una matriz y el de su matriz traspuesta (la matriz que se obtiene al intercambiar filas por columnas) son iguales.
- Una aplicación lineal (una transformación que mueve puntos en el espacio de forma "recta") es "invertible" (es decir, se puede deshacer) si y solo si su determinante no es cero. Esto significa que una matriz tiene una inversa (se puede "deshacer") si y solo si su determinante es diferente de cero.
- Si intercambias dos columnas de una matriz, el signo de su determinante cambia.
Determinante del producto
Una propiedad muy importante es que el determinante del producto de dos matrices es igual al producto de sus determinantes. Si tienes dos matrices cuadradas A y B: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \det(\mathbf{AB}) = \det(\mathbf{A})\cdot\det(\mathbf{B}) Esto es muy útil para calcular determinantes y entender cómo se combinan las transformaciones que representan las matrices.
Menores de una matriz
Además del determinante de una matriz cuadrada, podemos definir los "menores" de una matriz. Un menor de orden r es el determinante de una submatriz cuadrada de rxr que se obtiene al elegir r filas y r columnas de la matriz original.
El rango de una matriz (que nos dice cuántas filas o columnas "independientes" tiene una matriz) coincide con el orden del menor más grande que no sea cero. Calcular menores es una forma común de encontrar el rango de una matriz.
Véase también
En inglés: Determinant Facts for Kids
- Matriz (matemática)
- Teorema de Laplace
- Regla de Sarrus
- Regla de Cramer
