Discriminante para niños
El discriminante es un número especial que nos ayuda a entender las soluciones de algunas ecuaciones matemáticas, especialmente las llamadas polinomios. Este número se calcula a partir de los números que acompañan a las letras en la ecuación (llamados coeficientes).
Si el discriminante es igual a cero, significa que la ecuación tiene soluciones que se repiten. Esto es muy útil para saber cómo se comportan las gráficas de estas ecuaciones.
Por ejemplo, para una ecuación cuadrática (que tiene un término con x al cuadrado) como: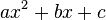 
su discriminante es: 
.
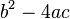Para una ecuación cúbica (que tiene un término con x al cubo) como: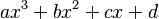 
su discriminante es: 
.
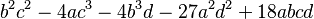El concepto de discriminante no solo se usa en polinomios, sino también en otras áreas de las matemáticas, como en las secciones cónicas (círculos, elipses, parábolas, hipérbolas) y en las formas cuadráticas.
Contenido
¿Qué es el Discriminante?
El discriminante es una herramienta matemática que nos da información clave sobre las raíces (o soluciones) de una ecuación. Es un valor numérico que se obtiene de los coeficientes de un polinomio. Su principal función es decirnos si las soluciones son números reales (los que usamos normalmente) o números complejos (que incluyen una parte imaginaria), y cuántas soluciones diferentes hay.
El Discriminante en Ecuaciones Cuadráticas
Las ecuaciones cuadráticas son muy comunes en matemáticas y tienen la forma Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^{2} + bx + c = 0 . El discriminante para estas ecuaciones se representa con la letra griega delta (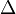
) y se calcula con la fórmula: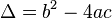 
Esta fórmula es la parte que está debajo de la raíz cuadrada en la fórmula general para resolver ecuaciones cuadráticas: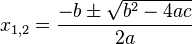 
.
¿Qué nos dice el Discriminante de una Ecuación Cuadrática?
El valor del discriminante nos da pistas importantes sobre las soluciones de una ecuación cuadrática:
- Si
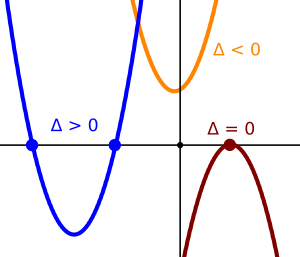
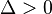(el discriminante es un número positivo), la ecuación tiene dos soluciones reales diferentes. Esto significa que la gráfica de la ecuación (que es una parábola) cruza el eje horizontal (eje X) en dos puntos distintos. - Si
(el discriminante es cero), la ecuación tiene una única solución real que se repite dos veces. En este caso, la gráfica de la parábola toca el eje horizontal en un solo punto, como si lo rozara. - Si
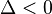(el discriminante es un número negativo), la ecuación no tiene soluciones reales. Sus soluciones son números complejos. Esto significa que la gráfica de la parábola nunca toca ni cruza el eje horizontal; se mantiene completamente por encima o por debajo de él.
El Discriminante en Otros Polinomios
Aunque la fórmula del discriminante se vuelve más complicada para polinomios de grados mayores (como los cúbicos o de cuarto grado), la idea principal sigue siendo la misma: el discriminante nos ayuda a saber si el polinomio tiene raíces (soluciones) que se repiten.
Para un polinomio general como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p(x)=a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0 el discriminante se puede calcular usando una matriz especial llamada matriz de Sylvester.
También se puede expresar el discriminante de un polinomio como: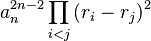 
donde Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): r_1, r_2, \ldots, r_n son las soluciones (raíces) del polinomio. Esta fórmula nos muestra claramente que el discriminante es cero si y solo si al menos dos de las soluciones son iguales.
El Discriminante en Figuras Geométricas (Secciones Cónicas)
El discriminante también se usa para identificar el tipo de sección cónica que representa una ecuación. Una sección cónica es una curva que se forma al cortar un cono con un plano (como un círculo, una elipse, una parábola o una hipérbola).
Para una ecuación de una sección cónica como: ax2 + bxy + cy2 + dx + ey + f= 0 el discriminante es: b2 − 4ac
Este valor nos dice qué forma tiene la sección cónica:
- Si el discriminante es menor que 0 (negativo), la ecuación describe una elipse o una circunferencia.
- Si el discriminante es igual a 0, la ecuación describe una parábola.
- Si el discriminante es mayor que 0 (positivo), la ecuación describe una hipérbola.
Galería de imágenes
-
Polinomios cuadráticos según su discriminante.
Véase también
En inglés: Discriminant Facts for Kids
