Medición para niños

Enciclopedia para niños

La medición es un proceso muy importante en la ciencia y en nuestra vida diaria. Consiste en comparar algo que queremos medir (como la longitud de una mesa o la temperatura del agua) con una unidad de medida que ya conocemos. Así, podemos saber cuántas veces esa unidad cabe en lo que estamos midiendo.

Por ejemplo, si quieres medir la longitud de tu lápiz, puedes usar una regla. La regla tiene unidades de medida como centímetros o milímetros. Al comparar el lápiz con la regla, descubres cuántos centímetros mide.

La medición es fundamental en el comercio, la tecnología y la investigación. A lo largo de la historia, las personas usaban diferentes sistemas de medición. Pero, a partir del siglo XVIII, se empezaron a crear sistemas más unificados y aceptados por todos. Esto llevó al Sistema Internacional de Unidades (SI), que es el que usamos hoy en día. Este sistema se basa en siete unidades principales para todas las medidas físicas. La ciencia que estudia la medición se llama metrología.

¿Cómo se mide?

Medir algo es como determinar su tamaño o cantidad. Imagina que quieres saber cuánto mide una mesa. Puedes usar una cinta métrica. La cinta tiene marcas que representan unidades de longitud, como metros o centímetros. Al usarla, comparas la mesa con esas unidades y obtienes un número. Ese número es la medida.

Cuando medimos, a veces el instrumento que usamos puede afectar un poco lo que estamos midiendo. Por eso, es importante ser cuidadoso para no cambiar demasiado el objeto o sistema que observamos.

Además, las medidas siempre tienen un pequeño margen de error. Esto puede ser por el instrumento que usamos o por la persona que mide. Por eso, a menudo se repiten las mediciones varias veces para obtener un resultado más preciso.

Medición directa

La medición directa es cuando usas un instrumento que compara directamente lo que quieres medir con un patrón.

Por ejemplo, si quieres saber la longitud de un libro, puedes usar una regla graduada. La regla ya tiene las unidades marcadas, y solo tienes que comparar el libro con esas marcas.
Otro ejemplo es medir la temperatura con un termómetro. El termómetro tiene una escala que te muestra directamente la temperatura.

Medición indirecta

A veces, no podemos medir algo directamente. Esto ocurre si el objeto es muy grande, muy pequeño o si no tenemos un instrumento para medirlo de forma directa. En estos casos, usamos la medición indirecta.

La medición indirecta consiste en medir otras cosas relacionadas y luego usar cálculos matemáticos para encontrar el valor que buscamos.

Ejemplo 1: Imagina que quieres saber la altura de un edificio muy alto. No puedes usar una cinta métrica para medirlo directamente desde arriba hasta abajo. Pero puedes medir la sombra del edificio en el suelo y la sombra de un objeto más pequeño (como un palo) que sí puedes medir. Con esos datos y un poco de matemáticas (usando la proporcionalidad), puedes calcular la altura del edificio.

Ejemplo 2: Para saber la temperatura de un líquido, a veces se usa un termopar. Este instrumento no mide la temperatura directamente, sino que detecta un pequeño cambio eléctrico que ocurre cuando sus cables metálicos entran en contacto con el líquido. Ese cambio eléctrico se convierte luego en un valor de temperatura.

Medidas que se pueden repetir

Una medida reproducible es aquella que puede ser repetida por diferentes personas y siempre se obtiene el mismo resultado, o uno muy parecido. Esto significa que el proceso de medición es confiable.

Por ejemplo, si mides el largo de tu escritorio varias veces con la misma regla, deberías obtener siempre el mismo resultado. Esto indica que la medida es reproducible.

Tipos de errores al medir

Cuando medimos, es normal que haya pequeños errores. Estos errores pueden ser de diferentes tipos:

Error sistemático
Error aleatorio

También podemos hablar de:

Error absoluto
Error relativo

Errores sistemáticos

Los errores sistemáticos son aquellos que se repiten de la misma manera cada vez que haces una medición. Son como un "fallo" constante en el instrumento o en el método. La buena noticia es que, como se repiten, a menudo se pueden corregir después.

Un ejemplo es una báscula que, incluso cuando no tiene nada encima, marca un peso pequeño. Ese es un error sistemático que siempre estará ahí a menos que se ajuste la báscula.

Errores aleatorios

Los errores aleatorios son impredecibles. No siguen un patrón y pueden variar en cada medición. Son más difíciles de corregir directamente, pero se pueden entender mejor si se hacen muchas mediciones y se usa la estadística.

Por ejemplo, si mides el tiempo que tarda una pelota en caer, pequeñas variaciones en tu reacción al iniciar o detener el cronómetro pueden causar errores aleatorios.

Error absoluto

El error absoluto es la diferencia entre el valor que mediste y el valor real (o el más exacto que se conoce). Se expresa con las mismas unidades que la medida.

Si mides algo y te da 10.2 cm, y el valor real es 10.0 cm, el error absoluto es 0.2 cm.

Error relativo

El error relativo es el error absoluto dividido por el valor real. Se puede expresar como un porcentaje. No tiene unidades.

Si el error absoluto es 0.2 cm y el valor real es 10.0 cm, el error relativo es 0.2 / 10.0 = 0.02, o 2%.

Calcular el error con estadística

Una forma de entender los errores es repetir la medición muchas veces. Si obtienes valores diferentes, significa que tu instrumento es lo suficientemente preciso para notar esas pequeñas variaciones.

En este caso, el valor más probable de la medición es el promedio de todas las medidas que tomaste. El error se puede estimar usando la desviación estándar, que te dice qué tan dispersos están tus resultados.

Nonio de un micrómetro, marcando la lectura 5,783 mm.

Unidades de medida

Las unidades de medida son los "patrones" que usamos para medir. Para que las mediciones sean útiles en todo el mundo, estas unidades deben cumplir ciertas condiciones:

Ser inalterables: No deben cambiar con el tiempo ni depender de quién las use.
Ser universales: Deben ser aceptadas y usadas por todos los países.
Ser fáciles de reproducir: Deben poder crearse o verificarse fácilmente en cualquier lugar.

El Sistema Internacional de Unidades (SI) es el sistema más usado. Fue adoptado en 1960 y busca ser un sistema universal y coherente. Sus unidades fundamentales son:

Longitud: Metro (m)
Masa: Kilogramo (kg)
Tiempo: Segundo (s)
Intensidad de corriente eléctrica: Amperio (A)
Temperatura: Kelvin (K)
Cantidad de sustancia: Mol (mol)
Intensidad luminosa: Candela (cd)

¿Qué es la teoría de la medición?

La teoría de la medición es el estudio de cómo medimos y qué significa medir. Hay diferentes formas de entenderla:

Enfoque clásico

En este enfoque, medir es comparar una cantidad con un patrón. Se usa mucho en ciencias como la física. Aquí, algo es "cuantitativo" (se puede medir con números) si es posible medirlo.

Enfoque representacional

Este enfoque dice que la medición es cuando relacionamos números con cosas que no son números. Por ejemplo, si asignamos un número a la altura de una persona, estamos haciendo una medición si esa asignación sigue ciertas reglas y refleja cómo se relacionan las alturas en el mundo real.

Teoría de la información

Esta teoría reconoce que todas las mediciones tienen un poco de incertidumbre. Para ellos, medir es hacer observaciones que nos ayudan a reducir esa incertidumbre. El resultado de una medición se expresa como una cantidad, pero siempre con un margen de error.

Mecánica cuántica

En el mundo de lo muy pequeño (como los átomos), la mecánica cuántica tiene una forma especial de ver la medición. Aquí, cuando mides una propiedad de una partícula, el acto de medir puede cambiar la partícula. Antes de medir, la partícula puede tener varios valores posibles, pero al medir, "elige" uno de ellos de forma aleatoria. Esto es una parte muy interesante y compleja de la física.

Herramientas para medir

Existen muchas herramientas para medir diferentes cosas:

Longitud

Regla: Para medir distancias cortas o dibujar líneas rectas.
Cinta métrica: Flexible, usada por carpinteros, sastres o en construcción para distancias más largas.
Calibradores: Para mediciones muy precisas de objetos pequeños.
Telémetros: Para medir distancias a objetos lejanos.

Tiempo

Relojes: Para medir períodos cortos (horas, minutos, segundos).
Calendarios: Para medir períodos largos (días, meses, años). El calendario gregoriano es el más común.
Cronómetros: Relojes muy precisos para medir intervalos de tiempo exactos.
Reloj atómico: El tipo de reloj más preciso que existe.

Masa

Básculas o balanzas: Para medir la masa de un objeto. Las balanzas comparan el objeto con masas conocidas hasta que se equilibran.

Temperatura

Termómetro: Mide la temperatura. La temperatura nos dice qué tan caliente o frío está algo.
Escalas de temperatura: Las más comunes son:

* Grados Celsius (°C): El agua se congela a 0°C y hierve a 100°C. * Grados Fahrenheit (°F): El agua se congela a 32°F y hierve a 212°F. * Kelvin (K): Es la unidad del Sistema Internacional, usada en ciencia. Su cero es el "cero absoluto", la temperatura más baja posible.

A partir de :	Kelvin	Celsius	Fahrenheit	Rankine	Réaumur
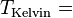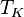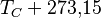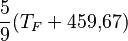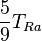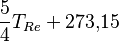$T_{\text{Kelvin}} =$	$T_K$	$T_C + 273{,}15$	$\frac{5} {9}(T_F + 459{,}67)$	$\frac{5} {9}T_{Ra}$	$\frac{5} {4}T_{Re} + 273{,}15$
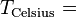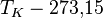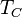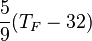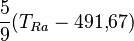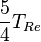$T_{\text{Celsius}} =$	$T_K - 273{,}15$	$T_C$	$\frac{5} {9}(T_F - 32)$	$\frac{5} {9}(T_{Ra} - 491{,}67)$	$\frac{5} {4}T_{Re}$
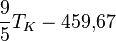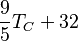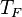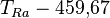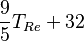$T_{\text{Fahrenheit}} =$	$\frac{9} {5}T_K - 459{,}67$	$\frac{9} {5}T_C + 32$	$T_F$	$T_{Ra} - 459{,}67$	$\frac{9} {5}T_{Re} + 32$
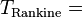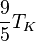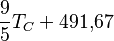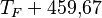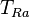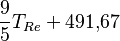$T_{\text{Rankine}} =$	$\frac{9} {5}T_K$	$\frac{9} {5}T_C + 491{,}67$	$T_F + 459{,}67$	$T_{Ra}$	$\frac{9} {5}T_{Re} + 491{,}67$
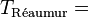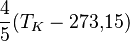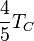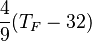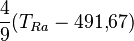$T_{\text{Réaumur}} =$	$\frac{4} {5}(T_K - 273{,}15)$	$\frac{4} {5}T_C$	$\frac{4} {9}(T_F - 32)$	$\frac{4} {9}(T_{Ra} - 491{,}67)$	$T_{Re}$

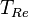Intensidad eléctrica

La corriente eléctrica es el movimiento de cargas eléctricas (generalmente electrones) a través de un material. La intensidad de la corriente eléctrica nos dice cuánta carga pasa por un punto en un tiempo determinado. Se mide en amperios (A).

Se usa un amperímetro para medir la corriente eléctrica.

Radiometría y fotometría

Estas áreas se encargan de medir la luz y la energía radiante.

Valor fotométrico	Símbolo	Unidad SI (símbolo)	Valor radiométrico	Símbolo	Unidad SI (símbolo)	Dimensión
Energía lumínica	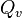$Q_v$	lumen por segundo	Energía radiante	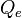$Q_e$	julio	M L² T⁻²
Flujo luminoso	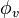$\phi_v$	lumen	Flujo radiante	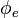$\phi_e$	watt	M L² T⁻³
Intensidad luminosa	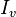$I_v$	candela	Intensidad radiante	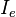$I_e$	watt por esterradián	M L² T⁻³
Luminancia	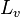$L_v$	candela por m²	Luminancia energética	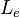$L_e$	watt por m² esterradián	M T⁻³
Iluminancia	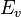$E_v$	lux	Iluminancia energética	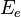$E_e$	watt por m²	M T⁻³
Emisión luminosa	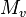$M_v$	lux o lumen por m²	Emitancia	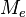$M_e$	watt por m²	M T⁻³
Exposición luminosa	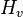$H_v$	lux por segundo	Exposición	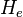$H_e$	julio por m²	M T⁻²

Galería de imágenes

Medición (del diámetro) con un calibre.

Ver también

Instrumento de medición
Metrología
Cantidad

Véase también

En inglés: Measurement Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Medición&oldid=4934540»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Medición para Niños. Enciclopedia Kiddle.