Nonio para niños
El nonio o escala de Vernier es una herramienta auxiliar que se encuentra en algunos instrumentos de medición. Su función principal es permitirnos realizar mediciones con mucha más exactitud. Imagina que tienes una regla normal; el nonio es como una pequeña regla extra que te ayuda a leer las divisiones más pequeñas de esa regla principal.
Contenido
¿Quién inventó el Nonio?
La idea original del nonio surgió en el siglo XVI gracias a un matemático, astrónomo y geógrafo portugués llamado Pedro Nunes. Él nació en Alcácer do Sal, Portugal, en 1492 y falleció en Coímbra en 1577. En 1514, Pedro Nunes inventó un sistema para medir longitudes y ángulos con mayor precisión, especialmente útil con un astrolabio. Su astrolabio tenía varias escalas paralelas que ayudaban a encontrar la medida más exacta.
Mucho tiempo después, en 1631, un matemático francés llamado Pierre Vernier (nacido en Ornans en 1580 y fallecido allí en 1637) desarrolló una escala similar para medir longitudes con gran precisión. Él publicó su trabajo en un libro.
Por eso, hoy en día, a esta escala se le llama tanto "nonio" (en honor a Pedro Nunes, cuyo nombre en latín era Petrus Nonius) como "vernier". Ambos términos se refieren a lo mismo y se usan en diferentes lugares, pero la idea original la aportó Pedro Nunes.
¿Cómo funciona el Nonio?
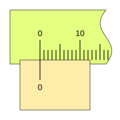
El nonio funciona junto con una regla principal. Esta regla tiene divisiones marcadas, como los milímetros en una regla escolar. Sobre esta regla se desliza una pieza móvil llamada "corredera" o "carro", que tiene el nonio grabado.
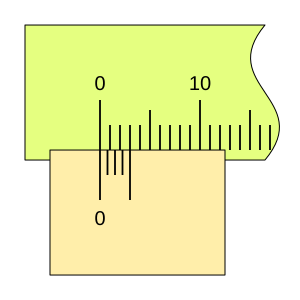
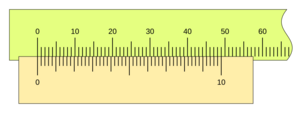
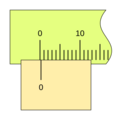
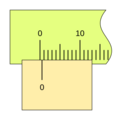
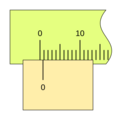
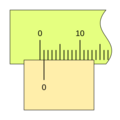
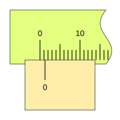
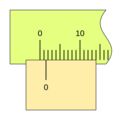
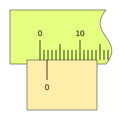
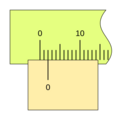
Imagina que quieres medir algo con una regla. Puedes ver fácilmente hasta la división más pequeña, por ejemplo, 1 milímetro. Pero, ¿qué pasa si la medida está entre dos milímetros, como 1.5 milímetros? Ahí es donde el nonio es útil.
El nonio toma un pequeño segmento de la regla principal y lo divide en un número mayor de partes. Por ejemplo, si el nonio toma 9 milímetros de la regla principal y los divide en 10 partes iguales, cada una de esas partes del nonio será un poco más pequeña que un milímetro (0.9 mm).
Cuando el nonio se mueve, una de sus divisiones se alineará perfectamente con una división de la regla principal. La posición del "cero" del nonio te da la medida entera (por ejemplo, los centímetros o milímetros completos), y la línea del nonio que coincide con una línea de la regla te indica la parte decimal o fraccionaria de la medida. Esto permite leer valores mucho más pequeños de lo que podrías ver solo con la regla principal.
Características del Nonio
Para entender mejor el nonio, hay algunas características importantes:
- u: Es la unidad más pequeña de la regla principal (por ejemplo, 1 milímetro).
- n: Es el número de divisiones que tiene el nonio.
- k: Es una constante que ayuda a diseñar el nonio, generalmente 1 o 2.
La apreciación (A) es la medida más pequeña que el nonio puede leer. Se calcula dividiendo la unidad de la regla (u) entre el número de divisiones del nonio (n).
- A = u / n
Por ejemplo, si la regla mide en milímetros (u = 1 mm) y el nonio tiene 10 divisiones (n = 10), la apreciación será 1 mm / 10 = 0.1 mm. Esto significa que puedes medir con una precisión de una décima de milímetro.
Lectura del Nonio
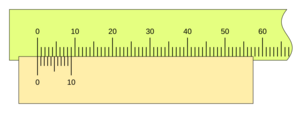
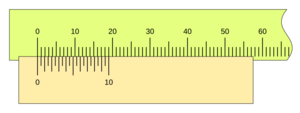
Para leer una medida con un nonio, sigue estos pasos: 1. Lee la parte entera: Observa la marca del cero (0) en el nonio. El número entero en la regla principal justo antes del cero del nonio es la parte entera de tu medida. 2. Lee la parte decimal: Busca la línea en el nonio que coincide exactamente con cualquier línea de la regla principal. El número de esa línea en el nonio (contando desde el cero) te dará la parte decimal de tu medida, multiplicada por la apreciación del nonio.
Por ejemplo, si el cero del nonio está después del 3 cm en la regla, y la 5ª línea del nonio coincide con una línea de la regla, y la apreciación es 0.1 mm, la medida sería 3 cm y 0.5 mm (o 30.5 mm).
Nonio de 10 divisiones
Este es uno de los nonios más comunes. Si la unidad de la regla es 1 mm y el nonio tiene 10 divisiones, su apreciación es 0.1 mm. Esto significa que puede medir con una precisión de una décima de milímetro. Es muy usado en muchos instrumentos.
Nonio de 20 divisiones
Otro nonio muy utilizado es el de 20 divisiones. Si la unidad de la regla es 1 mm y el nonio tiene 20 divisiones, su apreciación es 0.05 mm. Esto permite una precisión aún mayor, de cinco centésimas de milímetro.
Nonio de 50 divisiones
Este nonio ofrece una precisión muy alta. Con 50 divisiones y una unidad de regla de 1 mm, su apreciación es de 0.02 mm. Sin embargo, leer medidas tan pequeñas a simple vista puede ser difícil, ya que el ojo humano tiene un límite para distinguir detalles tan finos.
¿Para qué se usa el Nonio?
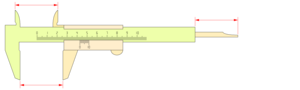
El nonio se usa en muchos instrumentos de medida para obtener lecturas muy precisas. El lugar donde más lo verás es en el calibre (también conocido como pie de rey). Este instrumento es muy popular por su bajo costo y su gran utilidad para medir objetos con mucha exactitud.
Un mismo calibre puede tener diferentes tipos de nonios, dependiendo de la precisión que se necesite. Gracias al nonio, el calibre es una herramienta muy versátil y práctica que se usa en muchos campos, desde talleres mecánicos hasta laboratorios.
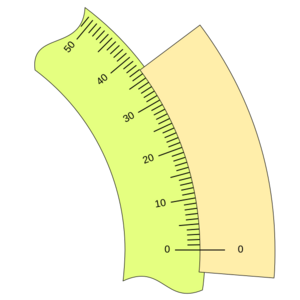
Nonio para medir ángulos
El nonio no solo se usa para medir longitudes, sino también para medir ángulos, por ejemplo, en grados, minutos y segundos. Un grado tiene 60 minutos, y un minuto tiene 60 segundos.
Si la unidad de la regla es 1 grado (u = 1°), y el nonio tiene un número de divisiones que sea divisor de 60 (como 12, 15, 20 o 30), podemos obtener una apreciación en minutos. Por ejemplo, un nonio con 12 divisiones puede medir con una precisión de 5 minutos (60 minutos / 12 divisiones = 5 minutos).
Galería de imágenes
-
Ejemplo de nonio en posición cero.
-
Nonio mostrando una pequeña medida.
-
Nonio mostrando una medida mayor.
-
Nonio mostrando una medida.
-
Nonio mostrando una medida.
-
Nonio mostrando una medida.
-
Nonio mostrando una medida.
-
Nonio mostrando una medida.
-
Nonio mostrando una medida.
-
Calibre con nonio.
-
Detalle de un nonio.
-
Calibre con nonio de alta precisión.
-
Detalle de un nonio de 50 divisiones.
-
Nonio en un instrumento de medición angular.
Véase también
En inglés: Vernier scale Facts for Kids
- Escala transversal
- Regla graduada
- Cinta métrica
- Transportador
- Goniómetro
- Calibre (instrumento)
- Micrómetro (instrumento)
