Sistema de coordenadas para niños
Un sistema de coordenadas es como un mapa especial que usa números para decirnos exactamente dónde está un punto o un objeto en el espacio. Imagina que quieres encontrar un tesoro: necesitas coordenadas para saber dónde cavar. En matemáticas, estas coordenadas son números que nos dan la ubicación precisa. El orden en que se escriben estos números es muy importante.
El estudio de los sistemas de coordenadas es parte de la geometría analítica. Esta rama de las matemáticas nos ayuda a resolver problemas de geometría usando números y ecuaciones.
Contenido
¿Qué son las coordenadas en geometría?
En geometría, las coordenadas son valores numéricos que nos dicen la posición de un punto en un plano (como una hoja de papel) o en el espacio (como tu habitación).
En un plano, la posición de un punto se puede encontrar midiendo su distancia a dos líneas rectas que se cruzan en un punto central llamado origen. Estas líneas se llaman ejes de coordenadas y se cruzan formando un ángulo recto (90 grados). Una de las coordenadas se llama ordenada y la otra abscisa.
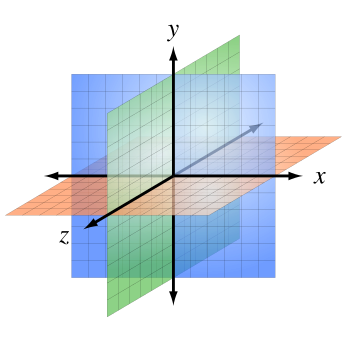
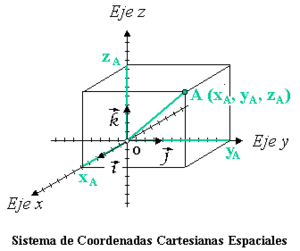
En el espacio tridimensional, la posición de un punto se determina midiendo su distancia a tres planos que se cruzan en el origen, también formando ángulos rectos entre sí. Este es el famoso sistema de coordenadas cartesianas.
Pero no son las únicas formas de ubicar un punto. También existen las coordenadas polares para el plano, que usan una distancia y un ángulo. Para el espacio, tenemos las coordenadas esféricas (que usan una distancia y dos ángulos) o las coordenadas cilíndricas (que usan una distancia, un ángulo y una altura). Estos sistemas son útiles porque a veces es más fácil describir un punto con ángulos que con solo distancias.
Coordenadas para ubicar lugares en la Tierra
En geografía, usamos un sistema de coordenadas similar a las esféricas para ubicar cualquier lugar en la Tierra. Este sistema usa:
- Latitud: Nos dice qué tan al norte o al sur está un punto con respecto al ecuador.
- Longitud: Nos dice qué tan al este o al oeste está un punto con respecto al meridiano de Greenwich.
- Altura: Nos indica la elevación de un punto sobre un nivel de referencia, como el nivel del mar.
Este sistema es fundamental para los mapas, la navegación y las tecnologías de GPS (Sistema de Posicionamiento Global), que nos ayudan a encontrar lugares en todo el mundo.
El sistema de coordenadas más común es el rectangular, también conocido como sistema de coordenadas cartesianas. Este sistema puede usarse para todo un espacio y los objetos dentro de él, siempre que tengamos un punto de partida llamado origen de coordenadas.
Existen muchísimas formas de definir coordenadas. Elegir el sistema adecuado puede hacer que resolver un problema matemático o físico sea mucho más sencillo.
Coordenadas en el espacio y las estrellas
En astronomía, usamos las coordenadas celestes para ubicar estrellas y otros objetos en el cielo. Son como un mapa del universo. Estas coordenadas son pares de ángulos, como la ascensión recta y la declinación.
Los astrónomos usan diferentes sistemas de coordenadas celestes, cada uno con un plano de referencia distinto. Por ejemplo, el sistema horizontal usa el horizonte como plano, el ecuatorial usa el ecuador celeste, y así sucesivamente.
Ejemplos de sistemas de coordenadas
Aquí te presentamos algunos de los sistemas de coordenadas más importantes y usados:
Sistema de coordenadas lineal
Imagina una línea recta infinita. En ella, podemos ubicar todos los números reales: los naturales, enteros, fracciones, decimales, etc. Cada punto de la recta representa un número.
Hay un punto especial en esta recta que representa el cero (0). Este es el punto de origen. A la derecha del origen están todos los números positivos, y a la izquierda, todos los números negativos.
Para representar un número en la recta, usamos letras mayúsculas y su coordenada. Por ejemplo, A(5) significa que el punto A está en el número 5.
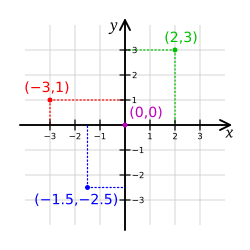
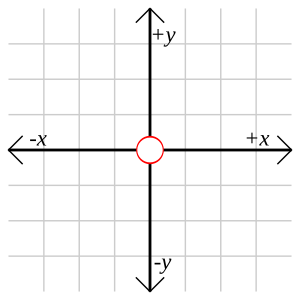
Sistema de coordenadas cartesianas
Este es el sistema más conocido. En un plano, se define por dos ejes que se cruzan en ángulo recto. En el espacio tridimensional, son tres ejes que se cruzan en ángulo recto.
Cada coordenada de un punto nos dice qué tan lejos está ese punto de los ejes. Por ejemplo, en un plano, un punto (x, y) significa que está a 'x' distancia del eje vertical y a 'y' distancia del eje horizontal.
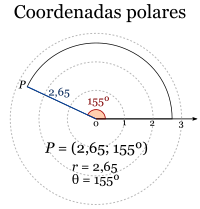
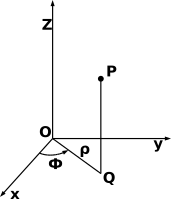
Sistema de coordenadas polares
Las coordenadas polares se usan en un plano. Para ubicar un punto, necesitamos una distancia y un ángulo.
Se elige un punto central llamado polo y una línea recta que sale de él, llamada eje polar. Para encontrar un punto, primero giramos desde el eje polar el ángulo que nos indican (en sentido contrario a las agujas del reloj). Luego, avanzamos la distancia indicada desde el polo a lo largo de esa línea.
Un mismo punto puede tener varias coordenadas polares. Por ejemplo, (r, θ), (r, θ+360°) y (-r, θ+180°) representan el mismo punto. El polo siempre se representa como (0, θ) para cualquier ángulo.
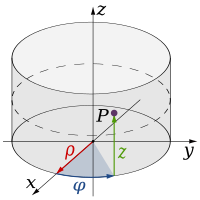
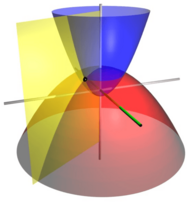
Sistema de coordenadas cilíndricas
Este sistema se usa para ubicar puntos en el espacio tridimensional. Es como una extensión de las coordenadas polares. Imagina un cilindro.
Para ubicar un punto, necesitamos tres valores:
- La distancia desde el eje central (como el radio de un cilindro).
- El ángulo que forma una línea desde el eje central con un eje de referencia (como en las polares).
- La altura del punto sobre un plano de referencia.
Es muy útil para problemas que tienen forma de cilindro o simetría alrededor de un eje.
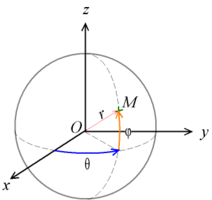
Sistema de coordenadas esféricas
También se usa en el espacio tridimensional. Imagina una esfera. Este sistema usa:
- La distancia desde el origen (el centro de la esfera) hasta el punto.
- Dos ángulos que nos dicen la dirección del punto, como la latitud y la longitud en la Tierra.
Es muy útil para describir objetos con forma de esfera o problemas con simetría esférica.
Coordenadas geográficas
Coordenadas geográficas Como mencionamos antes, son un tipo especial de coordenadas esféricas que usamos para la Tierra. Nos permiten ubicar cualquier lugar en la superficie terrestre usando latitud y longitud.
Se pueden mostrar en diferentes formatos:
- DD (Grados Decimales): Por ejemplo, 49.500, -123.500.
- DM (Grados:Minutos): Por ejemplo, 49:30.0, -123:30.0.
- DMS (Grados:Minutos:Segundos): Por ejemplo, 49:30:00, -123:30:00.
También existen otros sistemas de coordenadas geográficas proyectadas, como el sistema de coordenadas UTM, que se usan en mapas específicos.
Coordenadas homogéneas
Las coordenadas homogéneas son una forma especial de describir puntos, especialmente útil en infografía (gráficos por computadora) para representar escenas en 3D.
En este sistema, un punto en 2D (x, y) se representa con tres coordenadas (λx, λy, λ), donde λ (lambda) es un número diferente de cero. Esto permite representar puntos muy lejanos o "en el infinito".
Otros sistemas de uso común
Existen muchos otros sistemas de coordenadas, cada uno diseñado para problemas específicos:
- Coordenadas curvilíneas: Son una forma más general de coordenadas donde las líneas de referencia pueden ser curvas.
- Coordenadas log-polares: Usan el logaritmo de la distancia y un ángulo.
- Coordenadas baricéntricas (n-simplex): Se usan para analizar triángulos y centros de gravedad.
- Coordenadas biangulares: Definen un punto usando dos ángulos desde dos puntos fijos.
- Coordenadas bipolares: Basadas en círculos especiales.
- Coordenadas parabólicas: Usan parábolas como líneas de referencia.
Coordenadas de objetos geométricos
Los sistemas de coordenadas no solo sirven para puntos. También pueden usarse para ubicar objetos más complejos como líneas, planos, círculos o esferas. Por ejemplo, las coordenadas plückerianas nos ayudan a encontrar la posición de una línea recta en el espacio.
A veces, dos sistemas de coordenadas diferentes pueden ser equivalentes en su análisis. Se dice que son duales. Esto significa que los resultados de un sistema pueden aplicarse al otro, lo que se conoce como el principio de dualidad.
Cambios de coordenadas
En matemáticas y física, es muy común cambiar de un sistema de coordenadas a otro. Esto se hace para simplificar un problema. Imagina que tienes un problema que es muy difícil de resolver con coordenadas cartesianas, pero si lo cambias a coordenadas polares, se vuelve mucho más fácil.
Estas relaciones entre sistemas se describen con transformaciones de coordenadas. Son fórmulas que nos permiten convertir las coordenadas de un sistema a las de otro. Por ejemplo, para pasar de coordenadas polares (r, θ) a cartesianas (x, y) se usan las fórmulas: x = r * cos(θ) e y = r * sin(θ).
Curvas y superficies de coordenadas
En un sistema de coordenadas, si mantienes una coordenada fija y dejas que las otras varíen, obtendrás una curva de coordenadas. Por ejemplo, en coordenadas cartesianas, si fijas la 'x', obtendrás una línea recta vertical. Si fijas la 'y', obtendrás una línea recta horizontal. Por eso se les llama rectas coordenadas.
En otros sistemas, las curvas de coordenadas pueden ser realmente curvas. Por ejemplo, en coordenadas polares, si mantienes la distancia 'r' constante, obtendrás un círculo centrado en el origen.
En el espacio tridimensional, si mantienes una coordenada fija y dejas que las otras dos varíen, obtendrás una superficie de coordenadas. Por ejemplo, en coordenadas esféricas, si mantienes la distancia 'ρ' (rho) constante, obtendrás una esfera centrada en el origen. La intersección de dos superficies de coordenadas es una curva de coordenadas.
Origen de coordenadas
El origen de coordenadas es el punto de partida o referencia de un sistema de coordenadas. En este punto, el valor de todas las coordenadas suele ser cero. Por ejemplo, en un sistema cartesiano 2D, el origen es (0,0), y en 3D es (0,0,0).
Sin embargo, en algunos sistemas, no todas las coordenadas tienen que ser cero en el origen. Por ejemplo, en coordenadas esféricas, basta con que el radio sea cero (ρ = 0); los valores de los ángulos no importan.
En un sistema de coordenadas cartesianas, el origen es el punto donde se cruzan todos los ejes.
Galería de imágenes
-
El sistema de coordenadas esféricas se utiliza habitualmente en física. Asigna tres números (conocidos como coordenadas) a cada punto del espacio euclídeo: distancia radial r, ángulo polar θ y ángulo acimutal φ. El símbolo ρ se utiliza a menudo en lugar de "r"
Véase también
En inglés: Coordinate system Facts for Kids
- Coordenadas celestes
- Coordenadas geográficas
- Regla de la mano derecha
- Tabla en coordenadas cilíndricas y esféricas
