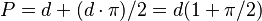Perímetro para niños
En geometría, el perímetro es la medida del contorno o el borde de una figura. Imagina que quieres poner una cerca alrededor de un jardín; la longitud de esa cerca sería el perímetro del jardín. Para figuras planas como triángulos o cuadrados, el perímetro se calcula sumando la longitud de todos sus lados. Cuando hablamos del contorno de figuras curvas, como un círculo, lo llamamos circunferencia. El perímetro es muy útil en campos como la arquitectura y la ingeniería para definir límites y espacios.
Contenido
¿Para qué sirve el Perímetro?
El perímetro es una herramienta clave en el estudio de las figuras geométricas. Nos ayuda a calcular la longitud del "borde" de un objeto. Por ejemplo, si quieres saber cuánta valla necesitas para rodear un terreno, ¡usas el perímetro! Tiene muchas aplicaciones prácticas:
- Construcción: Para saber cuántos materiales se necesitan para cercas, muros o para organizar espacios en edificios.
- Agricultura: Para determinar la longitud de las cercas o los sistemas de riego en los campos de cultivo.
- Deportes: Para definir el tamaño de los campos de juego o las rutas de carrera.
- Diseño: Para calcular los materiales necesarios para empaques o partes de productos.
- Geografía: Para marcar límites de áreas o territorios en los mapas.
- Educación: Es fundamental para resolver problemas de matemáticas y aprender geometría.
- Turismo: Para planificar rutas de senderismo o recorridos en parques.
Polígonos y su Perímetro
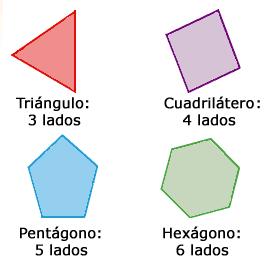
Un polígono es una figura cerrada formada por varias líneas rectas que se unen. Estas líneas solo se tocan en sus extremos y no se cruzan. Piensa en un triángulo, un cuadrado o un pentágono; todos son polígonos. Están hechos de al menos tres puntos unidos por líneas rectas.
Un polígono regular es especial porque todos sus lados miden lo mismo y todos sus ángulos son iguales. Son muy importantes para calcular perímetros. Esto se debe a que son las formas más sencillas y, además, el perímetro de muchas otras formas se puede calcular aproximándolas con polígonos regulares.
Un matemático muy famoso llamado Arquímedes usó esta idea. Él calculó el perímetro de un círculo rodeándolo con polígonos regulares cada vez con más lados.
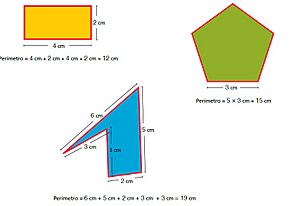
El perímetro de cualquier polígono se calcula sumando las longitudes de todos sus lados. Por ejemplo, el perímetro de un rectángulo con un ancho de a y un largo de l es igual a  .
.
Si un polígono tiene todos sus lados de la misma longitud (es decir, es equilátero), para calcular su perímetro solo tienes que multiplicar la longitud de uno de sus lados por el número total de lados.
La Apotema: Una Ayuda para Polígonos Regulares
La apotema es una línea especial en los polígonos regulares. Va desde el centro del polígono hasta el punto medio de uno de sus lados, formando un ángulo recto (90 grados) con ese lado. Es muy útil para calcular el área de los polígonos regulares.
¿Cómo se usa la Apotema?
La apotema se usa en una fórmula para calcular el área de un polígono regular:
Área = (Perímetro × Apotema) / 2
El perímetro es la suma de todos los lados, y la apotema es esa distancia desde el centro al punto medio de un lado. En un polígono regular, todos los lados y ángulos son iguales. La apotema también nos ayuda a entender cómo se relaciona el polígono con un círculo que se puede dibujar justo dentro de él.
Fórmulas de la Apotema
Para calcular la apotema de un polígono regular con n lados y una longitud de lado l, puedes usar esta fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a = \frac{l}{2 \cdot \tan(\frac{\pi}{n})}
Donde:
- a es la apotema.
- l es la longitud de un lado del polígono.
- n es el número de lados del polígono.
La apotema es clave para resolver problemas de áreas y perímetros. También se usa en la arquitectura y el diseño para crear figuras simétricas y estructuras, ya que ayuda a entender mejor sus propiedades geométricas.
Cálculo del Perímetro de Figuras Comunes
Perímetro de un Polígono
Para calcular el perímetro de cualquier polígono, simplemente sumas las longitudes de todos sus lados.
- Para un triángulo: P = a + b + c (donde a, b y c son las longitudes de sus tres lados).
- Para un cuadrilátero (figura de cuatro lados): P = a + b + c + d.
En general, para un polígono con n lados, la fórmula es:
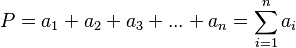
Aquí, n es el número de lados y 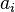 es la longitud de cada lado.
es la longitud de cada lado.
Si el polígono es equilátero o regular (todos sus lados son iguales):
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P = n \cdot a
Donde n es el número de lados y a es la longitud de un lado.
Perímetro de un Círculo (Circunferencia)
El perímetro de un círculo se llama circunferencia. Se calcula con la siguiente fórmula:
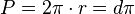
Donde:
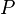 es la longitud del perímetro (circunferencia).
es la longitud del perímetro (circunferencia).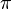 es la constante matemática pi (aproximadamente 3.14159).
es la constante matemática pi (aproximadamente 3.14159). es la longitud del radio (la distancia del centro al borde del círculo).
es la longitud del radio (la distancia del centro al borde del círculo).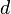 es la longitud del diámetro (la distancia de un lado a otro del círculo, pasando por el centro, que es el doble del radio).
es la longitud del diámetro (la distancia de un lado a otro del círculo, pasando por el centro, que es el doble del radio).
Para obtener el perímetro de un círculo, multiplicas el diámetro por el número π.
Perímetro de un Semicírculo
Un semicírculo es la mitad de un círculo. Su perímetro está formado por la mitad de la circunferencia y una línea recta que es el diámetro. Por eso, su perímetro es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P = 2r + r \cdot \pi = r ( 2 + \pi )
o
Donde:
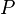 es la longitud del perímetro.
es la longitud del perímetro.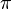 es la constante matemática pi (aproximadamente 3.14159).
es la constante matemática pi (aproximadamente 3.14159). es la longitud del radio.
es la longitud del radio.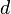 es la longitud del diámetro.
es la longitud del diámetro.
Fórmulas Generales del Perímetro
| Forma | Fórmula | Variables |
|---|---|---|
| círculo |  |
donde  es el radio del círculo y es el radio del círculo y 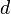 es el diámetro. es el diámetro. |
| triángulo | 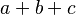 |
donde  , ,  y y  son las longitudes de los lados del triángulo. son las longitudes de los lados del triángulo. |
| cuadrado/rombo | 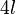 |
donde 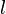 es la longitud del lado. es la longitud del lado. |
| rectángulo | 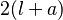 |
donde 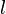 es el largo y es el largo y  el ancho. el ancho. |
| polígono equilátero | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n \cdot l\, | donde  es el número de lados y es el número de lados y 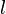 es la longitud de uno de los lados. es la longitud de uno de los lados. |
| polígono regular | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n \cdot l\, | donde  es el número de lados y es el número de lados y 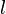 es la longitud de uno de los lados. es la longitud de uno de los lados. |
| polígono | 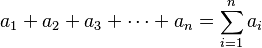 |
donde 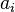 es la longitud del lado es la longitud del lado  (1.º, 2.º, 3.º ... n-ésimo) lado de un polígono de n lados. (1.º, 2.º, 3.º ... n-ésimo) lado de un polígono de n lados. |
Véase también
 En inglés: Perimeter Facts for Kids
En inglés: Perimeter Facts for Kids
- Circunferencia
- Teorema de Pitágoras
- Geometría
- Plano
- Polígono regular
- Polígono irregular
- Área
- Polígono