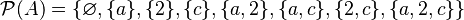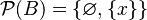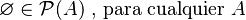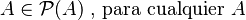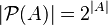Conjunto potencia para niños
En matemáticas, el conjunto potencia de un conjunto es como una "colección de colecciones". Imagina que tienes un grupo de cosas; el conjunto potencia es un nuevo grupo que contiene todas las formas posibles de agrupar esas cosas, incluyendo no agrupar ninguna (el conjunto vacío) y agruparlas todas.
Por ejemplo, si tienes un conjunto llamado A con los números 1, 2 y 3:
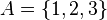
El conjunto potencia de A, que se escribe como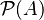 
, sería:
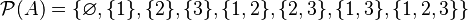
Aquí,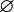 
representa el conjunto vacío, es decir, un grupo sin ningún elemento.
El conjunto potencia de 
también se conoce como el conjunto de las partes de . La cantidad de elementos que tiene el conjunto potencia se calcula con una fórmula especial: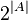 
, donde 
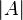es el número de elementos del conjunto original .
Contenido
¿Qué es el Conjunto Potencia?
El conjunto potencia de un conjunto es el conjunto que incluye todos los subconjuntos posibles de . Un subconjunto es un grupo de elementos que pertenecen al conjunto original.
- Ejemplos sencillos
- Si tienes el conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \{a, 2, c\} , su conjunto potencia es:
- Si el conjunto
solo tiene un elemento, por ejemplo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): B = \{x\} , su conjunto potencia es:
Propiedades Importantes
El conjunto potencia tiene algunas características interesantes:
- El conjunto vacío (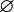) siempre es parte del conjunto potencia de cualquier conjunto. Esto significa que siempre puedes formar un grupo sin elementos.
- El conjunto original () siempre es uno de los subconjuntos en su propio conjunto potencia. Esto significa que puedes formar un grupo con todos los elementos del conjunto original.
¿Cuántos elementos tiene el Conjunto Potencia?
El número de elementos en el conjunto potencia se llama su número cardinal. Para un conjunto finito (un conjunto con un número limitado de elementos), el cardinal del conjunto potencia se calcula elevando el número 2 a la potencia del número de elementos del conjunto original.
Si el conjunto tiene 
elementos, entonces el número de elementos en su conjunto potencia es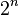 
.
|
Por ejemplo, si el conjunto tiene 3 elementos (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{1, 2, 3\} ), entonces su conjunto potencia tendrá Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^3 = 2 \times 2 \times 2 = 8 elementos, como vimos en el primer ejemplo.
Esta relación es la razón por la que a veces se usa la notación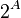 
para referirse al conjunto potencia.
Para los conjuntos infinitos, la idea es similar: el conjunto potencia de un conjunto infinito siempre tiene más elementos que el conjunto original. Esto es una idea importante en matemáticas que nos ayuda a entender los diferentes "tamaños" de los infinitos.
- El conjunto potencia del conjunto vacío (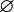) tiene solo un elemento, que es el propio conjunto vacío. Esto se calcula como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^0 = 1 .
Axioma del Conjunto Potencia
En la teoría de conjuntos, que es una rama de las matemáticas que estudia los conjuntos, la existencia del conjunto potencia se establece mediante un "axioma". Un axioma es una regla básica que se acepta como verdadera sin necesidad de demostración. Este axioma es importante porque permite trabajar con conjuntos muy grandes, incluso con aquellos que tienen un número infinito de elementos.
Véase también
En inglés: Power set Facts for Kids
