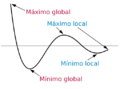
Extremos de una función para niños
En matemáticas, los máximos y mínimos de una función son puntos muy importantes. Imagina la gráfica de una función como una montaña rusa. Los máximos son las cimas más altas y los mínimos son los valles más bajos.
Estos puntos se conocen como extremos de una función. Pueden ser los valores más grandes (máximos) o más pequeños (mínimos) que la función alcanza. Un extremo puede estar en una parte específica de la gráfica (llamado extremo local o relativo) o en toda la gráfica de la función (llamado extremo global o absoluto).
Encontrar estos valores extremos es una parte fundamental de la optimización matemática. Esto significa buscar la mejor solución o el mejor valor posible en un problema.
Extremos de una Función: Máximos y Mínimos
¿Qué son los Extremos de una Función?
Los extremos de una función son los puntos donde la función alcanza su valor más alto o más bajo. Piensa en la trayectoria de una pelota lanzada al aire: el punto más alto que alcanza es un máximo. Si la pelota cae en un hoyo, el fondo del hoyo sería un mínimo.
Estos puntos son cruciales para entender cómo se comporta una función. Nos ayudan a saber dónde la función "sube" o "baja" y dónde cambia de dirección.
Extremos Locales o Relativos
Un máximo local (o relativo) es como la cima de una pequeña colina en un paisaje montañoso. Es el punto más alto en una región específica de la gráfica, pero puede haber puntos más altos en otras partes de la función.
Matemáticamente, si tenemos una función  y un punto
y un punto 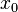 , decimos que
, decimos que 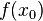 es un máximo local si los valores de la función alrededor de
es un máximo local si los valores de la función alrededor de 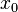 son menores o iguales que
son menores o iguales que 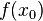 . Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) \le f(x_0) para los puntos cercanos a
. Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) \le f(x_0) para los puntos cercanos a 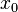 .
.
De manera similar, un mínimo local (o relativo) es como el fondo de un pequeño valle. Es el punto más bajo en una región específica de la gráfica, aunque puede haber puntos más bajos en otras partes de la función.
Para un mínimo local, los valores de la función alrededor de 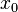 son mayores o iguales que
son mayores o iguales que 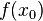 . Esto significa
. Esto significa 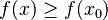 para los puntos cercanos a
para los puntos cercanos a 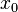 .
.
Extremos Globales o Absolutos
Un máximo absoluto es el punto más alto de toda la gráfica de la función. Es la cima más alta de todo el paisaje, sin importar dónde mires.
Si 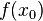 es un máximo absoluto, significa que para cualquier otro punto
es un máximo absoluto, significa que para cualquier otro punto  en el dominio de la función, el valor de la función en
en el dominio de la función, el valor de la función en  siempre será menor o igual que
siempre será menor o igual que 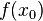 . Se escribe así:
. Se escribe así:
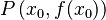 máximo absoluto de
máximo absoluto de 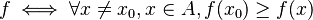 .
.
Un mínimo absoluto es el punto más bajo de toda la gráfica de la función. Es el valle más profundo de todo el paisaje.
Si 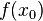 es un mínimo absoluto, entonces para cualquier otro punto
es un mínimo absoluto, entonces para cualquier otro punto  en el dominio de la función, el valor de la función en
en el dominio de la función, el valor de la función en  siempre será mayor o igual que
siempre será mayor o igual que 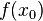 . Se escribe así:
. Se escribe así: 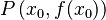 mínimo absoluto de
mínimo absoluto de 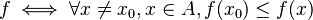 .
.
¿Cómo Encontrar los Extremos de una Función?
Para encontrar los máximos y mínimos de una función, especialmente los locales, usamos una herramienta matemática llamada derivada. La derivada nos dice cómo cambia una función en cada punto.
Cálculo para Funciones Sencillas (Una Variable)
Si tienes una función  que es "suave" (diferenciable), puedes seguir estos pasos:
que es "suave" (diferenciable), puedes seguir estos pasos:
- Paso 1: Calcula la primera derivada de la función, que se escribe como
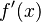 . Esta derivada nos dice la pendiente de la función en cada punto.
. Esta derivada nos dice la pendiente de la función en cada punto. - Paso 2: Calcula la segunda derivada de la función, que se escribe como
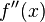 . Esta nos ayuda a saber si un punto es un máximo o un mínimo.
. Esta nos ayuda a saber si un punto es un máximo o un mínimo. - Paso 3: Iguala la primera derivada a cero: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = 0 . Los valores de
 que obtengas al resolver esta ecuación son los "candidatos" a ser máximos o mínimos. Se llaman puntos críticos.
que obtengas al resolver esta ecuación son los "candidatos" a ser máximos o mínimos. Se llaman puntos críticos. - Paso 4: Sustituye cada uno de estos valores de
 en la segunda derivada
en la segunda derivada 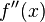 :
:
- Si
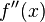 es menor que cero (un número negativo), entonces tienes un máximo en ese punto.
es menor que cero (un número negativo), entonces tienes un máximo en ese punto. - Si
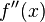 es mayor que cero (un número positivo), entonces tienes un mínimo en ese punto.
es mayor que cero (un número positivo), entonces tienes un mínimo en ese punto. - Si
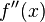 es igual a cero, la prueba no es concluyente. Necesitarías calcular derivadas de orden superior hasta encontrar una que no sea cero. Si esa derivada de orden superior es par y positiva, es un mínimo; si es par y negativa, es un máximo. Si es impar, es un punto de inflexión (donde la curva cambia de concavidad), no un extremo.
es igual a cero, la prueba no es concluyente. Necesitarías calcular derivadas de orden superior hasta encontrar una que no sea cero. Si esa derivada de orden superior es par y positiva, es un mínimo; si es par y negativa, es un máximo. Si es impar, es un punto de inflexión (donde la curva cambia de concavidad), no un extremo.
- Si
Ejemplo Práctico
Vamos a encontrar los extremos de la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = x^3 - 12x^2 + 45x - 30 .
Primero, calculamos las derivadas:
- Primera derivada: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = 3x^2 - 24x + 45
- Segunda derivada: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f''(x) = 6x - 24
- Tercera derivada: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'''(x) = 6
Ahora, buscamos los puntos críticos igualando la primera derivada a cero: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3x^2 - 24x + 45 = 0 Si resolvemos esta ecuación, obtenemos  y
y  .
.
Luego, usamos la segunda derivada para saber si son máximos o mínimos:
- Para
 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f''(3) = 6 \cdot 3 - 24 = 18 - 24 = -6 . Como es negativo (menor que 0), hay un máximo en
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f''(3) = 6 \cdot 3 - 24 = 18 - 24 = -6 . Como es negativo (menor que 0), hay un máximo en  . El valor de la función en ese punto es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(3) = 3^3 - 12(3^2) + 45(3) - 30 = 27 - 108 + 135 - 30 = 24 . Así que el máximo está en el punto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): M(3, 24) .
. El valor de la función en ese punto es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(3) = 3^3 - 12(3^2) + 45(3) - 30 = 27 - 108 + 135 - 30 = 24 . Así que el máximo está en el punto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): M(3, 24) . - Para
 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f''(5) = 6 \cdot 5 - 24 = 30 - 24 = 6 . Como es positivo (mayor que 0), hay un mínimo en
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f''(5) = 6 \cdot 5 - 24 = 30 - 24 = 6 . Como es positivo (mayor que 0), hay un mínimo en  . El valor de la función en ese punto es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(5) = 5^3 - 12(5^2) + 45(5) - 30 = 125 - 300 + 225 - 30 = 20 . Así que el mínimo está en el punto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): m(5, 20) .
. El valor de la función en ese punto es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(5) = 5^3 - 12(5^2) + 45(5) - 30 = 125 - 300 + 225 - 30 = 20 . Así que el mínimo está en el punto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): m(5, 20) .
Finalmente, buscamos puntos de inflexión (donde la curva cambia de forma) igualando la segunda derivada a cero: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6x - 24 = 0 \iff x = 4 . Como la tercera derivada Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'''(4) = 6 no es cero, confirmamos que hay un punto de inflexión en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = 4 . El valor de la función es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(4) = 4^3 - 12(4^2) + 45(4) - 30 = 64 - 192 + 180 - 30 = 22 . El punto de inflexión es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P(4, 22) .
Extremos en Funciones con Varias Variables
Cuando una función depende de más de una variable (por ejemplo, 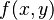 ), el proceso para encontrar los extremos es un poco más complejo. En lugar de una sola derivada, se usan las derivadas parciales y un concepto llamado gradiente.
), el proceso para encontrar los extremos es un poco más complejo. En lugar de una sola derivada, se usan las derivadas parciales y un concepto llamado gradiente.
Por ejemplo, para la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x,y) = x^2 - 2ax + a^2 + y^2 , que se puede escribir como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x,y) = (x - a)^2 + y^2 , el valor más pequeño que puede tomar es 0. Esto ocurre cuando Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x-a=0 (es decir,  ) y
) y  . Así, el mínimo está en
. Así, el mínimo está en 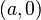 .
.
Para funciones más complicadas, se calculan las derivadas parciales con respecto a cada variable y se igualan a cero. Esto nos da un sistema de ecuaciones que hay que resolver para encontrar los puntos críticos.
Extremos con Condiciones Especiales
A veces, queremos encontrar el máximo o el mínimo de una función, pero con una condición adicional. Por ejemplo, queremos encontrar el punto más alto de una montaña, pero solo si estamos caminando por un sendero específico.
Estos se llaman problemas de extremos condicionados. Se busca un extremo de una función, pero solo en un subconjunto de su dominio. Esto significa que los puntos deben cumplir una condición extra, como una ecuación.
Estos problemas son muy comunes en la vida real, como en la economía o la física, donde se busca optimizar algo bajo ciertas restricciones. Para resolverlos, se usa un método especial llamado el método de los multiplicadores de Lagrange.
Galería de imágenes
Véase también
 En inglés: Maximum and minimum Facts for Kids
En inglés: Maximum and minimum Facts for Kids