Asíntota para niños
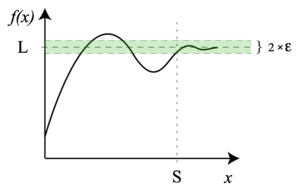
En matemáticas, una asíntota es una línea recta a la que la gráfica de una función se acerca cada vez más, pero sin llegar a tocarla, a medida que se extiende infinitamente. Imagina que son como dos caminos que se acercan mucho, pero nunca se cruzan. Esto significa que la distancia entre la función y la asíntota se hace casi cero a medida que avanzan.
Muchas funciones racionales (que son como fracciones con polinomios arriba y abajo) suelen tener asíntotas.
Contenido
¿Qué son las asíntotas y por qué son importantes?
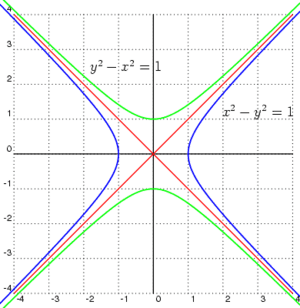
La palabra "asíntota" viene del griego y significa "aquello que no cae" o "aquello que no se encuentra". Esta idea fue usada por un matemático llamado Apolonio de Perga hace mucho tiempo, cuando hablaba de las hipérbolas y las líneas a las que se acercaban sin tocar.
En geometría, las asíntotas nos ayudan a entender cómo se comportan las curvas, especialmente cuando se extienden mucho. Son como guías que nos muestran la dirección que toma una función.
Con el desarrollo del álgebra y el cálculo infinitesimal, la idea de que algo "tiende a infinito" o "tiende a cero" se hizo más precisa usando el concepto de límite matemático. Esto nos permite calcular las asíntotas de forma exacta.
Tipos de asíntotas y cómo se ven
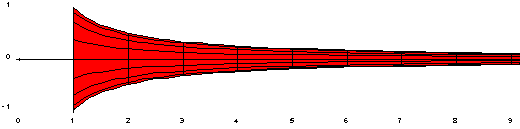
Las asíntotas son muy útiles para dibujar las gráficas de las funciones, porque nos dan una idea de su forma y de cómo se comportan a lo lejos. Aunque las asíntotas son líneas rectas, no forman parte de la función en sí. A menudo se dibujan con líneas punteadas para distinguirlas.
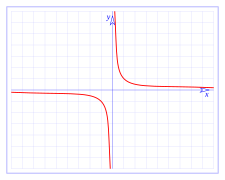
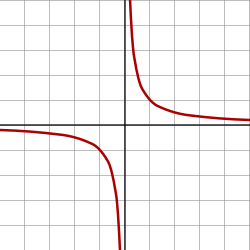
A veces, las asíntotas pueden ser los propios ejes de coordenadas (el eje X o el eje Y).
Existen tres tipos principales de asíntotas:
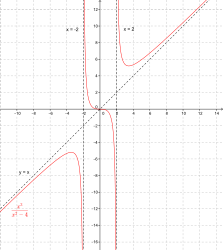
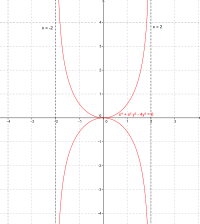
- Asíntotas verticales: Son líneas rectas que van de arriba abajo (perpendiculares al eje X). Su ecuación es del tipo x = un número constante.
- Asíntotas horizontales: Son líneas rectas que van de izquierda a derecha (perpendiculares al eje Y). Su ecuación es del tipo y = un número constante.
- Asíntotas oblicuas: Son líneas rectas inclinadas, que no son ni horizontales ni verticales. Su ecuación es del tipo y = m•x + b, donde 'm' es la pendiente y 'b' es el punto donde cruza el eje Y.
Cómo calcular las asíntotas
En matemáticas, las asíntotas nos ayudan a entender el comportamiento de las funciones en puntos donde no están definidas, como cuando intentamos dividir por cero.
Cálculo de asíntotas usando límites
El concepto de límite matemático es clave para encontrar asíntotas.
- Asíntota vertical: Si al acercarnos a un valor específico de x (por ejemplo, x = a), la función f(x) se va hacia el infinito (positivo o negativo), entonces la línea x = a es una asíntota vertical.
* Ejemplos: la función logaritmo neperiano o la función tangente.
- Asíntota horizontal: Si al hacer que x se vaya hacia el infinito (positivo o negativo), la función f(x) se acerca a un número fijo a, entonces la línea y = a es una asíntota horizontal.
* Ejemplos: la función exponencial o la tangente hiperbólica.
- Asíntota oblicua: Una línea inclinada y = mx + b es una asíntota oblicua si la distancia entre la función y esta línea se hace cero cuando x se va al infinito. Los valores de m y b se calculan con fórmulas especiales que usan límites.
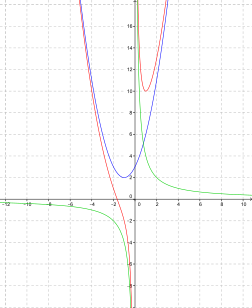
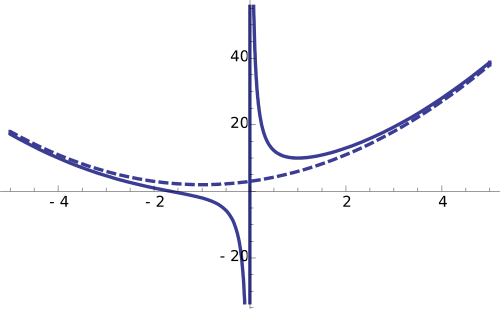
Asíntotas en funciones racionales
Las funciones racionales son funciones que se escriben como una fracción de dos polinomios. Para ellas, las asíntotas son muy importantes para dibujarlas.
Una función racional puede tener varias asíntotas verticales, pero solo una asíntota horizontal o una asíntota oblicua (nunca ambas a la vez).
- Las asíntotas verticales aparecen en los valores de x que hacen que el denominador de la fracción sea cero, siempre y cuando ese valor no haga cero también el numerador.
- Las asíntotas horizontales u oblicuas dependen de los grados de los polinomios del numerador y del denominador:
* Si el grado del polinomio de arriba es menor que el de abajo, hay una asíntota horizontal en y = 0. * Si los grados son iguales, hay una asíntota horizontal en y = a/b, donde 'a' y 'b' son los números que acompañan a las x de mayor grado. * Si el grado del polinomio de arriba es mayor que el de abajo, no hay asíntota horizontal. Si el grado de arriba es exactamente uno más que el de abajo, hay una asíntota oblicua.
Ejemplos:
- La función y = 1/x tiene asíntotas en los propios ejes X e Y.
- Una función como f(x) = (ax + b) / (cx + d) tiene una asíntota vertical en x = -d/c y una horizontal en y = a/c.
Ejemplos de asíntotas en diferentes funciones
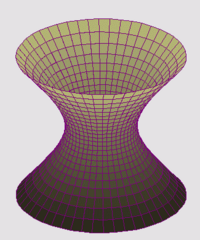
Las asíntotas se encuentran en muchos tipos de funciones, desde las más simples hasta las más complejas, y no solo en dos dimensiones, sino también en superficies tridimensionales. Sirven como "curvas guía" para dibujar otras curvas o funciones.
Funciones trascendentes
Asíntotas verticales cada π.
Curvas polares
Curvas asintóticas
A veces, una curva puede acercarse a otra curva (no solo a una línea recta) a medida que se extiende. A esto se le llama una asíntota curvilínea.
Superficies y estructuras
El concepto de asíntota también se aplica a figuras en tres dimensiones.
Galería de imágenes
Ver también
- Sección cónica
- Infinito
- División por cero
- Derivada
- Clasificación de discontinuidades
- Análisis de algoritmos
- Análisis asintótico
Véase también
 En inglés: Rational function Facts for Kids
En inglés: Rational function Facts for Kids




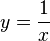
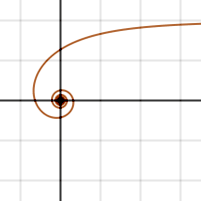

 .
.
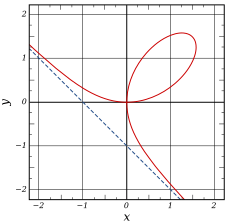
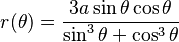
 .
.
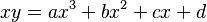 .
.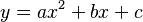 ,
,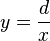
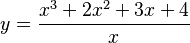 ,
,