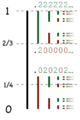0,999… para niños
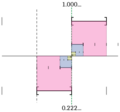
En matemáticas, 0,999... es un número decimal periódico que representa al número 1. Esto significa que, aunque se escriban de forma diferente, los símbolos "0,999..." y "1" son en realidad el mismo número real. Esta idea puede parecer extraña al principio, pero los matemáticos han demostrado que es cierta de varias maneras.
El hecho de que algunos números puedan tener más de una forma de escribirse no es exclusivo del sistema decimal (el que usamos normalmente con base 10). Ocurre en otros sistemas de números y no solo con el número 1. Por ejemplo, el número 2 se puede escribir como 1,999... y el número 28,3287 se puede escribir como 28,3286999... Generalmente, preferimos la forma más sencilla (como 1 o 28,3287), lo que a veces nos hace pensar que es la única forma de representarlos.
La igualdad 0,999... = 1 ha sido aceptada por los matemáticos desde hace mucho tiempo y se enseña en los libros de texto. Sin embargo, a muchos estudiantes les cuesta entenderla o aceptarla al principio. A veces, se convencen porque lo dicen los libros o los profesores, o por algunas explicaciones matemáticas sencillas. Pero otros necesitan una explicación más profunda.
Contenido
¿Por qué 0,999... es igual a 1?
Existen varias formas de demostrar que 0,999... es igual a 1. Algunas son más fáciles de entender que otras.
Usando fracciones
Una forma sencilla de entender por qué 0,999... es igual a 1 es pensando en las fracciones.
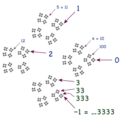
- Sabemos que la fracción 1/3 (un tercio) se puede escribir como el decimal periódico 0,333... (donde el 3 se repite infinitamente).
- Si multiplicamos 1/3 por 3, obtenemos 1 (porque 3 veces un tercio es un entero).
- Si multiplicamos 0,333... por 3, obtenemos 0,999...
- Como 1/3 multiplicado por 3 es igual a 1, y 0,333... multiplicado por 3 es igual a 0,999..., entonces 0,999... debe ser igual a 1.
Aquí te lo mostramos con números: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \frac{1}{3} & = 0,333\dots \\ 3 \times \frac{1}{3} & = 3 \times 0,333\dots \\ 1 & = 0,999\dots \end{align}
Multiplicando por 10
Otra forma de demostrarlo es usando un poco de álgebra. 1. Imagina que el número 0,999... es una cantidad que llamaremos x. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = 0,999\ldots 2. Si multiplicamos x por 10, el punto decimal se mueve un lugar a la derecha. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10 x = 9,999\ldots 3. Ahora, restamos el valor original de x (0,999...) de 10x (9,999...). Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10 x - x = 9,999\ldots - 0,999\ldots 4. Al hacer la resta, todos los 9s después del punto decimal se cancelan, y nos queda: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 9 x = 9 5. Finalmente, si dividimos ambos lados por 9, obtenemos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = 1 Esto significa que x, que era 0,999..., es igual a 1.
Usando series infinitas
En matemáticas más avanzadas, los números decimales infinitos se pueden entender como la suma de una serie infinita. El número 0,999... se puede escribir como: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0,999\ldots = \frac{9}{10} + \frac{9}{100} + \frac{9}{1000} + \ldots Esto es una serie geométrica donde cada término es 1/10 del anterior. La suma de una serie geométrica infinita con una razón menor que 1 se puede calcular con una fórmula. Aplicando esa fórmula, la suma de 0,999... resulta ser exactamente 1.
Usando límites
También podemos pensar en 0,999... como el límite de una sucesión de números que se acercan cada vez más a 1:
- 0,9
- 0,99
- 0,999
- 0,9999
...y así sucesivamente.
A medida que añadimos más nueves, el número se acerca más y más a 1. El límite de esta sucesión es 1. Esto significa que 0,999... no es "casi 1", sino que es exactamente 1.
¿Por qué a veces es difícil de creer?
Muchos estudiantes, y a veces incluso adultos, tienen dudas sobre la igualdad 0,999... = 1. Esto puede deberse a varias razones:
- Apariencia diferente: Los números 0,999... y 1 se ven muy distintos, lo que hace difícil creer que sean lo mismo.
- Pensar en un "último 9": Algunas personas creen que en 0,999... debe haber un "último 9" al final de la secuencia infinita, lo cual no es posible en un número infinito.
- Confusión con el concepto de límite: A veces, se piensa que un límite es un proceso que nunca termina o que nunca "alcanza" su valor final, en lugar de ser el valor exacto al que se llega.
Estas ideas son comunes, pero en el sistema de números reales que usamos en matemáticas, 0,999... y 1 son el mismo número.
0,999... en la cultura popular
La discusión sobre 0,999... = 1 no se limita a las aulas de matemáticas. Con la llegada de Internet, este tema se ha vuelto un debate popular en foros y grupos de discusión, incluso en aquellos que no tienen mucho que ver con las matemáticas. Es una de las preguntas frecuentes en algunos sitios web de ciencia y matemáticas.
Incluso algunas empresas de videojuegos han bromeado sobre el tema. Por ejemplo, en 2004, la compañía Blizzard Entertainment (creadora de juegos populares) publicó un comunicado el Día de los Inocentes (1 de abril) afirmando que 0,999... es definitivamente igual a 1, y ofrecieron dos pruebas basadas en límites y multiplicación por 10.
Este concepto también ha aparecido en el folclore matemático, como en el siguiente chiste: Pregunta: ¿Cuántos matemáticos se necesitan para cambiar un foco? Respuesta: 0,999999...
Generalizaciones
La idea de que 0,999... = 1 se puede aplicar a otros números y sistemas.
- Otros números: Cualquier número decimal que termina (como 0,25) también tiene una representación con infinitos nueves (como 0,24999...). Ambos son el mismo número.
- Otras bases: En otros sistemas de numeración, como el sistema binario (base 2) o el sistema ternario (base 3), también ocurre algo similar. Por ejemplo, en base 2, 0,111... es igual a 1.
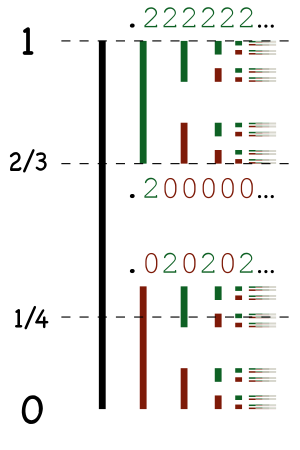
En el análisis real, el caso de 0,222... = 1 en base 3 es importante para entender un fractal llamado el conjunto de Cantor. Este conjunto se construye quitando la parte central de un segmento de línea una y otra vez. Un punto está en el conjunto de Cantor si se puede representar en base 3 usando solo los dígitos 0 y 2.
Galería de imágenes
-
Posiciones de 1/4, 2/3, y 1 en el conjunto de Cantor
Véase también
 En inglés: 0.999... Facts for Kids
En inglés: 0.999... Facts for Kids
- Representación decimal
- Número periódico
- Uno
- Infinito
- Serie matemática
- Serie geométrica
- Límite matemático


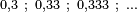 que converge a 1.
que converge a 1.