Función periódica para niños
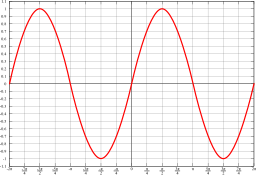
Una función es periódica si su gráfica se repite una y otra vez a intervalos regulares. Imagina un patrón que se repite: eso es lo que hace una función periódica. El tiempo o la distancia que tarda en repetirse se llama periodo. El periodo más corto que hace que la función se repita se llama periodo fundamental.
Las funciones que se usan en matemáticas para describir ondas, como las funciones seno y coseno, son ejemplos perfectos de funciones periódicas.
En el mundo de la física, las ondas periódicas son aquellas que se repiten con el tiempo. Piensa en las olas del mar que llegan a la orilla una tras otra, o en el sonido de una nota musical que se mantiene constante.
En una onda periódica, si miras su forma en un momento dado, esa misma forma se repetirá exactamente después de un tiempo llamado periodo (representado como Tp). Este periodo está relacionado con la frecuencia (F), que es cuántas veces se repite la onda en un segundo. La fórmula es Tp = 1/F.
Todas las ondas periódicas pueden describirse con fórmulas matemáticas, lo que las hace "deterministas", es decir, predecibles.
Contenido
¿Qué son las ondas periódicas?
La forma más sencilla de onda periódica es la onda sinusoidal, que parece una "S" suave que se repite. Se puede describir con una fórmula que usa tres cosas importantes:
- Amplitud (A): Es la altura máxima de la onda desde su punto central. Imagina cuán alta es una ola.
- Frecuencia (Ω o F): Es la rapidez con la que la onda se repite. Se mide en radianes por segundo (rad/s) o en hercios (Hz). Un hercio significa que la onda se repite una vez por segundo.
- Fase (θ): Indica dónde empieza la onda en su ciclo.
Ondas complejas y el trabajo de Fourier
No todas las ondas periódicas son tan simples como una onda sinusoidal. Algunas tienen formas más complicadas. Pero un matemático llamado Jean-Baptiste Joseph Fourier descubrió algo asombroso: ¡cualquier onda periódica compleja puede formarse sumando muchas ondas sinusoidales simples!
Imagina que tienes un montón de piezas de LEGO de diferentes tamaños y colores. Puedes usarlas para construir una casa simple o una nave espacial muy elaborada. De manera similar, las ondas sinusoidales son como las piezas de LEGO de las ondas.
- Análisis de Fourier: Es el proceso de "descomponer" una onda compleja para ver qué ondas sinusoidales simples la forman y cuán importantes son.
- Síntesis de Fourier: Es el proceso contrario, donde "construyes" una onda compleja sumando diferentes ondas sinusoidales.
En la práctica, especialmente en las telecomunicaciones, las ondas no tienen un número infinito de estas ondas simples (llamadas armónicos). Siempre hay un número limitado. La onda sinusoidal simple es el caso más básico, con un solo armónico.
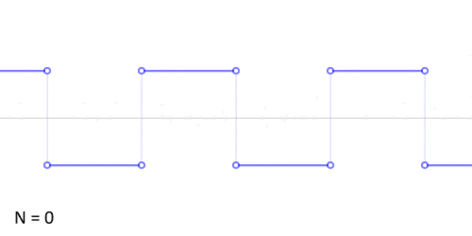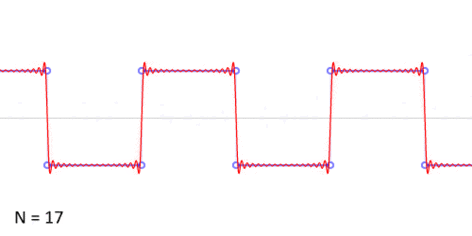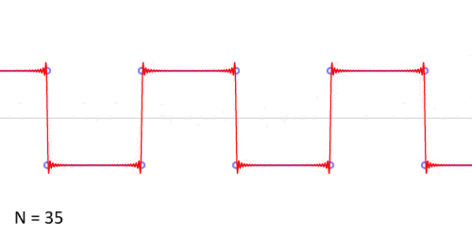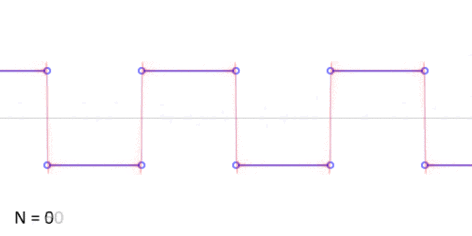
Algunas ondas, como las ondas cuadradas (que suben y bajan de golpe, como un interruptor de luz) o las ondas triangulares (que suben y bajan en línea recta), necesitan muchos armónicos para formarse. Aunque en la vida real no podemos crear ondas con infinitos armónicos, sus aproximaciones (con un número limitado) son muy útiles.
Este descubrimiento de Fourier es muy importante en la Teoría de la Información. Por ejemplo, ayuda a entender cómo podemos tomar "muestras" de una onda (como cuando grabas un sonido) y luego reconstruirla perfectamente, siempre y cuando tomemos suficientes muestras.
Características de las ondas periódicas
Valor medio
El valor medio de una onda periódica es como calcular el promedio de todos sus valores durante un periodo completo. A menudo, el valor medio de una onda periódica es cero. Esto significa que la onda pasa tanto tiempo por encima como por debajo de su punto central. En electrónica, un valor medio diferente de cero indica que hay una parte de corriente continua en la señal.
Valor eficaz (RMS)
El valor eficaz (también conocido como RMS, por sus siglas en inglés) es una forma de medir la "potencia" o "energía" de una onda periódica. Es especialmente útil en física para calcular la energía que transportan las ondas, como la electricidad.
Para diferentes tipos de ondas, el valor eficaz se calcula de manera distinta en relación con su valor máximo (el punto más alto de la onda):
- Onda sinusoidal: El valor eficaz es aproximadamente 0.707 veces el valor máximo.
- Onda cuadrada: El valor eficaz es igual al valor máximo.
- Onda triangular: El valor eficaz es aproximadamente 0.577 veces el valor máximo.
Factor de pico o cresta
Este factor nos dice qué tan "puntiaguda" es una onda. Se calcula dividiendo el valor máximo de la onda entre su valor eficaz.
- Onda sinusoidal: Factor de pico es aproximadamente 1.414.
- Onda cuadrada: Factor de pico es 1.
- Onda triangular: Factor de pico es aproximadamente 1.732.
Ejemplos de funciones periódicas
En nuestra vida diaria, vemos muchos ejemplos de cosas que se repiten periódicamente:
- El movimiento de las manecillas de un reloj.
- Las fases de la luna (luna nueva, cuarto creciente, luna llena, etc.).
- Las estaciones del año (primavera, verano, otoño, invierno).
- El latido de tu corazón.
Un movimiento periódico es cuando la posición de algo se repite siguiendo funciones periódicas, todas con el mismo periodo.
Si una función es periódica con un periodo P, significa que si miras la función en un punto x, tendrá el mismo valor en x + P, x + 2P, x + 3P, y así sucesivamente.
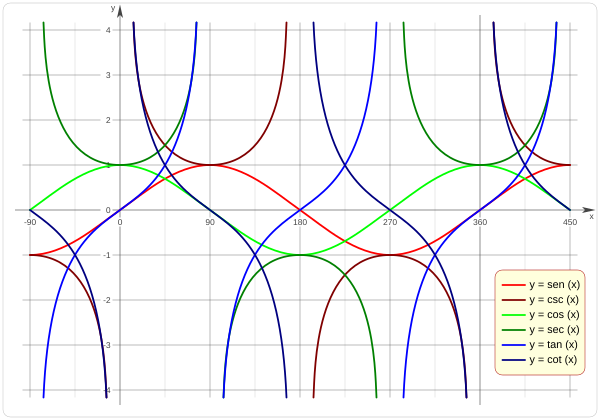
Las funciones trigonométricas como el seno y el coseno son periódicas con un periodo de 360 grados (o 2π radianes). La función tangente tiene un periodo más corto, de 180 grados (o π radianes).
Galería de imágenes
-
Un ejemplo de una función periódica con periodo P.
Véase también
 En inglés: Periodic function Facts for Kids
En inglés: Periodic function Facts for Kids
- Teorema de muestreo de Nyquist-Shannon
- Oscilador armónico
- Serie de Fourier