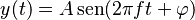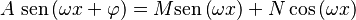Sinusoide para niños
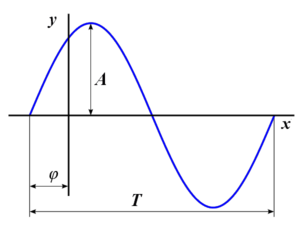
En matemática se denomina sinusoide o senoide a la curva que representa gráficamente la función seno. Es una curva que describe un movimiento de onda que se repite de forma suave.
Su forma más básica, que depende del tiempo (t), se expresa así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(t) = A\sen(\omega t + \varphi)
La sinusoide es muy importante en física. Esto se debe a un principio llamado teorema de Fourier. Este teorema dice que cualquier onda, sin importar su forma, puede formarse sumando muchas ondas sinusoidales con diferentes tamaños y longitudes. Por eso, esta función se usa para representar tanto las ondas de sonido como las de la corriente alterna (la electricidad que usamos en casa).
Contenido
¿Qué es una onda sinusoidal pura?
Una onda sinusoidal representa una sola frecuencia sin otros sonidos añadidos, llamados armónicos. En el mundo del sonido, se considera un tono puro. Si sumamos ondas sinusoidales de diferentes frecuencias, obtenemos una forma de onda distinta. La presencia de armónicos más altos, además de la frecuencia fundamental (el tono principal), cambia el timbre. Por eso, la misma nota musical suena diferente si la toca una guitarra o un piano.
Características principales de una sinusoide
La sinusoide se describe con estas expresiones matemáticas:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(t) = A\ {\rm{sen}}\left (\omega t + \varphi \right )
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(t) = A\ {\rm{sen}} \left (\frac {2\pi }{T}t + \varphi \right )
Aquí, cada letra tiene un significado:
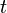 es el valor que cambia, normalmente el tiempo en segundos.
es el valor que cambia, normalmente el tiempo en segundos. es la amplitud, que indica qué tan grande es la oscilación.
es la amplitud, que indica qué tan grande es la oscilación. es la frecuencia, que dice cuántas veces se repite la onda en un segundo.
es la frecuencia, que dice cuántas veces se repite la onda en un segundo.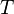 es el período, que es el tiempo que tarda la onda en completar un ciclo. Se calcula como
es el período, que es el tiempo que tarda la onda en completar un ciclo. Se calcula como 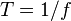 .
.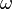 es la velocidad angular, relacionada con la frecuencia por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \omega = 2\pi f .
es la velocidad angular, relacionada con la frecuencia por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \omega = 2\pi f .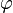 es la fase inicial, que nos dice dónde empieza la onda en el tiempo.
es la fase inicial, que nos dice dónde empieza la onda en el tiempo.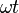 +
+ 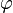 es la fase de oscilación, que describe el punto actual de la onda en su ciclo.
es la fase de oscilación, que describe el punto actual de la onda en su ciclo.
¿Qué es el período (T) en una sinusoide?
El período es el tiempo más corto que necesita una onda para completar un ciclo completo y empezar a repetirse. Imagina que es el tiempo que tarda una ola en el mar en pasar por un punto y que la siguiente ola idéntica llegue a ese mismo punto.
En las gráficas de las funciones seno y coseno, el período es 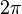 .
.
¿Qué es la amplitud (A) en una sinusoide?
La amplitud es la altura máxima que alcanza la curva de la onda desde su punto central (el eje x). Cuanto mayor sea la amplitud, más "fuerte" o "intensa" es la onda. Por ejemplo, en el sonido, una mayor amplitud significa un sonido más fuerte.
¿Qué es la fase inicial (φ) en una sinusoide?
La fase inicial nos indica el punto de partida de la onda. Es como si moviéramos la onda hacia la izquierda o la derecha en la gráfica.
- Si dos ondas sinusoidales tienen la misma frecuencia y la misma fase, decimos que están en fase. Esto significa que sus picos y valles coinciden.
- Si dos ondas sinusoidales tienen la misma frecuencia pero diferente fase, decimos que están desfasadas. Una onda puede estar "adelantada" o "atrasada" respecto a la otra.
No tiene sentido comparar la fase de dos ondas con frecuencias diferentes, porque sus picos y valles no coincidirán de forma constante.
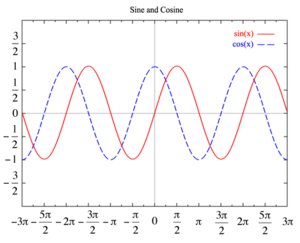
Sinusoide y cosinusoide: ¿Son lo mismo?
Las funciones seno y coseno son muy parecidas. De hecho, la función coseno es una sinusoide que está "desplazada" o "desfasada" un poco.
Podemos transformar una combinación de seno y coseno en una sola sinusoide, y viceversa. Esto se debe a que:
donde:
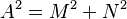
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varphi = \arctan \frac {N}{M}
Si M es menor que 0, se considera Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varphi = \arctan \frac {N}{M} + \pi .
Un caso especial es cuando Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varphi = \pi/2 :
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): { {\rm{sen}} \left (\omega x + \pi/2 \right ) = \rm{cos}} \left (\omega x \right )
Esto significa que la función seno y la función coseno son la misma sinusoide, pero la coseno está desplazada 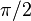 radianes respecto a la seno.
radianes respecto a la seno.
Ondas que cambian con la posición y el tiempo
Algunas ondas existen tanto en el espacio (posición) como en el tiempo. Estas ondas tienen:
- Una variable espacial
 que indica la posición en la dirección en la que se mueve la onda.
que indica la posición en la dirección en la que se mueve la onda. - Un número de onda angular
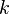 , que relaciona la velocidad angular
, que relaciona la velocidad angular 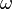 con la velocidad a la que se propaga la onda (
con la velocidad a la que se propaga la onda (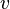 ):
):
- El número de onda se relaciona con la velocidad angular así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\textstyle k {=} \frac{\omega}{v} {=} \frac{2 \pi f}{v} {=} \frac{2 \pi}{\lambda}} , donde
 (lambda) es la longitud de onda (la distancia entre dos picos de la onda).
(lambda) es la longitud de onda (la distancia entre dos picos de la onda).
- El número de onda se relaciona con la velocidad angular así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\textstyle k {=} \frac{\omega}{v} {=} \frac{2 \pi f}{v} {=} \frac{2 \pi}{\lambda}} , donde
Dependiendo de hacia dónde se muevan, estas ondas pueden tener la siguiente forma (usando la función seno como ejemplo):
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(x, t) = A\sen(kx - \omega t + \varphi) , si la onda se mueve hacia la derecha.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y(x, t) = A\sen(kx + \omega t + \varphi) , si la onda se mueve hacia la izquierda.
¿Qué son las ondas estacionarias?
Cuando dos ondas con la misma amplitud y frecuencia viajan en direcciones opuestas y se encuentran (se superponen), pueden formar un patrón llamado onda estacionaria. Estas ondas parecen no moverse, aunque en realidad son el resultado de dos ondas que sí se mueven.
Un ejemplo común es una cuerda de guitarra. Cuando la pulsas, las ondas viajan por la cuerda y se reflejan en los extremos fijos. Las frecuencias que hacen que la cuerda vibre de forma estable son las únicas que producen ondas estacionarias. Esto ocurre solo para longitudes de onda que son el doble de la longitud de la cuerda (que es la frecuencia fundamental) o divisiones exactas de esta (que son los armónicos superiores).
Ondas en más de una dimensión
Las ecuaciones anteriores describen el movimiento de una onda en una sola línea (una dimensión). Por ejemplo, el valor de una onda a lo largo de un cable.
En dos o tres dimensiones, la misma ecuación puede describir una onda plana que se mueve. En este caso, la posición  y el número de onda angular
y el número de onda angular 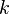 se consideran vectores (cantidades con dirección y magnitud). Para ondas más complejas, como la altura de una ola en un estanque después de que cae una piedra, se necesitan ecuaciones más elaboradas.
se consideran vectores (cantidades con dirección y magnitud). Para ondas más complejas, como la altura de una ola en un estanque después de que cae una piedra, se necesitan ecuaciones más elaboradas.
Otros temas relacionados
- Cresta (ola)
- Transformada de Fourier
- Movimiento armónico simple
- Onda (física)
- Ecuación de onda
- Interferencia
Véase también
 En inglés: Sine wave Facts for Kids
En inglés: Sine wave Facts for Kids