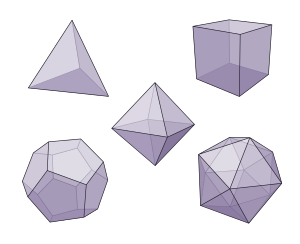
Sólidos platónicos para niños

Los cinco sólidos platónicos.

Los sólidos platónicos son formas geométricas especiales en 3D. Se les llama así porque el filósofo griego Platón los estudió hace mucho tiempo. También se les conoce como poliedros regulares convexos o cuerpos cósmicos.

Un sólido platónico tiene estas características:

• Todas sus caras son polígonos regulares (como triángulos equiláteros, cuadrados o pentágonos regulares) y son exactamente iguales entre sí.
• En cada esquina (vértice) del sólido, se unen el mismo número de caras y de bordes (aristas).
• Todos sus ángulos son iguales.

El matemático Teeteto, que vivió en la misma época que Platón, ayudó a desarrollar la teoría sobre estos sólidos. Además, el matemático Leonhard Euler descubrió una fórmula importante para ellos: V + C = A + 2. Aquí, V es el número de vértices, C es el número de caras y A es el número de aristas.

Solo existen cinco sólidos platónicos: el tetraedro, el cubo (también llamado hexaedro regular), el octaedro, el dodecaedro y el icosaedro. No es posible crear ningún otro sólido que cumpla todas estas propiedades.

Historia de los Sólidos Platónicos

Se sabe que estas formas eran conocidas desde hace mucho tiempo. Se han encontrado bolas de piedra tallada con estas formas en Escocia, que datan de hace unos 4000 años.

Los antiguos griegos estudiaron mucho los sólidos platónicos. Algunos creen que Pitágoras los descubrió, pero otras pruebas sugieren que él solo conocía el tetraedro, el cubo y el dodecaedro. Se piensa que Teeteto fue quien descubrió el octaedro y el icosaedro. Teeteto también fue el primero en demostrar matemáticamente que solo existen estos cinco sólidos.

Platón, en uno de sus diálogos llamado Timeo, relacionó cada sólido platónico con un elemento:

• El tetraedro con el fuego.
• El octaedro con el aire.
• El icosaedro con el agua.
• El cubo con la tierra.

Platón pensó que el quinto sólido, el dodecaedro, fue usado por Dios para representar el universo. Más tarde, el matemático Euclides describió detalladamente los sólidos platónicos en su famoso libro Los elementos.

¿Por qué solo hay cinco Sólidos Platónicos?

Es una pregunta interesante, ¿verdad? Aquí te explicamos de forma sencilla por qué no puede haber más de cinco.

Demostración Geométrica Sencilla

Imagina que estás construyendo un sólido 3D. Para que sea un sólido platónico, debe cumplir algunas reglas:

1. Cada esquina (vértice) del sólido debe tener al menos tres caras que se unan en ella.
2. Cuando las caras se unen en un vértice, la suma de los ángulos de esas caras alrededor del vértice debe ser menor de 360 grados. Si fuera 360 grados o más, las caras se aplanarían o se superpondrían, y no formarían un sólido.

Ahora, pensemos en los polígonos regulares que pueden ser las caras:

• Los polígonos con seis o más lados (como hexágonos) tienen ángulos interiores de 120 grados o más. Si juntas tres o más de estos, la suma de los ángulos sería 360 grados o más. Por eso, las caras de un sólido platónico solo pueden ser triángulos, cuadrados o pentágonos regulares.

Veamos cada caso:

• Caras triangulares: Un triángulo equilátero tiene ángulos de 60 grados.

* Si juntas 3 triángulos: 3 x 60° = 180°. Esto forma un tetraedro. * Si juntas 4 triángulos: 4 x 60° = 240°. Esto forma un octaedro. * Si juntas 5 triángulos: 5 x 60° = 300°. Esto forma un icosaedro. * Si juntas 6 triángulos: 6 x 60° = 360°. Esto ya no forma un sólido.

• Caras cuadradas: Un cuadrado tiene ángulos de 90 grados.

* Si juntas 3 cuadrados: 3 x 90° = 270°. Esto forma un cubo. * Si juntas 4 cuadrados: 4 x 90° = 360°. Esto ya no forma un sólido.

• Caras pentagonales: Un pentágono regular tiene ángulos de 108 grados.

* Si juntas 3 pentágonos: 3 x 108° = 324°. Esto forma un dodecaedro. * Si juntas 4 pentágonos: 4 x 108° = 432°. Esto ya no forma un sólido.

Como puedes ver, al analizar todas las posibilidades, solo podemos formar cinco sólidos platónicos.

Demostración con la Fórmula de Euler

También podemos usar una fórmula matemática para demostrarlo. La fórmula de Euler para poliedros dice que: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V - A + C = 2 Donde V es el número de vértices, A el número de aristas y C el número de caras.

En un sólido platónico, todas las caras son el mismo tipo de polígono regular (con 'p' lados) y en cada vértice se unen el mismo número de aristas (con 'q' aristas). Usando estas ideas y la fórmula de Euler, se llega a una condición matemática que solo se cumple para cinco combinaciones de 'p' y 'q'. Estas cinco combinaciones corresponden a los cinco sólidos platónicos:

• (3,3) para el tetraedro (caras de 3 lados, 3 aristas por vértice)
• (3,4) para el octaedro (caras de 3 lados, 4 aristas por vértice)
• (3,5) para el icosaedro (caras de 3 lados, 5 aristas por vértice)
• (4,3) para el cubo (caras de 4 lados, 3 aristas por vértice)
• (5,3) para el dodecaedro (caras de 5 lados, 3 aristas por vértice)

Características de los Sólidos Platónicos

Regularidad y Simetría

Los sólidos platónicos son muy especiales por su perfección y equilibrio:

• Sus caras son polígonos regulares idénticos.
• En cada vértice se unen el mismo número de caras y aristas.
• Todas sus aristas tienen la misma longitud.
• Los ángulos entre sus caras (llamados ángulos diedros) son todos iguales.
• Son figuras muy simétricas. Tienen un punto central desde el que todas las caras, vértices y aristas están a la misma distancia.
• También tienen ejes de simetría (líneas imaginarias alrededor de las cuales puedes girarlos y se ven igual) y planos de simetría (planos imaginarios que los dividen en dos partes idénticas como un espejo).

Gracias a esta simetría, se pueden dibujar tres esferas alrededor de cada sólido platónico, todas con el mismo centro que el sólido:

• Una esfera que toca el centro de todas sus caras (esfera inscrita).
• Una esfera que toca el centro de todas sus aristas.
• Una esfera que pasa por todos sus vértices (esfera circunscrita).

Poliedros Conjugados

Si tomas un sólido platónico y usas el centro de cada una de sus caras como los nuevos vértices de otra figura, obtendrás otro sólido platónico. A este nuevo sólido se le llama el conjugado o dual del primero.

• El conjugado de un dodecaedro es un icosaedro, y viceversa.
• El conjugado de un cubo es un octaedro, y viceversa.
• El conjugado de un tetraedro es otro tetraedro (se dice que es "autoconjugado").

Tabla Comparativa de los Sólidos Platónicos

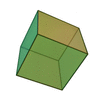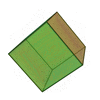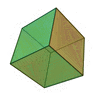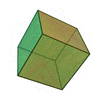
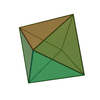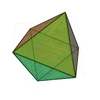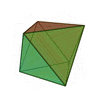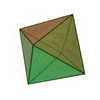
Sólidos Platónicos	Tetraedro	Hexaedro o Cubo	Octaedro	Dodecaedro	Icosaedro
Animación
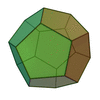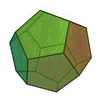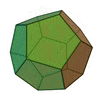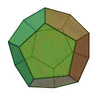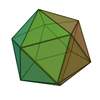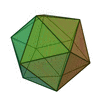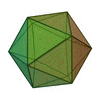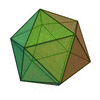Desarrollo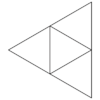
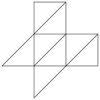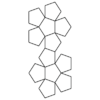Número de caras	4	6	8	12	20
Polígonos que forman las caras	Triángulos Equiláteros	Cuadrados	Triángulos Equiláteros	Pentágonos Regulares	Triángulos Equiláteros
Número de aristas	6	12	12	30	30
Número de vértices	4	8	6	20	12
Caras concurrentes en cada vértice	3	3	4	3	5
Vértices contenidos en cada cara	3	4	3	5	3
Poliedro dual	Tetraedro (autoconjugado)	Octaedro	Hexaedro, Cubo	Icosaedro	Dodecaedro
Ángulo diedro	70.53°	90°	109.47°	116.56°	138.19°

Sólidos Platónicos en la Naturaleza

Aunque parezcan figuras abstractas de matemáticas, los sólidos platónicos aparecen en la naturaleza. Por ejemplo, la estructura básica de algunos virus, como el VIH, tiene la forma de un icosaedro regular.

Galería de imágenes

• 

  Representación de los sólidos platónicos como grafos planos.

Véase también

En inglés: Platonic solid Facts for Kids