Eneadecágono para niños
Datos para niños Eneadecágono |
||
|---|---|---|
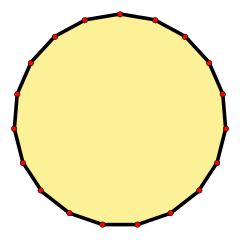 Un eneadecágono rjegular
|
||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 19 | |
| Vértices | 19 | |
| Grupo de simetría | 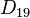 , orden 2x19 , orden 2x19 |
|
| Símbolo de Schläfli | {19} (eneadecágono regular) | |
| Diagrama de Coxeter-Dynkin | ||
| Polígono dual | Autodual | |
| Área | 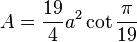 (lado  ) ) |
|
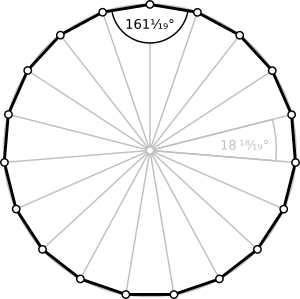
| Ángulo interior | 161+1/19° ≈ 161,0526315789 | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un eneadecágono o nonadecágono es una figura plana con 19 lados rectos y 19 esquinas o vértices. Es un tipo de polígono.
Contenido
¿Qué es un Eneadecágono?
Un eneadecágono es un polígono que tiene exactamente 19 lados. Cada uno de estos lados se une en un punto llamado vértice. Por lo tanto, un eneadecágono también tiene 19 vértices.
¿Cuántas diagonales tiene un eneadecágono?
Una diagonal es una línea que conecta dos vértices de un polígono que no están unidos por un lado. Para saber cuántas diagonales tiene un eneadecágono, podemos usar una fórmula especial.
La fórmula para calcular el número de diagonales de cualquier polígono es: 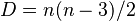 Donde 'n' es el número de lados del polígono. Como un eneadecágono tiene 19 lados (n=19), el cálculo sería:
Donde 'n' es el número de lados del polígono. Como un eneadecágono tiene 19 lados (n=19), el cálculo sería: 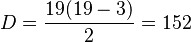 Así, un eneadecágono tiene 152 diagonales.
Así, un eneadecágono tiene 152 diagonales.
¿Cuál es la suma de sus ángulos internos?
La suma de todos los ángulos internos de cualquier eneadecágono siempre es la misma. Esta suma es de 3060 grados.
Eneadecágono Regular
Un eneadecágono regular es un tipo especial de eneadecágono. En esta figura, todos sus 19 lados tienen la misma longitud. Además, todos sus ángulos internos son exactamente iguales.
Medida de los ángulos
Cada ángulo interno de un eneadecágono regular mide aproximadamente 161.05 grados. Esto es un poco más de un ángulo recto (90 grados). Cada ángulo externo de un eneadecágono regular mide aproximadamente 18.95 grados.
¿Cómo calcular el perímetro?
El perímetro es la medida del contorno de una figura. Para un eneadecágono regular, puedes calcular su perímetro P multiplicando la longitud de uno de sus lados (llamémosla t) por 19, que es el número total de lados. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P = 19 \cdot t
¿Cómo calcular el área?
El área es la medida de la superficie que cubre la figura. Para un eneadecágono regular, puedes calcular su área A usando la longitud de su lado t con esta fórmula: 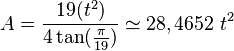 Aquí,
Aquí,  es la constante pi (aproximadamente 3.14159) y
es la constante pi (aproximadamente 3.14159) y 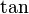 es la función tangente, que se usa en trigonometría.
es la función tangente, que se usa en trigonometría.
También puedes calcular el área si conoces la longitud de la apotema a. La apotema es la distancia desde el centro del polígono hasta el punto medio de uno de sus lados. La fórmula sería:
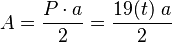
Construcción de un Eneadecágono
Dibujar un eneadecágono regular usando solo una regla y compás es muy difícil, de hecho, no es posible de forma perfecta. Esto se debe a que el número 19 es un tipo especial de número primo llamado número primo de Pierpont, pero no es un número de Fermat.
Sin embargo, existen otros métodos para dibujarlo con mucha precisión. Por ejemplo, se puede usar una técnica llamada "neusis" o herramientas especiales que ayudan a dividir ángulos en tres partes iguales.
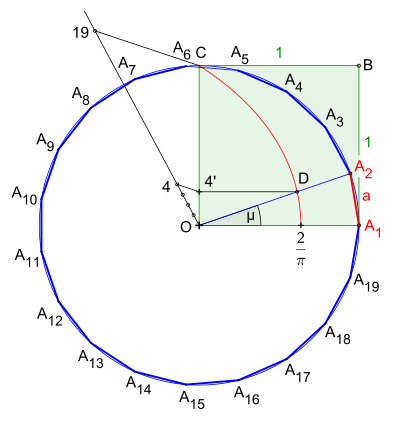
Aquí puedes ver una animación de cómo se puede construir un eneadecágono de forma aproximada.
Incluso con métodos de construcción muy precisos, como los que se usan en programas de computadora, puede haber un error muy pequeño. Por ejemplo, si dibujaras un eneadecágono con un radio de 1000 millones de kilómetros, el error en la longitud de un lado sería de solo 0.21 milímetros. ¡Es un error casi imperceptible!
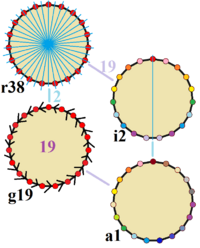
Simetría del Eneadecágono
Un eneadecágono regular tiene una simetría especial. Esto significa que si lo giras o lo volteas de ciertas maneras, se verá exactamente igual. Esta simetría se llama simetría diedral Dih19.
Como 19 es un número primo, el eneadecágono tiene varias formas de simetría. Los matemáticos clasifican estas simetrías para entender mejor las formas de las figuras.
Polígonos relacionados: Eneadecagramas
Un eneadecagrama es una estrella (figura geométrica) que tiene 19 puntas. Se forman conectando los vértices de un eneadecágono regular de diferentes maneras.
Existen ocho tipos de eneadecagramas regulares, cada uno con una forma única. Como 19 es un número primo, todos estos eneadecagramas son estrellas "puras" y no combinaciones de otras figuras.
| Imagen |  {19/2} |
 {19/3} |
 {19/4} |
 {19/5} |
|---|---|---|---|---|
| Ángulo interior | ≈142.105° | ≈123.158° | ≈104.211° | ≈85.2632° |
| Imagen |  {19/6} |
 {19/7} |
 {19/8} |
 {19/9} |
| Ángulo interior | ≈66.3158° | ≈47.3684° | ≈28.4211° | ≈9.47368° |
Polígonos de Petrie
El eneadecágono regular también aparece en la geometría de dimensiones más altas. Es lo que se conoce como un polígono de Petrie para un símplex de 18 dimensiones. Esto significa que si proyectas esta figura de alta dimensión de una manera especial, verías un eneadecágono.
 símplex (18D) |
Véase también
 En inglés: Enneadecagon Facts for Kids
En inglés: Enneadecagon Facts for Kids