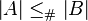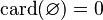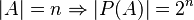Número cardinal para niños
Un número cardinal nos dice cuántos elementos tiene un conjunto. Piensa en un conjunto como una colección de cosas. Por ejemplo, si tienes un conjunto de tres manzanas, el número cardinal de ese conjunto es 3. Este concepto es muy útil porque nos permite contar elementos, ya sean pocos o muchísimos, ¡incluso si son infinitos!
Los números cardinales son una forma más general de entender los números naturales (1, 2, 3, etc.). Nos ayudan a comparar el tamaño de diferentes colecciones, incluso las que tienen una cantidad infinita de elementos.
Para representar el número cardinal de un conjunto llamado 
, usamos símbolos como 
, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mbox{n}(A) , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mbox{card}(A) o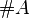 
. Por ejemplo, si el conjunto tiene tres elementos, escribimos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A| = 3 .
Contenido
Historia de los números cardinales
¿Quién inventó el concepto de cardinalidad?
El matemático Georg Cantor desarrolló la idea de los números cardinales en 1874. Él extendió este concepto a los conjuntos infinitos. Para los conjuntos finitos (los que tienen un número limitado de elementos), la idea de contar es bastante sencilla.
Cantor usó la idea de "correspondencia uno a uno" para definir la cardinalidad. Esto significa que si puedes emparejar cada elemento de un conjunto con un elemento de otro conjunto sin que sobre ni falte ninguno, entonces ambos conjuntos tienen el mismo número de elementos.
Por ejemplo, si tienes un conjunto de 3 lápices y un conjunto de 3 gomas, puedes emparejar cada lápiz con una goma. Esto demuestra que ambos conjuntos tienen la misma cardinalidad: 3.
Comparando conjuntos infinitos
Esta idea de correspondencia uno a uno le permitió a Cantor comparar el tamaño de los conjuntos infinitos. Algunos conjuntos infinitos pueden emparejarse uno a uno con el conjunto de los números naturales (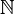
= {1, 2, 3, ...}).
Sin embargo, en 1891, Cantor demostró algo sorprendente. Probó que existen conjuntos infinitos que son "más grandes" que el conjunto de los números naturales. Lo hizo con un método muy inteligente llamado el argumento diagonal.
Cantor llamó al cardinal del conjunto de los números naturales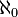 
(se lee "Álef cero"). También demostró que muchos conjuntos infinitos formados por números naturales (como los números pares) tienen la misma cardinalidad 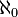. Esto es porque se puede establecer una correspondencia uno a uno con los números naturales.
Propiedades de los números cardinales
Los conjuntos se pueden agrupar según su cardinalidad. Dos conjuntos tienen la misma cardinalidad si puedes encontrar una forma de emparejar sus elementos uno a uno. Si dos conjuntos y 
tienen la misma cardinalidad, lo escribimos así:
o
También podemos comparar el tamaño de los conjuntos. Si puedes emparejar cada elemento del conjunto con un elemento del conjunto sin que te sobren elementos en , entonces el conjunto es "más pequeño o igual" que el conjunto en términos de cardinalidad. Esto se escribe:
Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A| \le_{\#} |B| y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |B| \le_{\#} |A| , entonces significa que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A| = |B| . Es decir, si el conjunto A es "más pequeño o igual" que B, y B es "más pequeño o igual" que A, entonces deben tener el mismo tamaño.
El cardinal del conjunto vacío (un conjunto que no tiene ningún elemento) se representa como 0:
El primer cardinal infinito es el de los números naturales, y se denota como .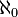
Cardinal del conjunto de partes
Existe una relación interesante entre el cardinal de un conjunto y el conjunto de todos sus posibles subconjuntos (llamado "conjunto de partes"). Si un conjunto tiene 
elementos, entonces su conjunto de partes tendrá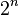 
elementos.
Donde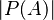 
es el cardinal del conjunto de partes de .
Cardinales infinitos especiales
Algunos conjuntos infinitos tienen cardinales con símbolos especiales:
- El cardinal de los números reales se denota como
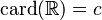. - El cardinal de los números naturales es
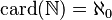(Alef-0). - Existe un cardinal inmediatamente superior a 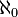, llamado
.
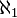Se ha demostrado que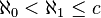 
. Esto significa que el infinito de los números reales es igual o más grande que el siguiente infinito después de los naturales.
Ejemplos de cálculo de cardinales
Conjuntos finitos
Si tenemos el conjunto = {2, 4, 5}, su cardinal es 3. Esto es fácil de ver porque podemos emparejar sus elementos con los números {1, 2, 3}.
Conjuntos infinitos
Números pares
El conjunto de los números pares 
= {
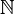∈ | es par } (es decir, {2, 4, 6, ...}) tiene un cardinal de 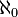. Aunque parezca que hay menos números pares que números naturales (porque los números impares no están en el conjunto de pares), ¡ambos conjuntos tienen el mismo tamaño infinito!
Podemos demostrarlo emparejando cada número natural con un número par:
- 1 se empareja con 2
- 2 se empareja con 4
- 3 se empareja con 6
- ...y así sucesivamente.
Esto muestra que hay una correspondencia uno a uno, por lo tanto, tienen la misma cardinalidad.
Pares ordenados de números naturales
El conjunto de todos los pares ordenados de números naturales (como (1,1), (1,2), (2,1), etc.) también tiene un cardinal de 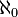. Esto significa que, aunque parezca que hay muchísimos más pares que números naturales, ¡también tienen el mismo tamaño infinito!
Podemos demostrarlo asignando un número natural único a cada par. Por ejemplo, podemos usar la fórmula Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): z = 3^x \cdot 2^y . Como 2 y 3 son números primos, cada par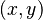 
nos dará un número 
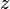diferente. Esto nos permite emparejar cada par con un número natural.
Números racionales
El conjunto de los números racionales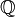 
(fracciones como 1/2, 3/4, -5/7) también tiene un cardinal igual a 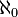. Esto es sorprendente porque los números racionales están "muy juntos" en la recta numérica. Entre dos números reales cualquiera, siempre hay un número racional.
Sin embargo, a pesar de lo "densos" que son, el conjunto de los números racionales tiene el mismo tamaño infinito que el conjunto de los números naturales. Esto se demuestra de manera similar, encontrando una forma de emparejar cada número racional con un número natural.
Aritmética de cardinales
Podemos "sumar" y "multiplicar" cardinales.
- Para la suma, si tienes dos conjuntos que no comparten elementos, el cardinal de su unión (todos los elementos juntos) es la suma de sus cardinales.
- Para la multiplicación, el cardinal del producto cartesiano (todas las combinaciones posibles de elementos de ambos conjuntos) es la multiplicación de sus cardinales.
Cuando trabajamos con conjuntos finitos, estas operaciones son como la suma y multiplicación normales que ya conoces. Pero con los cardinales infinitos, las cosas cambian:
- Si sumas dos cardinales infinitos, el resultado es el cardinal más grande de los dos. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \aleph_0 + \aleph_0 = \aleph_0 .
- Si multiplicas dos cardinales infinitos, el resultado también es el cardinal más grande de los dos. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \aleph_0 \cdot \aleph_0 = \aleph_0 .
También existe la exponenciación de cardinales, que se relaciona con el número de funciones posibles entre dos conjuntos.
|
Véase también
En inglés: Cardinal number Facts for Kids
- Contar
- Álef
- Número ordinal (teoría de conjuntos)
- Número cardinal
