Argumento de la diagonal de Cantor para niños

El argumento de la diagonal de Cantor, también conocido como método de la diagonal, es una idea matemática muy inteligente que el matemático Georg Cantor presentó alrededor de 1891. La usó para demostrar que el conjunto de los números reales no es "numerable".

¿Qué significa que un conjunto no sea numerable? Imagina que quieres hacer una lista de todos los números. Si puedes ponerlos en una lista, uno tras otro, y sabes que tarde o temprano todos aparecerán en esa lista, entonces el conjunto es numerable. Por ejemplo, los números enteros (1, 2, 3,...) son numerables, ¡aunque sean infinitos! Pero Cantor demostró que los números reales no se pueden poner en una lista así. Siempre habrá un número real que se quede fuera de cualquier lista que intentes hacer.

Esta demostración de Cantor no fue la primera en mostrar esto, pero sí fue la más sencilla y elegante. Además, inspiró otras demostraciones matemáticas que también usan una idea similar, por eso se les llama "argumento diagonal".

Los números reales y el argumento de Cantor

La prueba original de Cantor se enfoca en un pequeño pedazo de los números reales: los números que están entre 0 y 1 (como 0.5, 0.12345, 0.999...). Demuestra que este intervalo no es numerable. Esto significa que no podemos hacer una lista completa de todos los números reales que hay entre 0 y 1. Siempre habrá más. Si esto es cierto para un pedacito, ¡imagina para todos los números reales!

La demostración de Cantor usa un método llamado "reducción al absurdo". Esto significa que se parte de una suposición y se demuestra que esa suposición lleva a una contradicción. Si hay una contradicción, la suposición inicial debe ser falsa.

Aquí te explicamos los pasos:

• Paso 1: La suposición. Imaginemos que sí es posible hacer una lista de todos los números reales entre 0 y 1. Si fuera posible, podríamos numerarlos: el primer número, el segundo, el tercero, y así sucesivamente.
• Paso 2: La lista imaginaria. Si nuestra suposición fuera cierta, podríamos escribir una lista infinita de todos esos números. Cada número real entre 0 y 1 se puede escribir como 0. seguido de muchos decimales.

Una lista así podría verse de esta manera:

r₁ = 0. 5 1 0 5 1 1 0...

r₂ = 0. 4 1 3 2 0 4 3...

r₃ = 0. 8 2 4 5 0 2 6...

r₄ = 0. 2 3 3 0 1 2 6...

r₅ = 0. 4 1 0 7 2 4 6...

r₆ = 0. 9 9 3 7 8 3 8...

r₇ = 0. 0 1 0 5 1 3 5...

...

• Paso 3: Construyendo un nuevo número. Ahora viene la parte ingeniosa. Vamos a construir un número real nuevo, al que llamaremos x, que no puede estar en nuestra lista. Para hacerlo, miramos los dígitos en la "diagonal" de nuestra lista:

r₁ = 0. 5 1 0 5 1 1 0... (Tomamos el primer dígito del primer número)

r₂ = 0. 4 1 3 2 0 4 3... (Tomamos el segundo dígito del segundo número)

r₃ = 0. 8 2 4 5 0 2 6... (Tomamos el tercer dígito del tercer número)

r₄ = 0. 2 3 3 0 1 2 6... (Tomamos el cuarto dígito del cuarto número)

r₅ = 0. 4 1 0 7 2 4 6... (Tomamos el quinto dígito del quinto número)

r₆ = 0. 9 9 3 7 8 3 8... (Tomamos el sexto dígito del sexto número)

r₇ = 0. 0 1 0 5 1 3 5... (Tomamos el séptimo dígito del séptimo número)

...

Ahora, para construir nuestro número x, tomamos cada uno de esos dígitos de la diagonal y le cambiamos el valor. Por ejemplo, si el dígito es un 5, lo cambiamos por un 6. Si es un 1, lo cambiamos por un 2. Si es un 9, lo cambiamos por un 0 (o cualquier otro dígito que no sea 9).

Así, si los dígitos de la diagonal son 5, 1, 4, 0, 2, 3, 5..., nuestro nuevo número x sería: x = 0. 6 2 5 1 3 4 6... (cambiando cada dígito por el siguiente, o 9 por 0)

• Paso 4: La contradicción. El número x que acabamos de construir es claramente un número real entre 0 y 1. Pero, ¿dónde está x en nuestra lista?

* No puede ser r₁, porque su primer dígito es diferente (6 en lugar de 5). * No puede ser r₂, porque su segundo dígito es diferente (2 en lugar de 1). * No puede ser r₃, porque su tercer dígito es diferente (5 en lugar de 4). * Y así sucesivamente. Para cualquier número r_n en la lista, el enésimo dígito de x es diferente del enésimo dígito de r_n.

Esto significa que el número x que construimos no está en nuestra lista. ¡Pero habíamos supuesto que la lista contenía a todos los números reales entre 0 y 1! Esto es una contradicción.

• Conclusión: Como nuestra suposición inicial (que se podía hacer una lista de todos los números reales) nos llevó a una contradicción, esa suposición debe ser falsa. Por lo tanto, el conjunto de los números reales no es numerable. Hay "más" números reales de los que podemos contar, incluso si intentamos hacer una lista infinita.

Un ejemplo de cómo funciona el argumento diagonal de Cantor. Dada una lista de números, se puede crear un nuevo número que no está en la lista, al cambiar los dígitos de la diagonal.

Números enteros positivos y el Teorema de Cantor

El argumento de la diagonal de Cantor también está relacionado con el Teorema de Cantor. Este teorema dice que para cualquier conjunto, el conjunto de todos sus posibles subconjuntos (llamado conjunto potencia) es siempre "más grande" que el conjunto original.

Por ejemplo, el argumento de la diagonal de Cantor se puede usar para demostrar que:

Demostración simplificada

Imagina que intentamos hacer una lista de todos los posibles conjuntos que se pueden formar con números enteros positivos (como {1, 2}, {5, 10, 15}, {todos los números pares}, etc.). Si pudiéramos hacer una lista de todos esos conjuntos, se vería así: 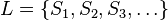Donde 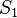es el primer conjunto, 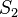el segundo, y así.

Ahora, vamos a construir un nuevo conjunto, al que llamaremos 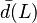, que no puede estar en esa lista. Este nuevo conjunto se forma así: 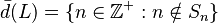Esto significa que 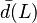contiene todos los números enteros positivos n que no están en el conjunto 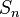de nuestra lista.

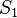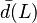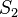Por ejemplo, si es el conjunto {2, 3, 4...} (no contiene el 1), entonces el 1 iría en . Si es el conjunto {1, 2, 3...} (contiene el 2), entonces el 2 no iría en .

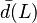Si nuestra lista L fuera realmente completa y contuviera todos los conjuntos de números enteros positivos, entonces 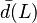debería estar en algún lugar de esa lista. Digamos que 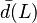es el conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_m en nuestra lista. Entonces, tendríamos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_m = \bar{d}(L) .

Pero esto nos lleva a una contradicción:

• Si el número m está en 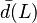, entonces, por la definición de 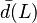, m no debería estar en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_m .
• Pero si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_m = \bar{d}(L) , y m está en 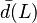, entonces m sí debería estar en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_m .

¡Esto es imposible! m no puede estar y no estar en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): S_m al mismo tiempo. Esta contradicción demuestra que nuestra suposición inicial (que podíamos hacer una lista de todos los conjuntos de números enteros positivos) es falsa. Por lo tanto, el conjunto de todos los conjuntos de números enteros positivos no es numerable.

Véase también

En inglés: Cantor's diagonal argument Facts for Kids