Modelo científico para niños
Un modelo científico es como una versión simplificada o una representación especial de algo que los científicos quieren entender. Puede ser un dibujo, un esquema, un objeto físico o incluso una fórmula matemática. Su objetivo principal es ayudar a los científicos a analizar, describir, explicar y predecir cómo funcionan ciertos fenómenos, sistemas o procesos en el mundo.
Imagina que quieres entender cómo se mueve un planeta alrededor del Sol. Sería muy difícil estudiar el planeta real directamente. En cambio, puedes crear un modelo, como un dibujo o un programa de computadora, que represente el planeta y el Sol, y cómo interactúan. Este modelo te permite hacer pruebas y ver qué pasaría en diferentes situaciones.
Crear modelos es una parte muy importante del trabajo científico. Permite a los investigadores explorar ideas y probar sus hipótesis de una manera controlada.
Contenido
¿Qué diferencia hay entre un modelo y una teoría?
Es importante saber que un modelo científico no es lo mismo que una teoría, aunque están muy relacionados. Una teoría es una explicación más amplia y profunda de cómo funciona algo, basada en muchas observaciones y pruebas. Un modelo es una forma de interpretar o mostrar esa teoría.
Piensa en una teoría como un libro de reglas muy completo sobre cómo funciona el universo. Un modelo sería como un diagrama o un ejemplo específico que te ayuda a entender una parte de esas reglas. Una misma teoría puede tener varios modelos diferentes para explicar sus ideas.
¿Cómo se construye un modelo científico?
Para construir un modelo, los científicos primero hacen algunas suposiciones o hipótesis sobre lo que quieren estudiar. Intentan que el modelo capture las partes más importantes de la realidad, pero también buscan que sea lo suficientemente sencillo como para poder trabajar con él y entenderlo.
El proceso de crear un modelo implica simplificar la realidad. Se dejan de lado algunos detalles menos importantes y se resaltan otros que son clave para entender el fenómeno. Esto es posible porque los modelos se basan en la idea de la analogía, es decir, encontrar similitudes entre lo que se estudia y algo que ya se conoce.
Un modelo se vuelve realmente útil en la ciencia cuando se puede comprobar con observaciones o experimentos precisos.
Tipos de modelos científicos
Los modelos científicos se pueden clasificar según cómo están construidos y cómo funcionan. Aquí te presentamos algunos de los tipos más comunes:
Modelos físicos
Los modelos físicos son representaciones a escala de objetos o sistemas reales. Por ejemplo, una maqueta de un edificio o un prototipo de un coche son modelos físicos. Permiten estudiar cómo se comportaría el objeto real en diferentes situaciones. A veces, la escala no es la misma en todas las direcciones, como en los modelos de terrenos donde la altura se exagera para ver mejor los detalles.
Modelos matemáticos
Estos modelos usan fórmulas y ecuaciones matemáticas para describir fenómenos o las relaciones entre ellos. Son muy comunes en muchas ciencias.
Modelos deterministas
En estos modelos, si conoces los datos de entrada, el resultado siempre será el mismo. Son muy precisos y se usan cuando se cree que se entiende completamente el fenómeno. Un ejemplo es la ley de gravitación universal de Isaac Newton, que permite calcular con exactitud cómo se atraen los objetos.
Modelos estocásticos o probabilísticos
A diferencia de los deterministas, en estos modelos el resultado no es exacto, sino una probabilidad. Se usan cuando hay incertidumbre o cuando el fenómeno tiene un componente aleatorio.
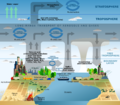
Modelos numéricos
Estos modelos representan la realidad y las condiciones iniciales con números. Luego, usan computadoras para calcular otros números que muestran cómo evolucionaría el fenómeno. Permiten hacer "experimentos" virtuales a través de simulaciones. Un ejemplo es la Simulación numérica del clima.
Modelos gráficos
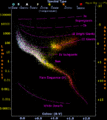
Los modelos gráficos usan dibujos, líneas, vectores o símbolos para mostrar datos, generalmente números. Ayudan a visualizar las relaciones entre diferentes elementos o factores de forma clara. Un ejemplo es un Diagrama de Hertzsprung-Russell, que muestra la relación entre el brillo y el color de las estrellas.
Modelos análogos
Se basan en la idea de que dos sistemas físicos diferentes pueden comportarse de manera similar y ser descritos por las mismas ecuaciones matemáticas. Por ejemplo, antes se usaban redes eléctricas para modelar el flujo de agua subterránea, porque las ecuaciones que describen ambos fenómenos son parecidas.
Modelos conceptuales
Estos modelos son como mapas de ideas y sus relaciones. Se enfocan en los aspectos más importantes de un fenómeno para entenderlo. Implican un alto nivel de abstracción. Ejemplos incluyen el modelo atómico de Bohr, que describe cómo se organizan los electrones alrededor del núcleo de un átomo, o el modelo cíclico de la evolución del Universo.
Partes de un modelo científico
En general, un modelo tiene dos partes principales:
- Reglas para la entrada y salida de datos: Estas reglas definen cómo se toman los datos de la realidad (el "input") y cómo el modelo los procesa para dar un resultado (el "output"). El resultado es una interpretación de cómo las condiciones iniciales afectan la realidad.
- Estructura interna: Es la lógica o el funcionamiento del modelo que conecta el "input" con el "output". Si el mismo "input" siempre produce el mismo "output", el modelo es determinista. Si el mismo "input" puede dar diferentes "outputs", es no determinista.
Estas partes solo tienen sentido dentro de un área específica de la ciencia. Fuera de ese ámbito, el modelo podría no funcionar o sus resultados no tendrían significado.
La caja negra
A veces, en ciencia, se habla de una "caja negra" para referirse a un sistema o proceso cuyo funcionamiento interno no se conoce completamente, pero sí se sabe qué entra (input) y qué sale (output). Es como una caja misteriosa: no ves lo que hay dentro, pero sí lo que le metes y lo que te devuelve.
Las teorías científicas no son "cajas negras" puras, porque siempre intentan explicar el "porqué" de las cosas, no solo el "qué" ocurre. Sin embargo, el concepto de "caja negra" es útil porque permite a los científicos avanzar en su conocimiento sin tener que entender cada pequeño detalle de un sistema complejo de inmediato. Se enfocan en las relaciones de causa y efecto entre lo que entra y lo que sale.
Ejemplos de modelos científicos
Modelo IS-LM
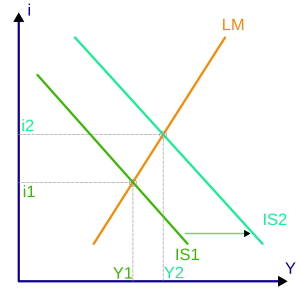
El modelo muestra la interacción entre los mercados reales (curva IS) y los monetarios (curva LM). Ambos mercados interactúan y se influyen mutuamente ya que el nivel de renta determinará la demanda de dinero (y por tanto el precio del dinero o tipo de interés) y el tipo de interés influirá en la demanda de inversión (y por tanto en la renta y la producción real). Por tanto en este modelo se niega la neutralidad del dinero y se requiere que el equilibrio se produzca simultáneamente en ambos mercados.
El modelo IS-LM, está inspirado en las ideas de John Maynard Keynes pero además sintetiza sus ideas con las de los modelos neoclásicos en la tradición de Alfred Marshall. Fue elaborado inicialmente por John Hicks en 1937 y desarrollado y popularizado posteriormente por Alvin Hansen. Las curvas IS-LM permanecen como el ejemplo supremo de la pedagogía de la teoría económica de los tiempos de dominio del pensamiento keynesiano.
El modelo IS-LM es una herramienta usada en macroeconomía (el estudio de la economía a gran escala) para entender cómo se relacionan la producción de un país y las tasas de interés. Ayuda a explicar cómo las decisiones del gobierno sobre impuestos y gasto (política fiscal) o sobre el dinero en circulación (política monetaria) pueden afectar la economía. Se representa con dos líneas que se cruzan, llamadas IS y LM, que muestran el equilibrio entre los mercados de bienes y servicios y los mercados de dinero.
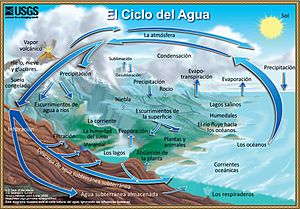
Modelo de escorrentía
Un modelo de escorrentía es una representación que forma parte del ciclo hidrológico en cuanto al fenómeno de la escorrentía superficial de una cuenca hidrográfica. El modelo se usa mayormente para entender el proceso de escurrimiento y para pronosticarlo con el propósito de regularizar el uso del agua o diseñar obras hidráulicas para el control de inundaciónes.
Aunque se podrían hacer modelos a escala, la gran mayoría de los modelos de la escorrentía son modelos matemáticos.
Un modelo de escorrentía ayuda a entender cómo el agua de la lluvia se mueve sobre la superficie de una cuenca hidrográfica (un área de tierra donde toda el agua fluye hacia un mismo río o lago). Estos modelos son muy útiles para predecir inundaciónes o para planificar cómo usar el agua de manera eficiente. La mayoría de los modelos de escorrentía son modelos matemáticos que usan ecuaciones para simular el movimiento del agua.
Galería de imágenes
-
Ejemplo de un modelo científico. Un esquema de los procesos químicos y de transporte relacionados con la composición atmosféricas.
-
Modelado de plegamientos geológicos en Instituto Geofísico AS CR, República Checa.
-
Diagrama de Hertzsprung-Russell: Representación conceptual de luminosidad/magnitud absoluta en relación con el color de las estrellas.
-
Animación mostrando la agitación térmica de un gas. Cinco partículas han sido coloreadas de rojo para facilitar el seguimiento de sus movimientos.
-
Modelo de una colisión de partículas
-
Esquema de caja negra.
-
Esquematización del ciclo hidrológico
Véase también
En inglés: Scientific model Facts for Kids
- Mapa conceptual
- Modelo matemático
- Simulación
- VUE
- Visualización científica
- Modelo análogo
Referencias
