Lógica modal para niños
Una lógica modal es un sistema especial de lógica que nos ayuda a entender y trabajar con ideas como "es necesario que" o "es posible que". Imagina que quieres decir que "es necesario que 2 + 2 = 4". La frase "es necesario que" es un operador modal. Nos dice algo sobre la verdad de la afirmación.
No es lo mismo decir "está lloviendo" que decir "siempre está lloviendo". La palabra "siempre" también es un tipo de operador modal que indica que algo es verdad en todo momento.
En este artículo, nos centraremos en las lógicas modales que usan las ideas de "necesidad" y "posibilidad". Estas lógicas son como extensiones de la lógica clásica, que es la lógica que usamos normalmente. Otras lógicas extendidas incluyen la lógica deóntica (sobre lo que debe o no debe ser), la lógica temporal (sobre el tiempo) y la lógica epistémica (sobre el conocimiento).
Contenido
¿Cómo funciona una lógica modal?
Para entender la lógica modal, podemos verla como un lenguaje con sus propias reglas y símbolos.
Símbolos especiales
La lógica modal añade dos símbolos nuevos a la lógica proposicional (que trata con afirmaciones simples):
- El símbolo
 (un cuadrado) significa "es necesario que".
(un cuadrado) significa "es necesario que". - El símbolo
 (un diamante) significa "es posible que".
(un diamante) significa "es posible que".
Estos símbolos se colocan antes de una afirmación. Por ejemplo, si 'p' significa "está lloviendo":
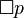 se lee "es necesario que esté lloviendo".
se lee "es necesario que esté lloviendo".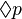 se lee "es posible que esté lloviendo".
se lee "es posible que esté lloviendo".
Estos dos símbolos están relacionados. Si algo no es posible que no ocurra, entonces es necesario que ocurra. Y si algo no es necesario que ocurra, entonces es posible que no ocurra.
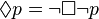 (Es posible que 'p' es lo mismo que decir que no es necesario que no 'p').
(Es posible que 'p' es lo mismo que decir que no es necesario que no 'p').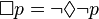 (Es necesario que 'p' es lo mismo que decir que no es posible que no 'p').
(Es necesario que 'p' es lo mismo que decir que no es posible que no 'p').
Esto significa que, en realidad, solo necesitamos uno de los dos símbolos para definir el otro.
Reglas para construir frases
La lógica modal tiene reglas para formar "fórmulas bien formadas", que son como oraciones correctas en su lenguaje. Son las mismas reglas que en la lógica proposicional, pero con una adición importante:
- Si una afirmación (
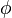 ) está bien construida, entonces ponerle
) está bien construida, entonces ponerle  delante (
delante ( ) también resulta en una afirmación bien construida.
) también resulta en una afirmación bien construida.
Por ejemplo, estas son fórmulas bien formadas:
 (Es posible que si 'p' entonces es necesario que 'q').
(Es posible que si 'p' entonces es necesario que 'q').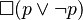 (Es necesario que 'p' o no 'p' sea verdad).
(Es necesario que 'p' o no 'p' sea verdad).
Reglas para sacar conclusiones
Una regla importante en lógica modal es la regla N (o de Necesitación). Dice que si una afirmación es un teorema (algo que se ha demostrado que es siempre verdad), entonces también es un teorema que "es necesario que" esa afirmación sea verdad.
Además, se usa el modus ponens, una regla de la lógica proposicional que dice que si tienes "si A entonces B" y tienes "A", entonces puedes concluir "B".
Axiomas: Las verdades básicas
Los axiomas son como las verdades fundamentales que no necesitan ser demostradas. En lógica modal, hay diferentes conjuntos de axiomas, y cada conjunto crea un sistema de lógica modal distinto. La elección de axiomas depende de lo que se quiera demostrar.
Aquí hay algunos axiomas conocidos:
| Nombre | Axioma | Lectura sencilla |
|---|---|---|
| K | 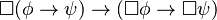 |
Si es necesario que (si 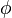 entonces entonces 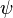 ), entonces si es necesario que ), entonces si es necesario que 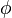 , también es necesario que , también es necesario que 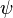 . . |
| T (o M) |  |
Si es necesario que 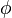 , entonces , entonces 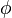 es verdad. es verdad. |
| 4 | 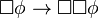 |
Si es necesario que 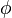 , entonces es necesario que sea necesario que , entonces es necesario que sea necesario que 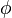 . . |
| 5 | 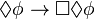 |
Si es posible que 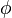 , entonces es necesario que sea posible que , entonces es necesario que sea posible que 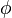 . . |
| B | 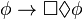 |
Si 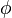 es verdad, entonces es necesario que sea posible que es verdad, entonces es necesario que sea posible que 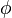 . . |
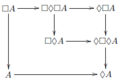
Diferentes combinaciones de estos axiomas forman distintos sistemas de lógica modal. El sistema más básico se llama K (por Saul Kripke) y solo usa el axioma K. Otros sistemas más "fuertes" se construyen añadiendo más axiomas a K.
| Sistema | Axiomas |
|---|---|
| K | K |
| T | K, T |
| S4 | K, T, 4 |
| S5 | K, T, 5 |
| B | K, T, B |
Semántica: El significado de los mundos posibles
Para entender cómo funcionan estas lógicas, usamos la idea de "mundos posibles". Imagina que hay muchas realidades o situaciones diferentes. A esto lo llamamos mundos posibles.
Una interpretación de la lógica modal incluye:
- W: Un conjunto de mundos posibles. Piensa en ellos como diferentes escenarios o situaciones.
- R: Una relación de accesibilidad entre los mundos. Esto significa que desde un mundo, puedes "acceder" o "llegar" a otros mundos. Por ejemplo, si estás en un mundo donde decides qué comer, puedes acceder a un mundo donde comes pizza o a otro donde comes pasta. Pero si ya estás en un mundo donde estás comiendo pizza, quizás no puedas acceder a un mundo donde estás comiendo pasta al mismo tiempo.
- V: Una función que dice si una afirmación es verdadera o falsa en cada mundo posible. Una afirmación puede ser verdadera en un mundo y falsa en otro.
Los mundos posibles son clave para entender los operadores modales:
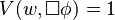 (Es necesario que
(Es necesario que 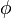 es verdad en el mundo 'w') si y solo si
es verdad en el mundo 'w') si y solo si 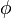 es verdad en todos los mundos posibles a los que se puede acceder desde 'w'.
es verdad en todos los mundos posibles a los que se puede acceder desde 'w'.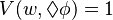 (Es posible que
(Es posible que 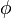 es verdad en el mundo 'w') si y solo si
es verdad en el mundo 'w') si y solo si 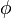 es verdad en al menos un mundo posible al que se puede acceder desde 'w'.
es verdad en al menos un mundo posible al que se puede acceder desde 'w'.
Consecuencia lógica y deducción
En lógica, queremos saber cuándo una conclusión se sigue de unas premisas. Esto se llama consecuencia lógica. En la lógica modal, como la verdad depende de los mundos posibles, la consecuencia lógica también lo hace. Un argumento es válido si, en cualquier mundo posible y en cualquier interpretación, si las premisas son verdaderas, la conclusión también lo es.
Un sistema deductivo es un conjunto de reglas que nos permiten llegar a conclusiones basándonos solo en la forma de las afirmaciones. El sistema deductivo básico para la lógica modal es el sistema K.
Restricciones en la relación de accesibilidad
Los diferentes sistemas de lógica modal (como T, S4, S5) se obtienen añadiendo axiomas al sistema K. Cada uno de estos axiomas impone una condición especial a la relación de accesibilidad (R) entre los mundos posibles.
Por ejemplo:
| Axioma | R es... | Significado |
|---|---|---|
| T | Reflexiva | Cada mundo puede acceder a sí mismo. |
| 4 | Transitiva | Si puedes ir de A a B, y de B a C, entonces puedes ir de A a C. |
| 5 | Euclidiana | Si puedes ir de A a B, y de A a C, entonces puedes ir de B a C. |
| B | Simétrica | Si puedes ir de A a B, también puedes ir de B a A. |
Así, el sistema S4, que incluye los axiomas T y 4, es para interpretaciones donde la relación de accesibilidad es reflexiva y transitiva.
Historia de la lógica modal
La idea de la lógica modal es muy antigua, se remonta a Aristóteles en la antigua Grecia. Él ya hablaba de la necesidad y la posibilidad en sus escritos. Más tarde, Avicena desarrolló un sistema de lógica que incluía el tiempo.
La lógica modal moderna comenzó a principios del siglo XX, cuando lógicos como Clarence Irving Lewis buscaron formas de entender mejor las frases como "si... entonces" en el lenguaje natural. Lewis propuso la "implicación estricta", que es una conexión más fuerte entre dos ideas que la que se usa en la lógica clásica.
Durante un tiempo, la lógica modal no fue muy popular. Pero en los años sesenta, el trabajo de Saul Kripke fue muy importante. Kripke introdujo la idea de la semántica de mundos posibles, que es la forma en que entendemos y analizamos la lógica modal hoy en día. Esta herramienta ha sido muy útil para estudiar no solo la necesidad y la posibilidad, sino también el tiempo, el conocimiento y lo que se debe hacer.
Véase también
 En inglés: Modal logic Facts for Kids
En inglés: Modal logic Facts for Kids
- Lógica proposicional
- Lógica de primer orden
- Lógica deóntica
- Lógica temporal
- Lógica epistémica
- Lógica doxástica
- Implicación
- Gottfried Leibniz
Galería de imágenes