Relación reflexiva para niños

En matemáticas, una relación reflexiva es un tipo especial de conexión o vínculo entre los elementos de un conjunto. Imagina que tienes un grupo de cosas, como números o personas. Una relación reflexiva significa que cada elemento de ese grupo está relacionado consigo mismo. Por ejemplo, si la relación es "es igual a", entonces cada número es igual a sí mismo (5 es igual a 5).

Cuando una relación es lo opuesto a una reflexiva, es decir, cuando ningún elemento de un conjunto está relacionado consigo mismo, se le llama relación irreflexiva o antirreflexiva. Por ejemplo, la relación "ser padre de" es antirreflexiva, porque nadie puede ser su propio padre.

Plantilla:Ficha de concepto matemático

¿Cómo se representa una relación reflexiva?

Una relación reflexiva o irreflexiva se puede mostrar de diferentes maneras, y cada una tiene una característica especial que nos dice si es reflexiva o no.

Pares ordenados

Cuando representamos una relación como una lista de pares ordenados (como (1,1), (2,3)), una relación reflexiva siempre incluirá pares donde el primer y el segundo elemento son iguales para cada elemento del conjunto. Por ejemplo, si el conjunto es {1, 2, 3}, una relación reflexiva tendría (1,1), (2,2) y (3,3). Una relación irreflexiva, en cambio, nunca tendrá estos pares.

Matrices de adyacencia

Si usamos una matriz de adyacencia para representar la relación (una tabla de números donde 1 significa que hay una conexión y 0 que no), en una relación reflexiva, todos los números en la línea diagonal principal (de arriba a la izquierda a abajo a la derecha) serán 1. Esto significa que cada elemento está conectado consigo mismo. En una relación irreflexiva, todos los números en esa diagonal serán 0.

Grafos

En un grafo (un dibujo con puntos y líneas que muestran las conexiones), una relación reflexiva tendrá un "bucle" (una línea que va y vuelve al mismo punto) en cada uno de sus nodos (los puntos). Esto indica que cada elemento se relaciona consigo mismo. Una relación irreflexiva no tendrá ningún bucle en sus nodos.

Ejemplos de relaciones reflexivas e irreflexivas

Veamos algunos ejemplos para entenderlo mejor:

• "Mayor o igual que" (≥) y "Menor o igual que" (≤): Estas relaciones son reflexivas. Por ejemplo, 5 es mayor o igual que 5, y 3 es menor o igual que 3.
• "Mayor estricto que" (>) y "Menor estricto que" (<): Estas relaciones son irreflexivas. Por ejemplo, 5 no es mayor que 5, y 3 no es menor que 3.
• "Igualdad" (=): Esta es una relación reflexiva. Cualquier cosa es igual a sí misma.
• "Inclusión de conjuntos" (⊆): Si tienes conjuntos, un conjunto siempre está incluido en sí mismo. Por lo tanto, es reflexiva.
• "Divisibilidad" (/): En los números naturales (sin incluir el cero), un número siempre es divisible por sí mismo. Por ejemplo, 7 es divisible por 7. Así que es reflexiva.
• "Paralelismo" (||) entre rectas: Si tienes líneas en un plano, una línea siempre es paralela a sí misma. Es una relación reflexiva.
• "Perpendicularidad" (⊥) entre rectas: Una línea no puede ser perpendicular a sí misma. Por lo tanto, esta relación es irreflexiva.
• "Ser padre de" o "Ser madre de": Nadie puede ser su propio padre o madre. Estas relaciones son irreflexivas.

Véase también

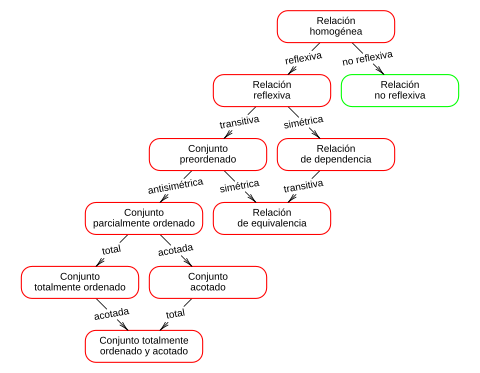
En inglés: Reflexive relation Facts for Kids Propiedades de una relación binaria homogénea:

• Relación irreflexiva
• Relación simétrica
• Relación antisimétrica
• Relación transitiva
• Relación total
• Relación bien fundada