Teoría de la computación para niños
La teoría de la computación es una parte de la informática y las matemáticas que estudia qué problemas se pueden resolver con computadoras y qué tan rápido o con cuánta memoria se pueden resolver. Imagina que es como el estudio de las reglas y límites de lo que una computadora puede hacer.
Para entender esto, los expertos usan modelos matemáticos de las computadoras, como la máquina de Turing. Este modelo es muy importante porque, aunque es sencillo, puede representar lo que cualquier computadora "razonable" puede hacer. Aunque una máquina de Turing parece tener memoria infinita, para resolver cualquier problema real solo necesita una cantidad finita de memoria. Esto significa que si un problema puede ser resuelto por una máquina de Turing, también puede ser resuelto por una computadora real con suficiente memoria.
Contenido
Teoría de la Computación
La teoría de la computación nos ayuda a entender cómo funcionan los procesos que una computadora realiza. Piensa en ello como un conjunto de ideas y reglas que nos permiten simular y organizar cómo las computadoras resuelven problemas.
¿Qué es un Modelo de Computación?
Para estudiar la computación de forma precisa, los científicos usan una versión simplificada y matemática de las computadoras, llamada modelo de computación. Hay varios modelos, pero el más conocido es la máquina de Turing. Este modelo es fácil de entender y sirve para demostrar qué se puede calcular y qué no.
Ramas Principales de la Teoría de la Computación
La teoría de la computación se divide en varias áreas importantes que nos ayudan a entender mejor las computadoras y sus capacidades.
Teoría de Autómatas: ¿Cómo funcionan las máquinas?
Esta rama nos da modelos matemáticos para entender qué es una "computadora" o un "algoritmo" de forma simple. Así podemos analizar qué pueden hacer y cuáles son sus límites. Estos modelos son clave en muchas aplicaciones de la informática, como el procesamiento de texto, los programas que traducen código (compiladores), el diseño de hardware y la inteligencia artificial.
Existen otros tipos de autómatas, pero se ha demostrado que la máquina de Turing puede simular a todos ellos. Por eso, la máquina de Turing se considera el modelo universal de una computadora.
Teoría de la Computabilidad: ¿Qué problemas se pueden resolver?
Esta parte de la teoría explora hasta dónde podemos llegar al resolver problemas con algoritmos. Un algoritmo es como una receta con pasos claros para resolver algo. Es sorprendente descubrir que hay problemas que, por más que lo intentemos, ninguna computadora podrá resolver con un algoritmo.
La teoría de la computabilidad nos ayuda a no perder tiempo intentando resolver problemas que son "imposibles" para las computadoras. Los problemas se clasifican según su dificultad:
Tipos de Problemas Computacionales
- Los computables (o decidibles) son aquellos para los que siempre existe un algoritmo que los resuelve. Si hay una solución, el algoritmo la encuentra; si no, el algoritmo lo sabe.
- Los semicomputables (o enumerables recursivamente) son aquellos para los que un algoritmo puede encontrar una solución si existe. Pero si no hay solución, el algoritmo nunca termina de buscar (entra en un bucle infinito). Un ejemplo famoso es el problema de la parada, que pregunta si un programa de computadora terminará o seguirá ejecutándose para siempre.
- Los incomputables son problemas para los que no existe ningún algoritmo que los pueda resolver, sin importar si tienen o no solución.
Para clasificar estos problemas, se usa el concepto de reducibilidad. Esto significa que si puedes resolver el problema B, entonces también puedes resolver el problema A. Es como decir que el problema A "no es más difícil" que el problema B.
Teoría del Lenguaje Formal: ¿Cómo se comunican las computadoras?
Esta rama de las matemáticas describe los lenguajes como un conjunto de operaciones sobre un alfabeto (como las letras y símbolos que usamos). Está muy relacionada con la teoría de autómatas, ya que los autómatas se usan para crear y entender estos lenguajes formales.
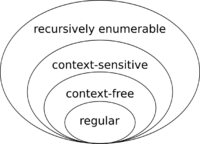
Existen diferentes tipos de lenguajes formales, cada uno más complejo que el anterior. Esto se conoce como la jerarquía de Chomsky. Como los autómatas son modelos de computación, los lenguajes formales son la forma preferida de describir cualquier problema que deba ser calculado por una computadora.
Teoría de la Complejidad Computacional: ¿Qué tan rápido se resuelven los problemas?
Aunque un problema sea computable, a veces no se puede resolver en la práctica porque necesita demasiada memoria o mucho tiempo. La teoría de la complejidad computacional estudia cuánta memoria, tiempo y otros recursos necesita una computadora para resolver un problema. Esto nos ayuda a entender por qué algunos problemas son más difíciles que otros.
Uno de los grandes logros de esta rama es clasificar los problemas según su dificultad, como si fuera una tabla periódica. Esta clasificación se hace en clases de complejidad.
Esta teoría es útil en casi todas las áreas donde se usan computadoras, porque los investigadores no solo quieren resolver un problema, sino resolverlo de la manera más rápida y eficiente posible. También se usa en criptografía, donde se busca que descifrar un código secreto sea muy difícil, a menos que tengas la contraseña.
Para saber cuánto tiempo y espacio necesita un algoritmo, los informáticos miden el tiempo o el espacio en función del tamaño del problema. Por ejemplo, buscar un número en una lista larga se vuelve más difícil a medida que la lista crece. Si la lista tiene "n" números, podríamos tener que revisar todos los números. Entonces, el tiempo que tarda el ordenador crece de forma lineal con el tamaño del problema.
Para simplificar esto, los informáticos usan la notación Big O. Esta notación permite comparar la eficiencia de los algoritmos sin preocuparse por los detalles de una máquina específica, sino solo por cómo se comportan cuando los problemas son muy grandes. Así, en el ejemplo anterior, diríamos que el problema requiere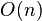 
pasos para resolverse.
Uno de los problemas abiertos más importantes en la informática es si una clase de problemas llamada NP puede resolverse de forma eficiente. Esto se discute en el problema P vs. NP, que es uno de los siete Problemas del milenio propuestos por el Clay Mathematics Institute en el año 2000.
Otras Áreas de Estudio
- Modelos de cómputo: Estudia diferentes formas de entender cómo se realiza un cálculo. Incluye modelos como las funciones recursivas y los cálculo lambda, además de los lenguajes de programación.
- Teoría algorítmica de la información: Se enfoca en la dificultad de describir una secuencia de datos (como un texto) usando un algoritmo. La dificultad se mide por la longitud de la descripción más corta.
- Especificación y verificación formal: Busca métodos para asegurar que un problema esté bien definido y que la solución algorítmica sea correcta.
- Teoría del aprendizaje computacional: Busca algoritmos que permitan a las computadoras aprender y cambiar su comportamiento por sí mismas, basándose en ejemplos. Esto se llama aprendizaje supervisado.
- Teoría de tipos: Clasifica las expresiones y valores en los lenguajes de programación usando herramientas de la teoría de lenguajes formales.
Historia de la Teoría de la Computación
La teoría de la computación comenzó a principios del siglo XX, antes de que se inventaran las computadoras electrónicas. En esa época, varios matemáticos se preguntaban si existía un método universal para resolver todos los problemas matemáticos. Para responder a esto, necesitaban definir qué era exactamente un "método para resolver problemas", es decir, una definición formal de "algoritmo".
Algunos modelos formales fueron propuestos por pioneros como Alonzo Church, Kurt Gödel y Alan Turing. Se ha demostrado que estos modelos son equivalentes, lo que significa que pueden simular los mismos algoritmos, aunque de diferentes maneras. Los lenguajes de programación modernos también han demostrado ser equivalentes a estos modelos. Esto apoya la Tesis de Church-Turing, que sugiere que cualquier algoritmo que exista puede ser simulado por una máquina de Turing.
Uno de los primeros descubrimientos importantes de esta teoría fue que existen problemas imposibles de resolver con algoritmos, siendo el problema de la parada el más famoso. Para estos problemas, no hay ni habrá un algoritmo que los resuelva, sin importar cuánto tiempo o memoria tenga una computadora. Además, con la llegada de las computadoras modernas, se vio que algunos problemas que eran resolubles en teoría, eran imposibles en la práctica porque sus soluciones requerían cantidades de tiempo o memoria poco realistas.
Galería de imágenes
-
Representación artística de una máquina de Turing. Las máquinas de Turing se utilizan frecuentemente como modelos teóricos de computación
Véase también
En inglés: Theory of computation Facts for Kids
