Cota superior asintótica para niños

Una cota superior asintótica es una herramienta matemática que nos ayuda a entender cómo se comporta una función cuando sus valores se hacen muy, muy grandes. Imagina que tienes una función que describe el tiempo que tarda un programa de computadora en hacer una tarea. La cota superior asintótica nos dice que, a partir de cierto punto, el tiempo que tarda ese programa nunca superará un límite que podemos calcular.

Para hablar de esto, usamos algo llamado la notación O grande (se escribe O(g(x))). Esta notación nos permite decir que una función f(x) (por ejemplo, el tiempo de un programa) no crece más rápido que otra función g(x) (nuestro límite), si ignoramos algunas constantes y nos fijamos solo en lo que pasa cuando los números son muy grandes.

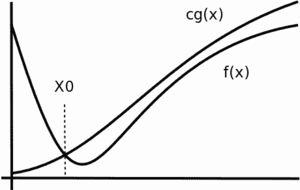
Formalmente, decimos que una función f(x) pertenece a O(g(x)) si existe un número positivo c y un valor x₀ tales que, para todos los valores de x mayores o iguales a x₀, la función f(x) es menor o igual que c veces g(x). Esto significa que f(x) es "más lenta" o "más pequeña" que g(x) a partir de cierto punto, si multiplicamos g(x) por una constante.

Esta idea es muy importante en la Teoría de la complejidad computacional. Nos ayuda a clasificar los algoritmos (las instrucciones que siguen los programas) según lo eficientes que son. Así, podemos saber si un programa será rápido o lento cuando maneje muchos datos.

f(x)=O(g(x)).

Aunque O(g(x)) es un conjunto de funciones, es común escribir f(x)=O(g(x)) en lugar de f(x)∈O(g(x)). Esto es porque la forma en que se comportan las funciones es lo que nos interesa. La imagen de al lado muestra cómo una función f(x) se mantiene por debajo de c veces g(x) cuando x crece.

La cota superior asintótica se relaciona con otras cotas: la Cota inferior asintótica (notación Ω) y la Cota ajustada asintótica (notación Θ). Si una función f(x) es igual a Θ(g(x)), significa que f(x) está acotada tanto por arriba como por abajo por g(x), es decir, f(x)=O(g(x)) y f(x)=Ω(g(x)).

Propiedades de la Notación O Grande

La notación O grande tiene algunas reglas que nos ayudan a trabajar con ella. Aquí te mostramos algunas de las más importantes:

• Si una función f₁ no crece más rápido que g₁, y g₁ no crece más rápido que g₂, entonces f₁ tampoco crece más rápido que g₂.
• Si f₁ no crece más rápido que g₁, y f₂ no crece más rápido que g₂, entonces el producto de f₁ y f₂ no crece más rápido que el producto de g₁ y g₂.
• Si sumamos dos funciones, f₁ y f₂, y cada una tiene su propia cota superior, entonces la suma no crecerá más rápido que la función más grande de las dos cotas.
• Si multiplicamos una función por un número que no sea cero, su cota superior asintótica sigue siendo la misma.

Ejemplos Prácticos

Para entender mejor, veamos algunos ejemplos:

• Imagina la función f(x) = x + 10. Esta función puede ser acotada superiormente por g(x) = x². Esto significa que, a partir de cierto valor de x (aproximadamente 3.7), x + 10 siempre será menor o igual que x². Por lo tanto, decimos que x + 10 = O(x²). Sin embargo, x² no es una cota superior para x + 10, es decir, x² ≠ O(x + 10). Esto nos enseña que la relación de la notación O grande no es simétrica.
• La función 200x está acotada superiormente por x². Esto quiere decir que, cuando x se hace muy grande, el valor de 200x se vuelve insignificante comparado con el de x².

Órdenes Comunes de Crecimiento

En el análisis de algoritmos, usamos diferentes "órdenes" para describir la eficiencia de los programas. Aquí te mostramos algunos de los más comunes, ordenados de los más rápidos a los más lentos (donde n representa el tamaño de la entrada de datos):

Notación	Nombre
O(1)	Orden constante (el tiempo no cambia con el tamaño de la entrada)
O(log log n)	Orden sublogarítmica (muy rápido, crece muy poco)
O(log n)	Orden logarítmica (rápido, por ejemplo, buscar en un diccionario)
O(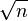)	Orden sublineal (más rápido que lineal, pero más lento que logarítmico)
O(n)	Orden lineal o de primer orden (el tiempo crece directamente con el tamaño de la entrada)
O(n · log n)	Orden lineal logarítmica (un poco más lento que lineal, pero aún eficiente)
O(n2)	Orden cuadrática o de segundo orden (el tiempo crece con el cuadrado del tamaño de la entrada, puede ser lento para entradas grandes)
O(n3), ...	Orden cúbica o de tercer orden, ... (aún más lento)
O(nc)	Orden potencial fija (o polinomial) (el tiempo crece como una potencia de n)
O(cn), n > 1	Orden exponencial (muy lento, el tiempo crece muy rápido con el tamaño de la entrada)
O(n!)	Orden factorial (extremadamente lento, solo para entradas muy pequeñas)
O(nn)	Orden potencial exponencial (aún más lento que factorial)

Véase también

En inglés: Big O notation Facts for Kids

• Cota inferior asintótica
• Cota ajustada asintótica
• Notación de Landau