Problema de la parada para niños

El problema de la parada es una pregunta muy importante en el mundo de la computación. Imagina que tienes un programa de computadora y quieres saber si ese programa terminará de funcionar en algún momento o si seguirá ejecutándose para siempre, sin detenerse. El problema de la parada consiste precisamente en esto: ¿existe un programa especial que pueda decirnos si cualquier otro programa, con una entrada específica, se detendrá o no?

En 1936, un matemático muy famoso llamado Alan Turing demostró que es imposible crear un programa así. Es decir, no hay ninguna computadora ni programa que pueda resolver el problema de la parada para todos los programas posibles. A esto se le llama ser un problema "indecidible" o "no computable".

¿Por qué es importante el problema de la parada?

Cuando usas una computadora, a veces un programa se "congela" o se queda "trabado". Esto ocurre porque el programa ha entrado en un bucle infinito, lo que significa que repite una y otra vez las mismas instrucciones sin llegar a un final. Sería genial tener un programa que pudiera avisarnos de antemano si otro programa se va a quedar atascado, ¿verdad?

La pregunta clave es:

• ¿Existe un programa "P" que, al darle cualquier otro programa "Q" y sus datos de entrada "X", pueda decirnos si "Q" con "X" terminará de funcionar (dando un 1) o si se quedará en un bucle infinito (dando un 0)?

Saber si existe este programa "P" es, en pocas palabras, el problema de la parada.

Es importante entender que esto no significa que nunca podamos saber si un programa específico termina. ¡Claro que sí podemos! Los programadores a menudo demuestran que sus programas funcionan correctamente y terminan. Lo que Alan Turing demostró es que no hay una forma automática y general de saber si *todos* los programas posibles terminarán. No se puede crear un programa que revise cualquier otro programa y siempre dé una respuesta correcta sobre si se detendrá o no.

El estudio de cómo demostrar que los programas terminan se llama Análisis de Terminación. Es un campo muy útil para asegurarse de que los programas funcionen bien.

¿Por qué no se puede resolver el problema de la parada?

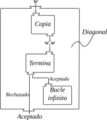
La razón por la que no se puede resolver el problema de la parada es un poco complicada, pero se basa en una idea lógica llamada "argumento diagonal", que es como una paradoja.

Imagina por un momento que sí existe un programa mágico al que llamaremos "DetectorDeParada". Este programa "DetectorDeParada" recibe como entrada el código de cualquier programa (digamos, "P") y los datos que ese programa "P" va a usar (digamos, "X"). Después de un tiempo, "DetectorDeParada" nos diría: "Verdadero" si "P" con "X" termina, o "Falso" si "P" con "X" nunca termina.

Ahora, vamos a crear un nuevo programa, al que llamaremos "Paradoja". Este programa "Paradoja" hará lo siguiente:

• Recibe como entrada el código de un programa (digamos, "W").
• Usa nuestro "DetectorDeParada" para preguntarle: "¿El programa 'W' termina si se le da su propio código 'W' como entrada?".
• Si "DetectorDeParada" dice que "W" sí termina, entonces nuestro programa "Paradoja" entra en un bucle infinito (nunca termina).
• Si "DetectorDeParada" dice que "W" nunca termina, entonces nuestro programa "Paradoja" sí termina.

En resumen, el programa "Paradoja" está diseñado para hacer lo contrario de lo que "DetectorDeParada" le dice sobre el programa "W" cuando "W" se ejecuta con su propio código.

Ahora viene la parte interesante: ¿Qué pasa si le damos al programa "Paradoja" su propio código como entrada?

• Si "Paradoja" termina cuando se ejecuta con su propio código...

* Según su diseño, esto solo ocurre si "DetectorDeParada" dijo que "Paradoja" *no* terminaba con su propio código. * ¡Pero esto es una contradicción! Si termina, no puede ser que no termine.

• Si "Paradoja" no termina (entra en un bucle infinito) cuando se ejecuta con su propio código...

* Según su diseño, esto solo ocurre si "DetectorDeParada" dijo que "Paradoja" *sí* terminaba con su propio código. * ¡Otra contradicción! Si no termina, no puede ser que sí termine.

Como llegamos a una contradicción en ambos casos, la única conclusión posible es que nuestra suposición inicial era incorrecta. Es decir, el programa "DetectorDeParada" no puede existir. Por lo tanto, es imposible crear un programa que resuelva el problema de la parada para todos los programas posibles.

Galería de imágenes

• 

  Una máquina hipotética que podría resolver el problema de la parada.

• 

  La máquina "Diagonal" que usa la máquina "Termina" para crear una paradoja.

Véase también

En inglés: Halting problem Facts for Kids