Divisibilidad para niños
En matemáticas, cuando hablamos de números enteros, decimos que un número b es divisible entre otro número a (que no sea cero) si al dividir b entre a, el resultado es exacto, es decir, el resto es cero.
Esto se puede escribir como 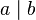 , que significa "a divide a b", o "a es un divisor de b". También podemos decir que "b es un múltiplo de a". Por ejemplo, 6 es divisible entre 3, porque 3 multiplicado por 2 da 6. Pero 6 no es divisible entre 4, porque al dividir 6 entre 4, el resto no es cero.
, que significa "a divide a b", o "a es un divisor de b". También podemos decir que "b es un múltiplo de a". Por ejemplo, 6 es divisible entre 3, porque 3 multiplicado por 2 da 6. Pero 6 no es divisible entre 4, porque al dividir 6 entre 4, el resto no es cero.
Cualquier número natural es divisible entre 1 y entre sí mismo. Los números mayores que 1 que solo tienen estos dos divisores se llaman números primos. Los que tienen más de dos divisores se llaman números compuestos.
| Divisibilidad |
|
Contenido
¿Qué significa que un número sea divisible?
Un número entero a es divisible entre otro número entero b (que no sea cero) si podemos encontrar un número entero q tal que al multiplicar b por q obtenemos a. Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a = b \cdot q .
Cuando esto ocurre, decimos que b divide a a, y lo escribimos como 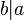 . Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 | 12 es cierto porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 12 = 3 \cdot 4 . Pero
. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 | 12 es cierto porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 12 = 3 \cdot 4 . Pero 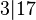 no es cierto, porque no hay un número entero que, multiplicado por 3, dé 17. Si b no es divisor de a, se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b \nmid a . Es importante saber que ningún número puede ser dividido por cero, excepto el propio cero.
no es cierto, porque no hay un número entero que, multiplicado por 3, dé 17. Si b no es divisor de a, se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b \nmid a . Es importante saber que ningún número puede ser dividido por cero, excepto el propio cero.
¿Qué es un divisor propio?
Un divisor propio de un número entero n es cualquier divisor de n que sea diferente de n mismo. El número n se considera un divisor "impropio" de sí mismo.
Por ejemplo, los divisores propios del número 28 son 1, 2, 4, 7 y 14. Si consideramos también los números negativos, los divisores propios serían -14, -7, -4, -2, -1, 1, 2, 4, 7, 14.
Hay algunos casos especiales:
- 1 y -1 son divisores de todos los números enteros.
- Cada número entero es divisor de 0.
- Los números divisibles entre 2 se llaman pares, y los que no lo son se llaman impares.
- Si un divisor d de a solo tiene como divisores a 1 y a sí mismo, entonces d es un divisor primo de a. El 1 es el único número entero que tiene un solo divisor positivo.
Propiedades importantes de la divisibilidad
Las propiedades nos ayudan a entender cómo funciona la divisibilidad entre números enteros. Si tenemos tres números enteros cualesquiera, a, b y c, se cumplen estas reglas:
- Propiedad reflexiva: Si a no es cero, entonces a siempre se divide a sí mismo (
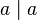 ).
). - Igualdad de valores absolutos: Si a divide a b y b divide a a, entonces el valor absoluto de a es igual al valor absoluto de b (es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |a|= |b| ). Esto significa que son el mismo número o uno es el negativo del otro.
- Propiedad transitiva: Si a divide a b y b divide a c, entonces a también divide a c (
 ).
). - Relación de tamaño: Si a divide a b y b no es cero, entonces el valor absoluto de a es menor o igual que el valor absoluto de b (
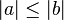 ).
). - Divisibilidad de sumas y restas: Si a divide a b y a divide a c, entonces a también divide a la suma o resta de b y c (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a\mid b \pm c ).
- Divisibilidad por cero y por uno: Cualquier número entero n divide a 0 (
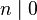 ), y 1 divide a cualquier número entero n (
), y 1 divide a cualquier número entero n (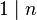 ).
).
¿Cómo calcular el número de divisores?
Para saber cuántos divisores positivos tiene un número n, primero lo descomponemos en sus factores primos. Si n es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p_{1}^{\nu _{1}}\,p_{2}^{\nu _{2}}\cdots p_{k}^{\nu _{k}} (donde 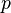 son números primos y
son números primos y 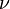 son sus exponentes), entonces el número total de divisores positivos de n se calcula multiplicando cada exponente más uno:
son sus exponentes), entonces el número total de divisores positivos de n se calcula multiplicando cada exponente más uno:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d(n)=(\nu _{1}+1)(\nu _{2}+1)\cdots (\nu _{k}+1)
Cada uno de estos divisores tendrá la forma 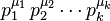 , donde cada
, donde cada 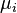 es un número entre 0 y
es un número entre 0 y 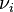 .
.
Criterios de divisibilidad: trucos para saber si un número es divisible
Estos criterios son reglas sencillas que nos permiten saber si un número es divisible entre otro sin necesidad de hacer la división completa. ¡Son muy útiles!
| Número | Criterio | Ejemplo |
|---|---|---|
| 1 | Todos los números son divisibles por 1. | 659.956.369, porque todos los números son divisibles por 1. |
| 2 | El número termina en una cifra par (0, 2, 4, 6, 8). | 378: porque la última cifra (8) es par. |
| 3 | La suma de sus cifras es un múltiplo de 3. | 480: porque 4+8+0 =12 es múltiplo de 3. |
| 4 | Sus últimos dos dígitos son 00 o un múltiplo de 4. | 300 y 516 son divisibles entre 4 porque terminan en 00 y en 16, respectivamente (16 es 4x4). |
| 5 | La última cifra es 0 o 5. | 485: porque termina en 5. |
| 6 | Es divisible entre 2 y 3 a la vez. | 912: porque es par y 9+1+2=12 (que es múltiplo de 3). |
| 7 | Separa la última cifra, multiplícala por 2 y réstala de las cifras restantes. Si el resultado es 0 o un múltiplo de 7, el número es divisible entre 7. | 34349: separamos el 9, lo duplicamos (18). Luego 3434-18=3416. Repetimos: separamos el 6, lo duplicamos (12). Luego 341-12=329. Repetimos: separamos el 9, lo duplicamos (18). Luego 32-18=14. Como 14 es múltiplo de 7, 34349 es divisible entre 7. |
| 8 | Sus tres últimas cifras son 000 o un múltiplo de 8. | 571.328: sus últimas tres cifras (328) son divisibles por 8 (328 = 8 x 41). |
| 9 | La suma de todas sus cifras es un múltiplo de 9. | 504: 5+0+4=9. Como 9 es múltiplo de 9, 504 es divisible por 9. |
| 10 | La última cifra es 0. | 4680: porque termina en 0. |
| 11 | Suma las cifras en posiciones impares por un lado y las de posiciones pares por otro. Resta ambos resultados. Si la diferencia es 0 o un múltiplo de 11, el número es divisible entre 11. | 42702: Cifras impares (4, 7, 2) suman 4+7+2=13. Cifras pares (2, 0) suman 2+0=2. La resta es 13-2=11. Como 11 es múltiplo de 11, 42702 es divisible entre 11. |
| 12 | Es divisible entre 3 y 4 a la vez. | 900: 9+0+0=9 (múltiplo de 3). Termina en 00 (múltiplo de 4). |
| 13 | Separa la última cifra, multiplícala por 9 y réstala de las cifras restantes. Si el resultado es 0 o un múltiplo de 13, el número es divisible entre 13. | 3822: separamos el 2, lo multiplicamos por 9 (18). Luego 382-18=364. Repetimos: separamos el 4, lo multiplicamos por 9 (36). Luego 36-36=0. Como el resultado es 0, 3822 es divisible entre 13. |
| 14 | Es par y divisible entre 7 a la vez. | 546: Es par. Para el 7: separamos el 6, lo duplicamos (12). Luego 54-12=42. Como 42 es múltiplo de 7, 546 es divisible entre 14. |
| 15 | Es divisible entre 3 y 5 a la vez. | 225: Termina en 5 (divisible por 5). 2+2+5=9 (múltiplo de 3). |
| 17 | Separa la última cifra, multiplícala por 5 y réstala de las cifras restantes. Si el resultado es 0 o un múltiplo de 17, el número es divisible entre 17. | 2142: separamos el 2, lo multiplicamos por 5 (10). Luego 214-10=204. Repetimos: separamos el 4, lo multiplicamos por 5 (20). Luego 20-20=0. Como el resultado es 0, 2142 es divisible entre 17. |
| 18 | Es par y divisible entre 9 a la vez. | 9702: Es par. 9+7+0+2=18 (múltiplo de 9). |
| 19 | Separa la última cifra, multiplícala por 2 y súmala a las cifras restantes. Si el resultado es múltiplo de 19, el número es divisible entre 19. | 3401: separamos el 1, lo duplicamos (2). Luego 340+2=342. Repetimos: separamos el 2, lo duplicamos (4). Luego 34+4=38. Como 38 es múltiplo de 19 (19x2), 3401 es divisible entre 19. |
| 20 | Sus dos últimas cifras son 00 o un múltiplo de 20. | 57860: Sus dos últimas cifras son 60 (que es 20x3). |
| 23 | Separa la última cifra, multiplícala por 7 y súmala a las cifras restantes. Si el resultado es múltiplo de 23, el número es divisible entre 23. | 253: separamos el 3, lo multiplicamos por 7 (21). Luego 25+21=46. Como 46 es múltiplo de 23 (23x2), 253 es divisible entre 23. |
| 25 | Sus dos últimas cifras son 00, 25, 50 o 75. | 650: Termina en 50. 400: Termina en 00. |
| 50 | Sus dos últimas cifras son 00 o 50. | 123450: Termina en 50. |
| 100 | Termina en 00. | 1000: Termina en 00. |
| 125 | Sus tres últimas cifras son 000, 125, 250, 375, 500, 625, 750 o 875. | 3000: Termina en 000. 4250: Termina en 250. |
Importante sobre los criterios
Todos estos criterios funcionan si el número está escrito en el sistema de numeración decimal (el que usamos normalmente, con base 10). Si el número está en otra base, estos criterios podrían no funcionar. Por ejemplo, el número 102 en base 7 (escrito como 1027) termina en una cifra par (2), pero no es divisible entre 2. Esto es porque en base 10, 1027 es igual a 51, que es un número impar.
Otros usos de la divisibilidad
La idea de divisibilidad no solo se aplica a los números enteros que conocemos. También se usa en otros campos de las matemáticas, como:
- Enteros gaussianos (un tipo especial de números complejos).
- Polinomios (expresiones con letras y números).
- Números de Fibonacci (una secuencia numérica especial).
Véase también
 En inglés: Divisor Facts for Kids
En inglés: Divisor Facts for Kids
- Tabla de divisores
- Máximo común divisor
- Conmensurabilidad

