Elemento simétrico para niños

En el mundo de las matemáticas, especialmente en una parte llamada Álgebra abstracta, a veces trabajamos con conjuntos de cosas y reglas para combinarlas. Imagina que tienes un grupo de objetos y una forma de "mezclarlos" o "transformarlos".

Un elemento simétrico es como el "deshacedor" de una operación. Si tienes un elemento y le aplicas una operación con su elemento simétrico, el resultado es el elemento neutro. El elemento neutro es como el "nada" o el "uno" en las operaciones, es decir, el elemento que no cambia nada cuando lo combinas con otro.

Para que exista un elemento simétrico, necesitamos tres cosas:

• Un conjunto (un grupo de elementos).
• Una operación matemática (una regla para combinar los elementos, como sumar o multiplicar).
• Un elemento neutro para esa operación.

Si tenemos un conjunto de elementos, por ejemplo, llamado A, y una operación que llamamos "círculo con un punto" (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \circledcirc ), y un elemento neutro e, entonces:

• Un elemento tiene un elemento simétrico por la izquierda si existe otro elemento que, al operarlo por la izquierda con , da como resultado el elemento neutro.
• Un elemento tiene un elemento simétrico por la derecha si existe otro elemento que, al operarlo por la derecha con , da como resultado el elemento neutro.
• Un elemento tiene un elemento simétrico (a secas) si existe un elemento que funciona como simétrico tanto por la izquierda como por la derecha. Este elemento simétrico se suele representar como .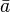

En resumen, si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \circledcirc \bar{a} = \bar{a} \circledcirc a = e , entonces 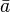es el elemento simétrico de .

Formas de escribirlo

Dependiendo de la operación que estemos usando, el elemento simétrico recibe nombres diferentes.

Cuando sumamos: el elemento opuesto

Cuando la operación es la suma (o adición), que se representa con el signo "+", al elemento simétrico lo llamamos elemento opuesto.

Ejemplo de elemento opuesto

Pensemos en el conjunto de los números enteros (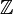), que son los números positivos, negativos y el cero (..., -2, -1, 0, 1, 2, ...). La operación es la suma.

• La suma de dos números enteros siempre da otro número entero. Por ejemplo, 3 + 5 = 8, y 8 es un número entero.
• El elemento neutro para la suma es el cero (0). Si sumas 0 a cualquier número, el número no cambia: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a + 0 = 0 + a = a . Por ejemplo, 7 + 0 = 7.
• El elemento opuesto de un número entero es 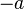. Si sumas un número con su opuesto, el resultado es el cero (el elemento neutro). Por ejemplo, el opuesto de 5 es -5, porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5 + (-5) = 0 . El opuesto de -3 es 3, porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-3) + 3 = 0 .

Cuando multiplicamos: el elemento inverso

Cuando la operación es la multiplicación (o producto), que se representa con el signo "·" o "x", al elemento simétrico lo llamamos elemento inverso.

Ejemplo de elemento inverso

Consideremos el conjunto de los números racionales (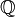), que son los números que se pueden escribir como una fracción (como 1/2, 3/4, -5/7, etc.). La operación es la multiplicación.

• La multiplicación de dos números racionales siempre da otro número racional. Por ejemplo, (1/2) · (3/4) = 3/8, y 3/8 es un número racional.
• El elemento neutro para la multiplicación es el uno (1). Si multiplicas cualquier número por 1, el número no cambia: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot 1 = 1 \cdot a = a . Por ejemplo, 9 · 1 = 9.
• El elemento inverso de un número racional (que no sea cero) es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1/a . Si multiplicas un número por su inverso, el resultado es el uno (el elemento neutro). Por ejemplo, el inverso de 5 es 1/5, porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5 \cdot (1/5) = 1 . El inverso de 2/3 es 3/2, porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (2/3) \cdot (3/2) = 1 .

Véase también

En inglés: Inverse element Facts for Kids

• Elemento neutro
• Elemento opuesto
• Elemento inverso
• Elemento absorbente
• Elemento complementario