Elipse para niños
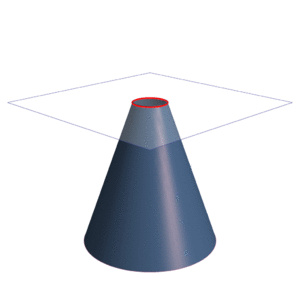
Una elipse es una forma curva, plana y cerrada que tiene dos ejes de simetría. Imagina que cortas un cono con un plano inclinado, pero sin que el corte pase por la punta del cono. La forma que obtienes es una elipse.
La elipse es especial porque todos sus puntos tienen una característica común: si sumas la distancia de cualquier punto de la elipse a otros dos puntos fijos, llamados focos, el resultado siempre es el mismo.
Si una elipse gira alrededor de su eje más corto, forma una figura parecida a una pelota aplastada. Si gira alrededor de su eje más largo, forma una figura alargada, como un balón de rugby.
Contenido
Historia de la elipse
La elipse ha sido estudiada por matemáticos desde hace mucho tiempo. Menecmo la investigó, y Euclides también la estudió. El nombre "elipse" se le atribuye a Apolonio de Pérgamo.
En el año 1602, el astrónomo Johannes Kepler pensó que la órbita del planeta Marte era ovalada. Más tarde, descubrió que en realidad era una elipse, y que el Sol estaba en uno de sus focos (uno de esos puntos fijos especiales). Kepler fue quien introdujo la palabra "foco" en este contexto.
En 1705, Edmond Halley demostró que el cometa que lleva su nombre también se mueve en una órbita elíptica alrededor del Sol.
Partes de una elipse
Una elipse es una curva plana y cerrada. Es simétrica, lo que significa que puedes dividirla en dos partes iguales con dos líneas que se cruzan. Estas líneas son sus ejes:
- El semieje mayor es la mitad de la distancia más larga a través de la elipse.
- El semieje menor es la mitad de la distancia más corta a través de la elipse.
Focos de una elipse
Los focos de la elipse son dos puntos fijos, llamados F1 y F2, que están en el eje mayor. Son muy importantes porque, como ya dijimos, la suma de las distancias desde cualquier punto de la elipse a estos dos focos siempre es la misma. Esta suma es igual a la longitud del eje mayor.
Ejes de una elipse
El eje mayor es la distancia más grande entre dos puntos opuestos de la elipse. Se representa como 2a. El eje menor es la distancia más pequeña entre dos puntos opuestos de la elipse. Se representa como 2b. Los dos ejes de la elipse siempre se cruzan formando un ángulo recto (90 grados).
Excentricidad de una elipse
La excentricidad (se escribe con la letra griega épsilon, ε) de una elipse nos dice qué tan "aplastada" o "redonda" es.
Se calcula dividiendo la distancia del centro al foco (llamada 'c') entre la longitud del semieje mayor ('a'). Su valor siempre está entre 0 y 1.
- Si la excentricidad es cercana a 0, la elipse es casi un círculo.
- Si la excentricidad es cercana a 1, la elipse es muy alargada o "aplastada".
Constante de la elipse
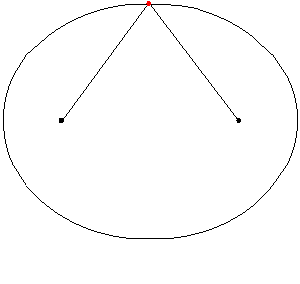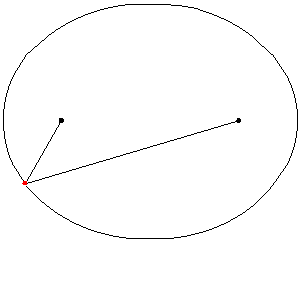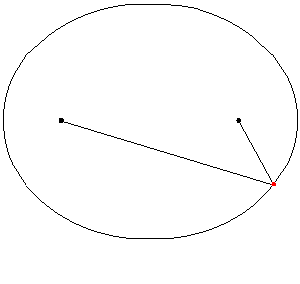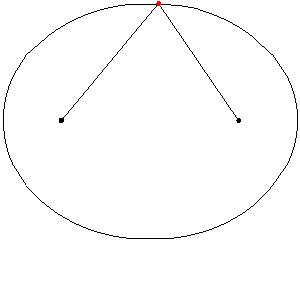
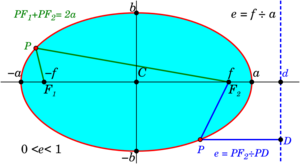
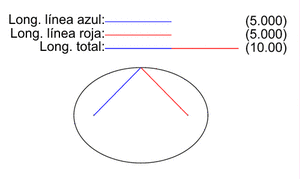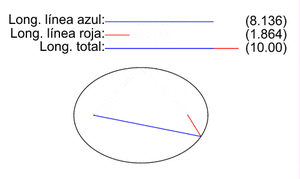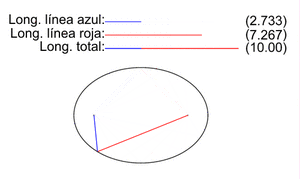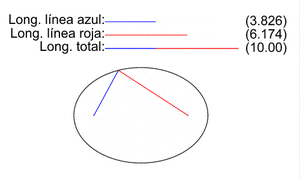
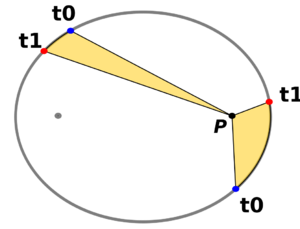
Para cualquier punto P en la elipse, si mides la distancia desde P hasta el foco F1 (PF1) y la distancia desde P hasta el foco F2 (PF2), y luego sumas esas dos distancias, el resultado siempre será el mismo. Esta suma constante es igual a la longitud del eje mayor (2a).
Por ejemplo, en la imagen, si el eje mayor mide 10, la suma de PF1 + PF2 siempre será 10 para cualquier punto de la elipse.
Directrices de la elipse
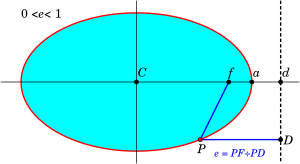
Cada foco de la elipse tiene asociada una línea recta especial llamada directriz. Esta línea es paralela al semieje menor.
Hay una propiedad interesante: si tomas cualquier punto P de la elipse, la distancia de P al foco F, dividida por la distancia de P a la directriz, siempre da como resultado la excentricidad de la elipse. Esta es otra forma de definir una elipse.
Cómo dibujar una elipse
La elipse "del jardinero"
Este es un método sencillo para dibujar elipses, incluso grandes, usando solo una cuerda y dos puntos fijos. Se llama "del jardinero" porque es útil para trazar elipses en el suelo.
1. Coloca dos clavos o chinchetas en el lugar donde quieres que estén los focos de la elipse. 2. Toma una cuerda cuya longitud sea igual al eje mayor de la elipse que quieres dibujar. 3. Ata los extremos de la cuerda a los dos clavos. 4. Con un lápiz, estira la cuerda y muévelo alrededor de los clavos, manteniendo la cuerda tensa en todo momento. El lápiz dibujará la elipse perfecta.
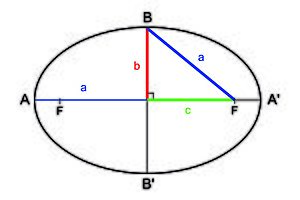
Cómo encontrar los focos
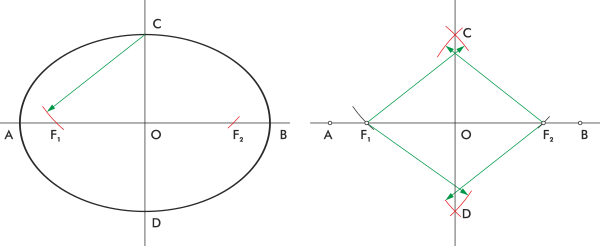
Si ya tienes los dos ejes de la elipse dibujados, puedes encontrar los focos así:
1. Toma un compás y abrelo con la medida del semieje mayor (la mitad del eje más largo). 2. Coloca la punta del compás en uno de los extremos del eje menor (el eje más corto). 3. Dibuja un arco que cruce el eje mayor. Los dos puntos donde el arco cruza el eje mayor son los focos de la elipse.
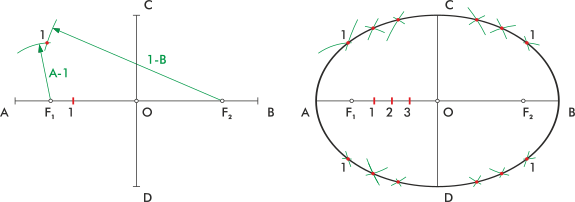
Método de radios vectores
Este método te permite dibujar una elipse marcando varios puntos.
1. Dibuja los ejes principales y encuentra los focos. 2. Elige algunos puntos al azar sobre el eje mayor, entre el centro y uno de los focos. 3. Con el compás, mide la distancia desde un extremo del eje mayor (A) hasta uno de esos puntos que elegiste (punto 1). 4. Con esa medida, y haciendo centro en cada foco, traza dos arcos. 5. Ahora, mide la distancia desde el punto 1 hasta el otro extremo del eje mayor (B). 6. Con esta nueva medida, y haciendo centro de nuevo en los focos, cruza los arcos que trazaste antes. Los puntos donde se cruzan los arcos son puntos de la elipse. 7. Repite este proceso con otros puntos del eje mayor para obtener más puntos de la elipse. 8. Finalmente, une todos los puntos a mano o con una plantilla de curvas para completar la elipse.
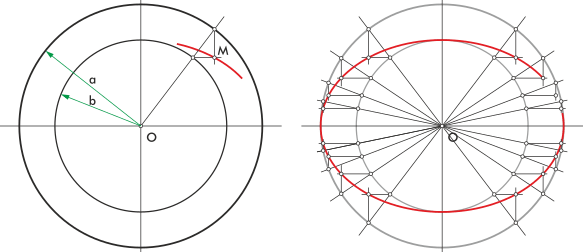
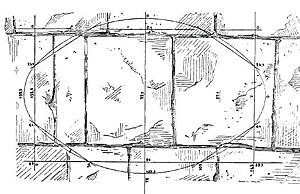
Construcción por afinidad
Este método usa dos círculos concéntricos (con el mismo centro) para dibujar la elipse.
1. Dibuja dos círculos con el mismo centro que la elipse, uno con el diámetro del eje mayor y otro con el diámetro del eje menor. 2. Desde el centro, traza una línea recta (un radio) que cruce ambos círculos. 3. Desde el punto donde el radio corta el círculo más grande, traza una línea auxiliar paralela al eje menor, hacia el centro. 4. Desde el punto donde el radio corta el círculo más pequeño, traza una línea auxiliar paralela al eje mayor. 5. El punto donde se cruzan estas dos líneas auxiliares es un punto de la elipse. 6. Repite este proceso varias veces para obtener suficientes puntos y luego únelos para formar la elipse.
Ecuaciones de la elipse
Las ecuaciones son fórmulas matemáticas que describen la forma de la elipse en un plano.
En coordenadas cartesianas
- Elipse centrada en el origen (0,0):
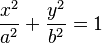 Aquí, 'a' es la longitud del semieje mayor y 'b' es la longitud del semieje menor.
Aquí, 'a' es la longitud del semieje mayor y 'b' es la longitud del semieje menor.
- Elipse centrada fuera del origen (h,k):
Si el centro de la elipse no está en (0,0) sino en un punto (h,k), la ecuación cambia un poco: 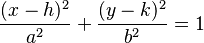
Área de la elipse
El área de la región que encierra una elipse se calcula con una fórmula sencilla:
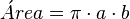
Donde 'a' es el semieje mayor y 'b' es el semieje menor.
Perímetro de una elipse
Calcular el perímetro (la longitud del borde) de una elipse es más complicado que calcular su área. No hay una fórmula sencilla y exacta como la del círculo. Sin embargo, el matemático Srinivasa Ramanujan encontró una fórmula que se acerca mucho al valor real:
![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](/images/math/4/5/3/4531867e543bc27be7c45f80a7599da1.png)
La elipse como figura cónica
La elipse es una de las figuras que se obtienen al cortar un cono con un plano. Por eso, a la elipse, la parábola, la hipérbola y el círculo se les llama secciones cónicas o simplemente cónicas.
La elipse en el espacio
En el espacio, los planetas y otros cuerpos celestes se mueven en órbitas que son elipses. Esto lo descubrió Johannes Kepler con sus leyes de Kepler.
La segunda ley de Kepler dice que un planeta se mueve más rápido cuando está más cerca del Sol y más lento cuando está más lejos. Pero lo hace de tal manera que, en el mismo tiempo, el área que "barre" su línea imaginaria al Sol es siempre la misma. Esto significa que las áreas amarillas en el diagrama son iguales, aunque los arcos recorridos sean diferentes. El Sol está en uno de los focos de la elipse.
La elipse en la vida diaria
Las elipses aparecen en muchos lugares de nuestra vida cotidiana:
- Si inclinas un vaso de agua cilíndrico, la superficie del agua forma una elipse.
- En algunas estaciones de metro o edificios con forma elíptica, si te paras en un foco y otra persona en el otro foco, pueden escucharse muy bien, incluso si están lejos. Esto se debe a una propiedad de la elipse: las ondas de sonido que salen de un foco rebotan en las paredes y se dirigen hacia el otro foco.
Ver también
Véase también
 En inglés: Ellipse Facts for Kids
En inglés: Ellipse Facts for Kids