Elipsógrafo para niños
Un elipsógrafo es una herramienta mecánica que sirve para dibujar elipses de forma continua. Imagina que quieres dibujar una forma ovalada perfecta; un elipsógrafo te ayuda a hacerlo con precisión.
Además de métodos muy sencillos, como usar una cuerda y dos puntos fijos (conocido como el método del jardinero), existen elipsógrafos más complejos. Algunos son sistemas con piezas que se mueven en un plano, llamados trameles, y otros son sistemas tridimensionales, como los compases perfectos. Muchos matemáticos famosos han creado sus propios elipsógrafos, basándose en las propiedades especiales de las elipses.
Algunos diseños de elipsógrafos, como el mecanismo de Arquímedes, no solo sirven para dibujar, sino también para cortar o dar forma a elipses en materiales como la madera. Esto se logra al unir una cuchilla o una herramienta de corte a la varilla del elipsógrafo. Generalmente, puedes ajustar las distancias en el instrumento para cambiar el tamaño y la forma de la elipse que quieres crear.
Elipsógrafo: La Máquina para Dibujar Elipses
¿Qué es un Elipsógrafo?
Un elipsógrafo es un instrumento diseñado para trazar elipses de manera precisa y continua. Una elipse es una figura geométrica que parece un círculo estirado, como un óvalo. Piensa en la órbita de los planetas alrededor del Sol, que son elipses. Estas herramientas son muy útiles en ingeniería, diseño y matemáticas.
El Elipsógrafo de Arquímedes: Un Clásico
Aunque se le atribuye a Arquímedes, algunos historiadores creen que este elipsógrafo podría haber sido descrito por el geómetra griego Proclo. Se sabe que el Marqués de L'Hôpital construyó uno en 1707.
¿Cómo Funciona el Elipsógrafo de Arquímedes?
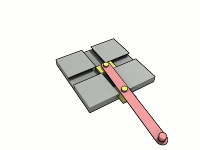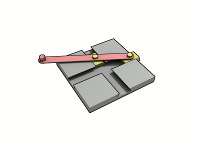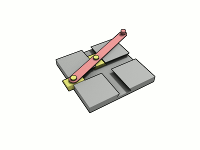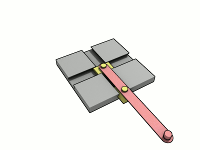
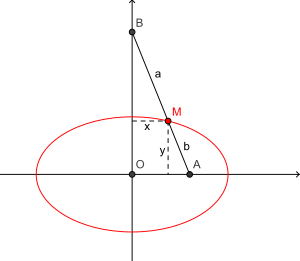
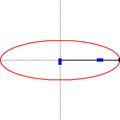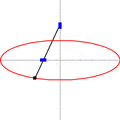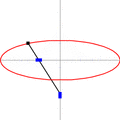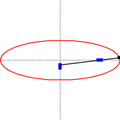
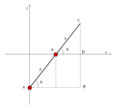
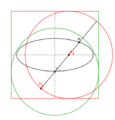
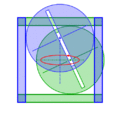
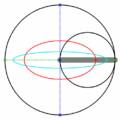
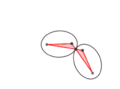
Este elipsógrafo funciona con una barra que tiene dos puntos (llamados "lanzaderas") que se deslizan en dos canales o rieles que están en ángulo recto (perpendiculares) entre sí. Un lápiz o punta de dibujo se coloca en otro punto de la barra. A medida que las lanzaderas se mueven por los canales, el lápiz dibuja una elipse.
La forma de la elipse depende de la distancia entre el lápiz y cada una de las lanzaderas. Si la distancia es la misma, se dibuja un círculo, que es un tipo especial de elipse. Este movimiento de la barra se llama movimiento elíptico.
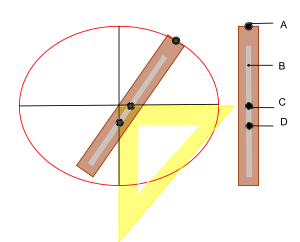
Una versión sencilla de este elipsógrafo fue ideada por Gastón Tissandier. Solo necesitas una escuadra y una regla con una ranura. Colocas dos tornillos deslizantes en la regla y los ajustas a ciertas distancias. Luego, giras la regla manteniendo los tornillos en contacto con los lados de la escuadra, y una punta en la regla dibujará la elipse.
Sin embargo, los elipsógrafos de Arquímedes pueden tener algunos inconvenientes:
- Las piezas deslizantes pueden causar imprecisiones, haciendo que el dibujo no sea perfecto.
- El sistema de guía puede dificultar el dibujo de elipses muy estrechas o incluso bloquear el lápiz.
Para solucionar esto, se han creado elipsógrafos donde los puntos deslizantes se guían de forma indirecta, usando círculos que se mueven dentro de un marco.
Otros Elipsógrafos Famosos
Elipsógrafos de Van Schooten
Frans van Schooten, un matemático holandés del siglo XVII, escribió un libro completo sobre cómo construir formas cónicas, incluyendo elipses. Él mejoró el principio del elipsógrafo de Arquímedes y también inventó otros dos mecanismos.
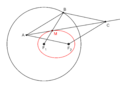
Uno de sus elipsógrafos funciona con una barra de cierta longitud. Si un punto de la barra se mueve sobre un eje y otro punto sobre un eje perpendicular, un tercer punto en la barra dibujará una elipse.
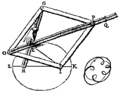
También creó un elipsógrafo usando un "antiparalelogramo", que es una figura con cuatro lados donde los lados opuestos se cruzan y tienen la misma longitud. Al fijar dos puntos de esta figura en los focos de la elipse (los puntos clave que definen una elipse), y mover las otras partes, un punto de intersección de las barras dibuja la elipse.
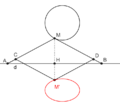
Otro de sus diseños usa un rombo (una figura de cuatro lados iguales) con una varilla deslizante. Al fijar dos puntos en los focos de la elipse y mover la varilla, un punto de intersección dibuja la elipse. Este instrumento también puede mostrar la línea tangente a la elipse en cada punto.
Elipsógrafos Multifuncionales
Algunos matemáticos han buscado crear instrumentos que no solo dibujen elipses, sino también otras formas geométricas. Por ejemplo, en 1818, Joseph Clement construyó un aparato que podía dibujar círculos, líneas paralelas y espirales, además de elipses.
También existen elipsógrafos que son polígonos articulados (figuras con varios lados unidos por bisagras) que pueden realizar varias funciones. Un ejemplo es el elipsógrafo de Darboux y Breguet de 1879, que es un pentágono articulado capaz de dibujar líneas perpendiculares, elipses y otras curvas llamadas "caracoles de Pascal".
El Compás Cónico: Otra Forma de Dibujar Elipses
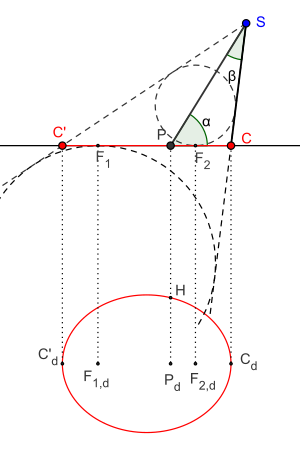
También puedes dibujar una elipse usando un compás cónico. Este compás tiene un brazo de longitud fija y otro de longitud variable. La punta de dibujo siempre se mantiene en contacto con la superficie. Un eje del compás mantiene una dirección constante y un ángulo fijo. Cuando el brazo variable gira alrededor del eje fijo, la punta de dibujo traza una elipse.
Los primeros compases cónicos, llamados "compases perfectos", fueron estudiados por matemáticos árabes desde el siglo X. En Europa, aparecieron durante el Renacimiento con figuras como Alberto Durero y Leonardo da Vinci, cuando el dibujo en perspectiva se hizo popular.
La ventaja de un compás cónico sobre un sistema articulado es que permite variar los parámetros de la elipse de forma continua, lo que da más flexibilidad.
El Elipsógrafo de Arquímedes como Juguete
El mecanismo de Arquímedes, conocido en inglés como trammel, también se ha convertido en un juguete popular. Consiste en dos piezas que se deslizan en canales perpendiculares y una varilla unida a ellas.
Las versiones de madera de este mecanismo se han vendido como juguetes con nombres curiosos como Kentucky do-nothings, nothing grinders o bullshit grinders. En estos juguetes, la parte que dibuja se reemplaza por una manivela, y las posiciones de las piezas deslizantes suelen ser fijas.
Además, se han creado versiones modernas de este mecanismo en juguetes de construcción como el Lego, permitiendo a los niños construir y entender cómo funcionan estas interesantes máquinas.
Galería de imágenes
-
Mecanismo de Arquímedes
-
Diagrama
-
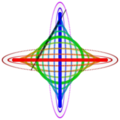
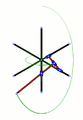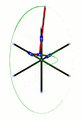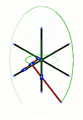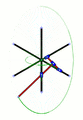
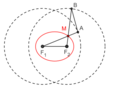
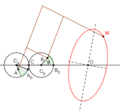
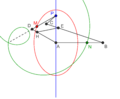
Lugares geométricos de algunos puntos a lo largo y más allá de un mecanismo de Arquímedes. En verde, el círculo descrito por el punto medio – en el fichero SVG, mover el puntero sobre el diagrama para mover el mecanismo
-
Mecanismo de Arquímedes con tres lanzaderas
-
Principio del círculo elipsográfico de Rohn
-
Círculo elipsográfico de Rohn (realización)
-
Principio de La Hire
-
Elipsógrafo - Deutsches Museum
-
Principio del elipsógrafo con un antiparalelogramo
-
Elipsógrafo con un antiparalelogramo (animación)
-
Elipsógrafo de van Schooten (1646)
-
Principio del elipsógrafo con un círculo directriz
-
Principio del elipsógrafo de Delaunay
-
Principio del elipsógrafo de Kopp (1993)
-
Elipsógrafo de Darboux Breguet
Véase también
- Compás radial
- Máquina de Bourke
- John Farey Jr.
- Hipocicloide
- Hipotrocoide
- Acople Tusi
- Máquina sin uso
