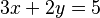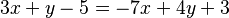Ecuación de primer grado para niños
Una ecuación de primer grado o ecuación lineal es un tipo de ecuación algebraica donde las variables (o incógnitas) solo aparecen sumando o restando, y no tienen exponentes (es decir, están elevadas a la primera potencia). Son muy importantes en la escuela secundaria.
En matemáticas, una ecuación lineal se puede escribir así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1x_1+\ldots+a_nx_n+b=0, Aquí,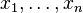 
son las variables (los valores que queremos encontrar). Los símbolos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b,a_1,\ldots,a_n son los coeficientes, que suelen ser números reales. Para que la ecuación tenga sentido, al menos uno de los coeficientes Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1, \ldots, a_n no debe ser cero.
La solución de una ecuación son los valores que, al ponerlos en lugar de las incógnitas, hacen que la igualdad sea verdadera.
Las ecuaciones lineales aparecen mucho en matemáticas, física e ingeniería. Esto es porque muchos problemas complejos se pueden simplificar y entender mejor usando ecuaciones lineales.
Contenido
¿Qué es una Ecuación de Primer Grado?
Una ecuación de primer grado es una igualdad matemática que tiene una o más variables. La característica principal es que estas variables no están elevadas a ninguna potencia mayor que uno. Por ejemplo, no verás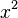 
o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y^3 .
Ecuaciones con una Sola Incógnita
Cuando una ecuación de primer grado tiene solo una variable, como la letra 'x', generalmente tiene una única solución. A menudo, cuando se habla de "ecuación lineal", se refieren a este tipo.
En muchos países, estas ecuaciones se estudian al principio de la educación secundaria. Ayudan a los estudiantes a aprender cómo usar el álgebra para resolver problemas.
¿Cómo se ve una Ecuación de Primer Grado con una Variable?
Una ecuación de primer grado con una sola variable se ve así:
|
Aquí, 'x' es la variable que queremos encontrar. 'a' y 'b' son números conocidos. La 'a' no puede ser cero.
¿Cómo se Resuelve?
Para encontrar el valor de 'x', se usa esta fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = - \frac{b}{a}
La solución de una ecuación lineal con una variable se puede representar en una gráfica como un punto en una recta numérica.
Ecuaciones con Dos Incógnitas
Cuando una ecuación lineal tiene dos variables, como 'x' e 'y', nos permite entender cómo se relacionan estas dos cantidades. En la escuela, se usan para resolver problemas de la vida real.
Forma Común de Ecuaciones con Dos Variables
Una forma muy usada para escribir ecuaciones lineales con dos variables es:
;
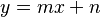Esta forma se llama "explícita".
Aquí, 'm' representa la pendiente de la recta (qué tan inclinada está). El valor de 'n' nos dice dónde la recta corta el eje Y (se llama "ordenada al origen").
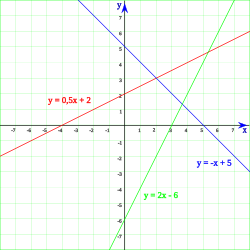
Representación Gráfica
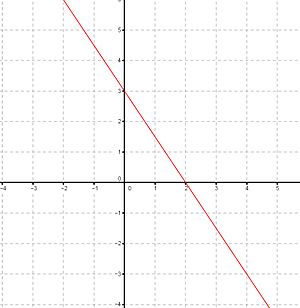
En un sistema de coordenadas cartesianas, las ecuaciones lineales con dos incógnitas siempre representan rectas. Por eso se les llama "lineales". Cada punto en la recta es una solución de la ecuación.
Algunos ejemplos de ecuaciones lineales con dos incógnitas son:
A veces, necesitas usar reglas de álgebra para ponerlas en la forma explícita (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = mx + n ).
Otras Formas de Escribir Ecuaciones Lineales
Las ecuaciones lineales pueden escribirse de diferentes maneras. Las letras mayúsculas (A, B, C, E, F, U, V) representan números fijos, mientras que 'x' e 'y' son las variables.
- Ecuación general
:: 
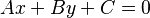: En esta forma, 'A' y 'B' no pueden ser cero al mismo tiempo. También representa una línea en el plano cartesiano.
- Ecuación segmentaria o simétrica
:: 
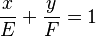: Aquí, 'E' y 'F' no pueden ser cero. La gráfica de esta ecuación corta el eje X en 'E' y el eje Y en 'F'.
- Forma paramétrica
# 
# 
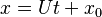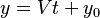: Son dos ecuaciones que deben cumplirse al mismo tiempo, usando una nueva variable 't'. Esta forma nos dice que la recta pasa por el punto 
.
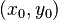- Casos especiales:
* 
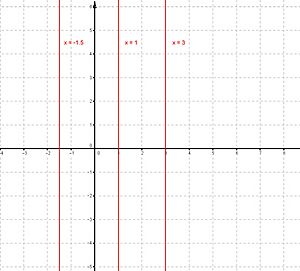
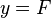: Esta es una línea horizontal. Si F es 0, la línea está sobre el eje X. * 
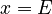: Esta es una línea vertical. Corta el eje X en 'E'. * 
: Si al simplificar una ecuación llegas a esto, significa que la ecuación es siempre verdadera. Su gráfica es todo el plano cartesiano.
Si al simplificar una ecuación llegas a algo como 1 = 0, significa que la ecuación no tiene solución. Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 x + 2 =3 x .
Ecuaciones Lineales en el Espacio Tridimensional
Las ecuaciones lineales también tienen un significado geométrico en espacios con más dimensiones.
Ecuaciones con Tres o Más Incógnitas
Cuando tenemos una ecuación lineal con tres variables, como 'x', 'y' y 'z', su solución representa un plano en el espacio tridimensional.
En general, una ecuación lineal con 'n' variables representa un "hiperplano" en un espacio de 'n' dimensiones. Un hiperplano es como una versión de un plano, pero en más dimensiones.
¿Cómo se ve una Ecuación con Más de Dos Variables?
Siempre podemos escribir una ecuación lineal con muchas variables de esta forma:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1 x_1 + a_2 x_2 + \cdots + a_n x_n + b=0.
Aquí,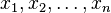 
son las variables. El número 'b' se llama "término constante".
Una solución para este tipo de ecuación es un conjunto de valores (una "n-tupla") que, al sustituirlos por las variables, hacen que la ecuación sea verdadera.
Sistemas de Ecuaciones Lineales
Un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones lineales que se deben resolver al mismo tiempo. Buscamos los valores de las variables que satisfacen todas las ecuaciones a la vez.
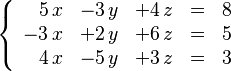
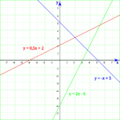
Geométricamente, resolver un sistema de ecuaciones lineales es encontrar el punto (o puntos) donde todas las líneas o planos se cruzan.
- Para dos ecuaciones con dos incógnitas, la solución es el punto donde se cruzan dos líneas.
- Para tres ecuaciones con tres incógnitas, la solución es el punto donde se cruzan tres planos.
Aplicaciones de las Ecuaciones Lineales
Las ecuaciones lineales son muy importantes en matemáticas y en la vida real por varias razones:
- Son las ecuaciones más sencillas de entender y resolver. Por eso, son perfectas para enseñar cómo plantear y solucionar problemas matemáticos.
- Muchos fenómenos de la física y la ingeniería se pueden describir con leyes lineales (o proporcionales). Una ecuación lineal es la forma de expresar un problema que sigue una de estas leyes.
- Incluso fenómenos más complejos pueden simplificarse y aproximarse usando ecuaciones lineales, lo que facilita su estudio.
Galería de imágenes
-
Ejemplo: ecuación de una variable
-
Ejemplo gráfico de ecuaciones lineales.
-
Ejemplo de forma segmentaria: x/2 + y/3 = 1
-
La solución de una ecuación lineal real con tres incógnitas es generalmente un plano.
Véase también
- Función lineal
- Ecuación algebraica
- Coordenadas de la recta
- Desigualdad lineal
- Sistema no lineal
- Ecuación de segundo grado
- Ecuación diferencial lineal
