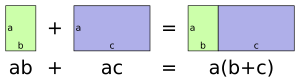
Distributividad para niños
En matemáticas, la propiedad distributiva es una regla muy útil que nos ayuda a resolver operaciones. Imagina que tienes un número y lo quieres multiplicar por una suma de otros números. Esta propiedad dice que puedes multiplicar ese número por cada parte de la suma por separado y luego sumar los resultados. ¡El resultado final será el mismo!
En álgebra (que es como la aritmética, pero con letras y símbolos), se ve así:
Esto significa que si tienes un número a y lo multiplicas por la suma de b y c, es lo mismo que si multiplicas a por b y luego a por c, y al final sumas esos dos resultados.
Veamos un ejemplo con números: Si queremos calcular Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \cdot (5 + 4) : Primero, sumamos lo que está dentro del paréntesis: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \cdot (9) = 27
Ahora, usando la propiedad distributiva, multiplicamos el 3 por cada número dentro del paréntesis y luego sumamos: 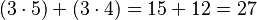
Como puedes ver, ¡el resultado es el mismo en ambos casos! Esta propiedad es fundamental y se usa en muchas áreas de las matemáticas, como con los números complejos, los polinomios y las matrices.
Contenido
¿Qué es la propiedad distributiva?
La propiedad distributiva es una regla que conecta dos operaciones matemáticas, como la multiplicación y la suma. Nos dice cómo se comporta una operación cuando se combina con otra.
Distributividad por la izquierda y por la derecha
A veces, la propiedad distributiva puede funcionar de dos maneras:
- Por la izquierda: Cuando el número que multiplica está a la izquierda del paréntesis. Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot (b + c) = (a \cdot b) + (a \cdot c)
- Por la derecha: Cuando el número que multiplica está a la derecha del paréntesis. Por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (b + c) \cdot a = (b \cdot a) + (c \cdot a)
Si una operación cumple ambas, decimos que es simplemente "distributiva". En la multiplicación normal, como la que usamos con los números, no importa si multiplicamos por la izquierda o por la derecha, el resultado es el mismo.
Ejemplos de la propiedad distributiva
La propiedad distributiva es muy útil en la vida diaria y en problemas de matemáticas.
Números reales
Los números reales son los números que usamos normalmente (enteros, decimales, fracciones). La propiedad distributiva funciona perfectamente con ellos.
- Primer ejemplo (cálculo mental)
A veces usamos la distributividad sin darnos cuenta cuando hacemos cálculos mentales: Para calcular 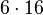 : Podemos pensar en 16 como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10 + 6 . Entonces, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6 \cdot 16 = 6 \cdot (10 + 6) Aplicando la propiedad distributiva: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6 \cdot 10 + 6 \cdot 6 = 60 + 36 = 96 ¡Así es más fácil calcularlo!
: Podemos pensar en 16 como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10 + 6 . Entonces, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6 \cdot 16 = 6 \cdot (10 + 6) Aplicando la propiedad distributiva: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6 \cdot 10 + 6 \cdot 6 = 60 + 36 = 96 ¡Así es más fácil calcularlo!
- Segundo ejemplo (con letras o variables)
La propiedad distributiva también se usa mucho en álgebra con letras que representan números (variables): 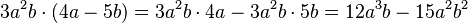 Aquí, el término Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 a^2 b se multiplica por cada parte dentro del paréntesis.
Aquí, el término Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 a^2 b se multiplica por cada parte dentro del paréntesis.
- Tercer ejemplo (multiplicar dos sumas)
Cuando multiplicamos dos paréntesis, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a + b) \cdot (c + d) , también usamos la propiedad distributiva varias veces. Multiplicamos cada término del primer paréntesis por cada término del segundo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle (a + b) \cdot (c + d) = a \cdot c + a \cdot d + b \cdot c + b \cdot d} Por ejemplo, para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a + b) \cdot (a - b) : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle \begin{align} (a + b) \cdot (a - b) & = a \cdot (a - b) + b \cdot (a - b) \\ & = a^2 - ab + ba - b^2 \\ & = a^2 - b^2 \\ \end{align}} Este es un caso especial que se usa mucho en álgebra.
- Cuarto ejemplo (sacar factor común)
La propiedad distributiva también funciona al revés. Si tienes una suma donde todos los términos tienen un factor en común, puedes "sacar" ese factor. Esto se llama sacar factor común: Imagina que tienes: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 12 a^3 b^2 - 30 a^4 b c + 18 a^2 b^3 c^2 Puedes ver que 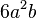 está en todos los términos. Entonces, lo sacamos:
está en todos los términos. Entonces, lo sacamos: 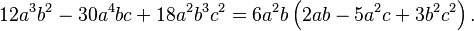 Esto simplifica la expresión.
Esto simplifica la expresión.
Matrices
Las matrices son arreglos de números en filas y columnas. La multiplicación de matrices también cumple la propiedad distributiva: 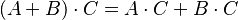 y
y 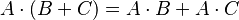 Aquí, A, B y C son matrices.
Aquí, A, B y C son matrices.
Otros ejemplos
La propiedad distributiva aparece en muchas otras áreas de las matemáticas:
- La unión de conjuntos es distributiva con respecto a la intersección, y viceversa.
- En lógica matemática, la disyunción lógica ("o") es distributiva sobre la conjunción lógica ("y"), y viceversa.
- Para los números reales, la operación de encontrar el número más grande (máximo) es distributiva sobre la operación de encontrar el número más pequeño (mínimo), y viceversa.
- Para los enteros, el máximo común divisor (MCD) es distributivo con respecto al mínimo común múltiplo (mcm), y viceversa.
Distributividad y redondeo
Cuando trabajamos con números decimales muy largos o en computadoras, a veces la propiedad distributiva puede parecer que no funciona perfectamente. Esto se debe a que las computadoras tienen un límite en la precisión con la que guardan los números. Por ejemplo, 1/3 no se puede escribir exactamente como un decimal finito (es 0.333...). Si sumamos 1/3 + 1/3 + 1/3, el resultado debería ser 1. Pero si usamos 0.333, la suma sería 0.999, que no es exactamente 1. Estos pequeños errores son normales en la aritmética de computadora.
Lógica proposicional
En lógica proposicional, que estudia cómo se conectan las frases (proposiciones) con "y", "o", "si... entonces", etc., también existen reglas de distributividad. Estas reglas nos permiten cambiar la forma de una expresión lógica sin alterar su significado. Por ejemplo:
- Si tienes "P y (Q o R)", es lo mismo que "(P y Q) o (P y R)".
- Si tienes "P o (Q y R)", es lo mismo que "(P o Q) y (P o R)".
Generalizaciones
La idea de distributividad es tan importante que los matemáticos la han extendido a muchas otras áreas y estructuras más complejas. A veces, las reglas son un poco diferentes o más específicas, pero la idea principal de "distribuir" una operación sobre otra se mantiene.
Antidistributividad
En algunos casos especiales, existe una propiedad que es lo contrario a la distributividad, llamada "antidistributividad". Por ejemplo, en los grupos (que son conjuntos con una operación que cumple ciertas reglas), la inversa de un producto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x \cdot y)^{-1} es igual al producto de las inversas en orden inverso: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y^{-1} \cdot x^{-1} . Esto es un ejemplo de antidistributividad.
Véase también
 En inglés: Distributive property Facts for Kids
En inglés: Distributive property Facts for Kids
Galería de imágenes