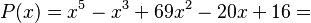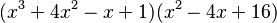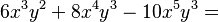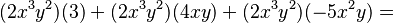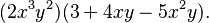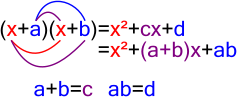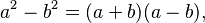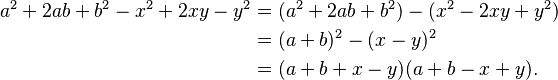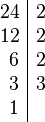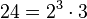Factorización para niños

Enciclopedia para niños

La factorización en matemáticas es una técnica para transformar una expresión grande (como un número o un polinomio) en una multiplicación de partes más pequeñas, llamadas factores. Imagina que tienes un número como el 12. Puedes escribirlo como 3 x 4. Aquí, 3 y 4 son los factores de 12. El objetivo principal de la factorización es simplificar las expresiones o reescribirlas en sus "bloques de construcción" más básicos.

Por ejemplo, un número se puede descomponer en números primos (como 12 = 2 x 2 x 3), y un polinomio se puede descomponer en polinomios más simples que no se pueden factorizar más.

Lo contrario de la factorización es la expansión, que es cuando multiplicas los factores para obtener la expresión original.

El teorema fundamental de la aritmética nos dice que cada número entero positivo tiene una forma única de descomponerse en factores primos. Para los polinomios, existe un teorema similar llamado teorema fundamental del álgebra.

Factorización de números enteros

Según el teorema fundamental de la aritmética, cualquier número entero positivo se puede escribir de una única manera como una multiplicación de números primos. Estos números primos son los "ladrillos" básicos de los números. Por ejemplo, el número 30 se puede escribir como 2 x 3 x 5.

Factorización de polinomios

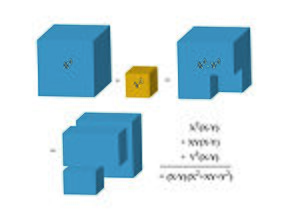
La factorización de polinomios es una técnica para descomponer una expresión matemática en forma de multiplicación. Cuando factorizamos polinomios, buscamos que los factores sean polinomios de un grado más pequeño. Por ejemplo, si tenemos un polinomio como x² - 4, podemos factorizarlo como (x - 2) (x + 2). Aquí, (x - 2) y (x + 2) son los factores.

A veces, un polinomio no se puede factorizar más usando ciertos tipos de números. Por ejemplo, x² + 4 no se puede factorizar usando solo números reales.

Un polinomio de grado n (el grado es el exponente más alto de la variable) se puede factorizar en un producto de polinomios de grados más pequeños. Por ejemplo, un polinomio de grado 5 se puede factorizar como el producto de un polinomio de grado 3 y uno de grado 2:

P(x) = x^5-x^3+69x^2-20x+16 =

(x^3+4x^2-x+1)(x^2-4x+16)

¿Para qué se usa la factorización de polinomios?

La factorización de polinomios es muy útil en matemáticas para:

Resolver ecuaciones: Ayuda a encontrar los valores de x que hacen que una ecuación sea verdadera.
Sumar y restar fracciones: Facilita la operación con fracciones que tienen polinomios.
Simplificar expresiones: Hace que las expresiones complicadas sean más fáciles de entender y trabajar.

Historia de la factorización

Aunque hoy en día la factorización es un método muy importante para resolver ecuaciones cuadráticas (ecuaciones con x²), no siempre fue así. Vera Sanford menciona en su libro A Short History of Mathematics (1930) que este método no se usó mucho hasta el trabajo de Thomas Harriot en 1631. Harriot fue un matemático que murió en 1621, y sus libros se publicaron después de su muerte.

Harriot usaba tablas para mostrar cómo se multiplicaban expresiones con uno, dos o tres términos. Luego, mostraba cómo esa multiplicación era la base para su método de factorización. Él escribía formas para diferentes multiplicaciones, como (a ± b) (a ± c), y luego, al ver una expresión, la ajustaba a una de esas formas para encontrar sus factores.

Métodos comunes de factorización

Existen varios métodos para factorizar polinomios. Aquí te presentamos algunos de los más usados:

Factor común

Este método consiste en encontrar un término (un número, una letra o ambos) que se repita en todos los términos del polinomio. Es como sacar lo que tienen en común. Por ejemplo:

6x^3y^2 + 8x^4y^3 - 10x^5y^3 =

(2x^3y^2)(3) + (2x^3y^2)(4xy) + (2x^3y^2)(-5x^2y) =

(2x^3y^2)(3 + 4xy -5x^2y).

Aquí, el factor común es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2x^3y^2 .

Factor común por agrupación de términos

A veces, no hay un factor común en todos los términos, pero sí en grupos de términos. Este método consiste en agrupar los términos y luego factorizar cada grupo. Si tienes suerte, los resultados de esas factorizaciones parciales se pueden combinar.

Por ejemplo, para factorizar el polinomio:

4x^2+20x+3xy+15y \,

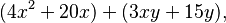
Agrupamos los términos: $(4x^2+20x)+(3xy+15y),\,$
Factorizamos el factor común en cada grupo: $4x(x+5)+3y(x+5),\,$
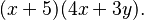
Ahora, (x+5) es un factor común en ambos grupos, así que lo factorizamos de nuevo: $(x+5)(4x+3y).\,$

Teorema del factor

Para un polinomio p(x), el teorema del factor dice que si un número a hace que p(a) sea igual a 0 (es decir, a es una "raíz" o "cero" del polinomio), entonces (x - a) es un factor de p(x). Puedes encontrar el otro factor usando la división polinómica.

Por ejemplo, si tenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^3 - 3x + 2 , y probamos con x = 1, vemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1^3 - 3(1) + 2 = 1 - 3 + 2 = 0 . Entonces, (x - 1) es un factor. Al dividir Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^3 - 3x + 2 entre (x - 1), obtenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + x - 2 . Así, 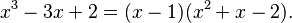$x^3 - 3x + 2 = (x - 1)(x^2 + x - 2).$

Reconocimiento de patrones

A menudo, la factorización se basa en reconocer ciertos patrones en la expresión. Aquí hay algunos patrones comunes:

Diferencia de dos cuadrados

El polinomio x² + cx + d, donde a + b = c y ab = d, puede ser factorizado en (x + a)(x + b).

Este es un patrón muy común: la resta de dos términos que son cuadrados perfectos. La fórmula es:

a^2 - b^2 = (a+b)(a-b),\,\!

Por ejemplo, x² - 9 = (x + 3) (x - 3).

A veces, las expresiones son más complejas, pero siguen este patrón:

\begin{align} a^2 + 2ab + b^2 - x^2 +2xy - y^2 &= (a^2 + 2ab + b^2) - (x^2 -2xy + y^2) \\ &= (a+b)^2 - (x -y)^2 \\ &= (a+b + x -y)(a+b -x + y). \end{align}

Suma o diferencia de cubos

Una representación visual de la factorización de los cubos usando volúmenes. Por una suma de cubos, simplemente sustituyendo z=-y.

También hay fórmulas para la suma o la resta de dos términos elevados al cubo:

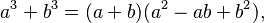
Suma de cubos: $a^3 + b^3 = (a + b)(a^2 - ab + b^2),\,\!$
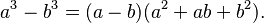
Diferencia de cubos: $a^3 - b^3 = (a - b)(a^2 + ab + b^2).\,\!$

Expansiones binomiales

Una ilustración visual de la identidad (a + b)² = a² + 2ab + b²

El teorema del binomio nos muestra patrones de coeficientes que nos ayudan a reconocer factorizaciones cuando un polinomio es la potencia de un binomio.

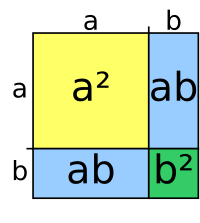
Trinomio cuadrado perfecto: Son polinomios de segundo grado que se factorizan así:

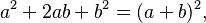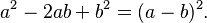
: $a^2 + 2ab + b^2 = (a + b)^2,\,\!$ : $a^2 - 2ab + b^2 = (a - b)^2.\,\!$

Cubo perfecto: Algunos polinomios cúbicos se factorizan así:

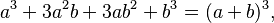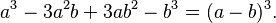
: $a^3 + 3a^2b + 3ab^2 + b^3 = (a+b)^3,$ : $a^3 - 3a^2b + 3ab^2 - b^3 = (a-b)^3.$

Los números que acompañan a las letras en estas expansiones (los coeficientes) se pueden encontrar en el triángulo de Pascal.

Uso de fórmulas de raíces del polinomio

Cualquier polinomio de segundo grado (de la forma 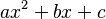$ax^2+bx+c$ ) se puede factorizar usando la fórmula cuadrática. Esta fórmula nos da las dos "raíces" (los valores de x que hacen que el polinomio sea cero), y con ellas podemos factorizar el polinomio:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^2 + bx + c = a(x - \alpha)(x - \beta)

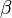donde $\alpha$ y $\beta$ son las dos raíces que se encuentran con la fórmula cuadrática.

Existen fórmulas similares para polinomios de tercer grado (cúbicas) y cuarto grado (cuárticas). Sin embargo, para polinomios de grados más altos, no hay fórmulas generales que usen solo operaciones básicas y raíces, como lo explica el teorema de Abel-Ruffini.

Factorización de matrices

Artículo principal: Factorización de matrices

En el mundo de las matrices, la factorización significa descomponer una matriz grande en la multiplicación de matrices más pequeñas. Hay diferentes tipos de factorizaciones de matrices, y cada una se usa para resolver problemas específicos en áreas como la informática o la ingeniería.

Factorización de potencias

Para factorizar las bases de las potencias, a menudo usamos el factor común. Por ejemplo, si queremos factorizar el número 24 y expresarlo usando potencias, hacemos lo siguiente:

\begin{array}{r|l} 24 & 2 \\ 12 & 2 \\ 6 & 2 \\ 3 & 3 \\ 1 & \end{array}

24 = 2^3 \cdot 3 \,

Así, 24 se puede escribir como 2 elevado a la 3 (2x2x2) multiplicado por 3.

Véase también

En inglés: Factorization Facts for Kids

Productos notables
Factorización de enteros
Factorización de matrices

Obtenido de «https://ninos.kiddle.co/index.php?title=Factorización&oldid=4961391»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Factorización para Niños. Enciclopedia Kiddle.