Fracción algebraica para niños

Una fracción algebraica es como una fracción normal que conoces, pero en lugar de tener solo números, tiene expresiones con letras y números, llamadas expresiones algebraicas. Imagina que tienes una división donde tanto la parte de arriba (el numerador) como la de abajo (el denominador) son expresiones con letras como x o y.

Por ejemplo, 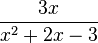es una fracción algebraica. Otro ejemplo es 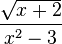. Las fracciones algebraicas siguen las mismas reglas que las fracciones que ya conoces.

Una fracción racional es un tipo especial de fracción algebraica. En este caso, tanto el numerador como el denominador son polinomios. Un polinomio es una expresión algebraica donde las letras solo tienen exponentes enteros positivos (como x², x³, etc.) y no están dentro de raíces o divisiones.

Así, 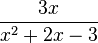es una fracción racional porque tanto 3x como x² + 2x - 3 son polinomios. Sin embargo, 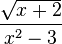no es una fracción racional, porque el numerador tiene una raíz cuadrada, lo que no es un polinomio.

¿Qué partes tiene una fracción algebraica?

En una fracción algebraica, la expresión de arriba se llama numerador y la expresión de abajo se llama denominador. Juntos, el numerador y el denominador se conocen como los términos de la fracción.

Tipos de fracciones algebraicas

Existen diferentes tipos de fracciones algebraicas:

• Una fracción compuesta es aquella donde el numerador, el denominador, o ambos, contienen otra fracción.
• Una fracción simple es lo contrario: no tiene ninguna fracción dentro de su numerador o denominador.
• Una fracción está en términos mínimos cuando el único número que puede dividir tanto al numerador como al denominador de forma exacta es el 1. Es como simplificar una fracción hasta que ya no se puede más.

Expresiones relacionadas

• Una expresión integral es una expresión que no está escrita como fracción. Por ejemplo, 5x es una expresión integral. Siempre puedes escribir una expresión integral como fracción si le pones un 1 como denominador (por ejemplo, 5x se puede escribir como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{5x}{1} ).
• Una expresión mixta es una combinación de una o más expresiones integrales y una o más fracciones. Por ejemplo, x + es una expresión mixta.

Fracciones racionales: Más a fondo

Como ya sabes, las fracciones racionales son aquellas donde el numerador y el denominador son polinomios. También se les llama a veces expresiones racionales.

Fracciones racionales propias e impropias

Las fracciones racionales pueden ser de dos tipos:

• Una fracción racional es propia si el grado (el exponente más alto) del polinomio en el numerador es menor que el grado del polinomio en el denominador. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{2x}{x^2-1} es propia, porque el grado de 2x es 1 y el grado de x² - 1 es 2.
• Una fracción racional es impropia si el grado del numerador es igual o mayor que el grado del denominador. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x^3+x^2+1}{x^2-5x+6} es impropia, porque el grado del numerador es 3 y el del denominador es 2.

Cualquier fracción racional impropia se puede reescribir como la suma de un polinomio (que puede ser solo un número) y una fracción racional propia. Por ejemplo:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x^3+x^2+1}{x^2-5x+6} = (x+6) + \frac{24x-35}{x^2-5x+6}

Aquí, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{24x-35}{x^2-5x+6} es una fracción racional propia.

Cuando sumas dos fracciones racionales propias, el resultado siempre será otra fracción racional propia.

Descomposición en fracciones simples

El proceso contrario a sumar fracciones es la descomposición en fracciones simples. Esto significa tomar una fracción racional propia y expresarla como la suma de dos o más fracciones más sencillas. Por ejemplo:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{2x}{x^2-1} = \frac{1}{x-1} + \frac{1}{x+1}

Las fracciones Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{x-1} y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{x+1} se llaman fracciones parciales.

Fracciones irracionales

Una fracción irracional es aquella que tiene una variable (una letra) dentro de una raíz o elevada a un exponente que es una fracción (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^{1/2} , que es lo mismo que 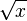). Un ejemplo de fracción irracional es:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x^{1/2} - \tfrac13 a}{x^{1/3} - x^{1/2}}

El proceso de convertir una fracción irracional en una fracción racional se llama racionalización. Esto se hace para que la expresión sea más fácil de manejar. Si una fracción irracional tiene raíces simples, puedes racionalizarla encontrando el mínimo común múltiplo de los índices de las raíces y haciendo un cambio de variable. Por ejemplo, en el ejemplo anterior, el mínimo común múltiplo de los exponentes fraccionarios (1/2 y 1/3) es 6. Si sustituimos , la fracción se convierte en:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{z^3 - \tfrac13 a}{z^2 - z^3}

Esta nueva expresión ya no tiene raíces y es más fácil de trabajar.

Véase también

En inglés: Algebraic fraction Facts for Kids